In this article, we will discuss a mathematical riddle that  seems impossible even if you know the answer
seems impossible even if you know the answer . It is better known as the 100 prisoners problem.
. It is better known as the 100 prisoners problem.
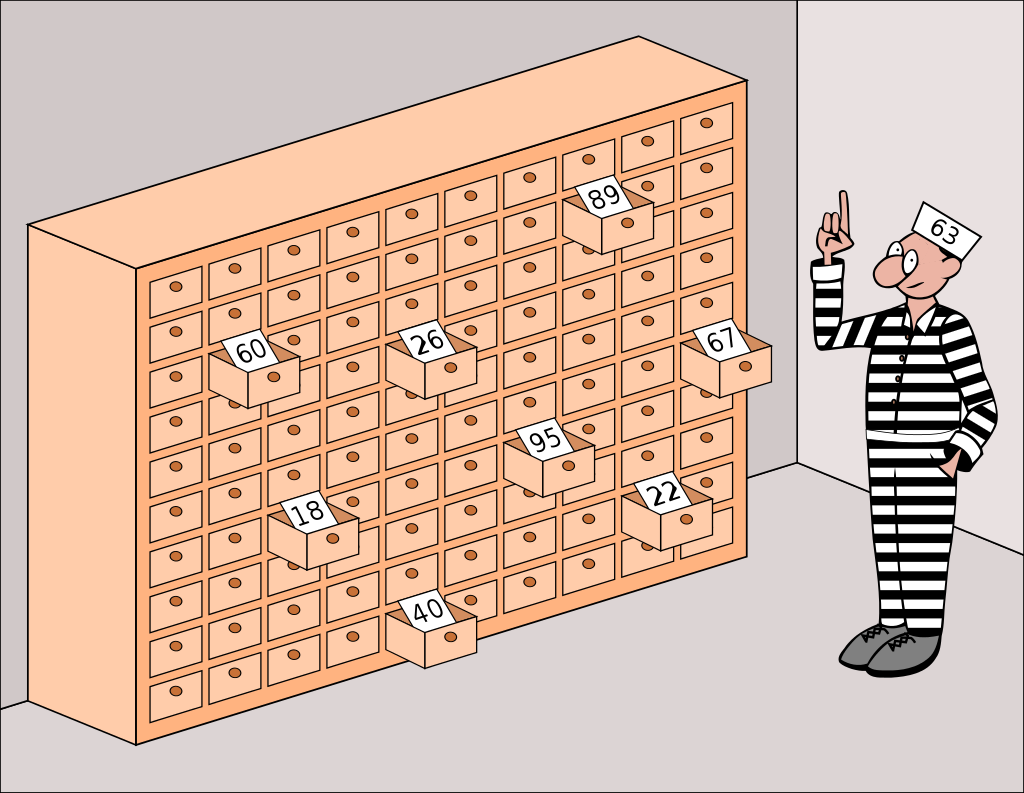
The 100 prisoners problem is a famous problem in probability theory and combinatorics. It has grown in popularity since 2003, because of its elegant and surprisingly efficient solution. Consider 100 prisoners, who all wear a hat with a different number from 1 up to 100. Each prisoner knows the number on their hat. In a room at the prison, we have a cupboard with 100 drawers, in which we randomly put the numbers 1 up to 100. Now, the prisoners enter the room, one after the other. Each prisoner may open 50 drawers in any order, but the drawers are closed afterward. If every prisoner finds their slip of paper in one of the drawers, all prisoners are pardoned. If just one prisoner does not find their slip of paper, all prisoners will be sentenced to death. Before the first prisoner enters the room, however, the prisoners may discuss a strategy. But, they may not communicate once the first prisoner enters to look in the drawers. What is the best strategy the prisoners can follow?

Unlikely to be pardoned?
At first glance, it seems quite unrealistic that the prisoners can come up with a good strategy. The most likely thing to happen would be for every prisoner to choose 50 drawers randomly. This means that each prisoner would have a probability of 50% to find their own slip of paper. With two prisoners, if both select at random, each one will succeed with a probability of 50%, so for two prisoners, it is 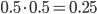 (They will succeed one time in four). Therefore, all 100 prisoners would have a combined probability of
(They will succeed one time in four). Therefore, all 100 prisoners would have a combined probability of
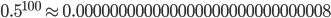
to be pardoned. You can imagine how small this number is, and therefore it seems that the prisoners don't stand a chance. However, there actually does exist a strategy that offers the prisoners a probability of success of more than 30%! Creativity and mathematics can give very surprising solutions. The key idea is that each prisoner should use the information from the drawers they have already opened to choose which drawer to open next!
Let's see how this strategy works. Each prisoner has a known number between 1 and 100. When the prisoner enters the room they start by opening the drawer corresponding to their number. The prisoner with number 30 will open the 30th drawer. If the prisoner finds their own slip of paper in the drawer, they are done. Otherwise, they find another slip of paper in the drawer and they open the drawer with that specific number. They repeat these steps until they have found their own slip of paper, or until they have opened 50 drawers.
Lets see how this works in an example. Suppose the prisoner with number 30 enters the room. They start by opening the 30th drawer and find number 2 in it, then they open the 2nd drawer to find number 79 in it. Which is the next drawer they will open? In the table below we show the first 8 steps. At some point, the prisoner may find number 30, or open 50 drawers without finding it. In the first scenario, there is some hope for all of them to be pardoned, in the second scenario, all prisoners are sentenced to death.
| Drawer opened | 30 | 2 | 79 | 1 | 15 | 49 | 33 | 62 |
| Number in drawer | 2 | 79 | 1 | 15 | 49 | 33 | 62 | 11 |
We claim that if the prisoners follow this strategy then they will be pardoned with a probability higher than 31%!
Unbelievable answer
The important question to ask is: Why does this strategy work? Note that every drawer contains one slip of paper and that these slips are unique. So either the number is in the correct drawer, or it points to another drawer. There is only one slip of paper pointing to each drawer (and only one way to get to any drawer). This means that the drawers will form circular chains. In the example above, if we keep going, at some point we will definitely find a drawer with the original number in it! Why is this? Take some time to investigate this question.
| 30 | 2 | 79 | 1 | 15 | 49 | 33 | 62 | 3 | 99 | 98 |
| 2 | 79 | 1 | 15 | 49 | 33 | 62 | 3 | 99 | 98 | 30 |
If we keep going, at some point we will definitely find a drawer with the original number in it!
A drawer can only be part of one chain, since there is only one number leading to a drawer, and one number leading out of any drawer. Some chains might be as short as one or two drawers (as in the example below), but they can also be longer.
| 5 |
| 5 |
| 45 | 4 |
| 4 | 45 |
We could also have one chain of length 100, where each number points to its subsequent number. Note that since the prisoner starts with the drawers of their own number, they are on the chain that contains their slip of paper. If they follow the chain, they are guaranteed to end up at their number eventually. The only question remaining is if they can find their slip of paper before fifty boxes are opened!
Chain Length
Here is a second important step, to translate the original question to a question about these chains of drawers. Can you think which property these chains should satisfy in order for all prisoners to be able to find their number within 50 steps?
For everyone to succeed, the maximum chain length needs to be less than fifty drawers long. If a chain is longer than fifty drawers, then those who have their slip of paper in that chain will fail. Think about this for a second. If we have a chain of length 51 for instance, the prisoner's slip will always be in the last box of that chain, since you start with the box with your own number on it. In this case, that would be box 51, which you can't open in 50 tries. Note that there can only be one chain of length larger than 50 since for a chain of 51 there can only be 49 drawers remaining for a second chain.
A mathematical surprise
After you've convinced yourself that, for success, the maximum chain length should be less than or equal to 50, and there can only be one chain in any set that has a chain greater than fifty, we can calculate the probability of success (thus: the prisoners being set free) as:
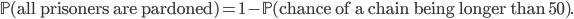
So, what we need to work out is the probability that a long chain exists. Consider a chain of length 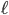 , we need to find in how many ways such a chain can be constructed. Consider a concrete example below for
, we need to find in how many ways such a chain can be constructed. Consider a concrete example below for  . In total the chain will contain
. In total the chain will contain 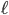 different numbers out of the 100 numbers. Suppose these are the 11 numbers shown below.
different numbers out of the 100 numbers. Suppose these are the 11 numbers shown below.
| 30 | 2 | 79 | 1 | 15 | 49 | 33 | 62 | 3 | 99 | 98 |
| ? | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
But, these numbers don't always form a chain of length 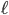 . For example, if drawer 49 has number 49 in it then the chain breaks down.
. For example, if drawer 49 has number 49 in it then the chain breaks down.
| 30 | 2 | 79 | 1 | 15 | 49 | 33 | 62 | 3 | 99 | 98 |
| 2 | 79 | 1 | 15 | 33 | 49 | 62 | 3 | 99 | 98 | 30 |
So in order to have a chain of length 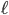 no drawers should contain the number of the drawer. Moreover, there should exist no shorter chains in the chain, like in the example below.
no drawers should contain the number of the drawer. Moreover, there should exist no shorter chains in the chain, like in the example below.
| 30 | 2 | 79 | 1 | 15 | 49 | 33 | 62 | 3 | 99 | 98 |
| 2 | 79 | 1 | 30 | 49 | 33 | 62 | 3 | 99 | 98 | 15 |
Drawers 30, 2, 79 and 1 form a chain of length 4.
Hence we want to know how many chains of length 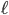 we can make using $\ell$ numbers. Some drawer will contain the first number, in our example number 30. Say this is drawer 62.
we can make using $\ell$ numbers. Some drawer will contain the first number, in our example number 30. Say this is drawer 62.
| 30 | 2 | 79 | 1 | 15 | 49 | 33 | 62 | 3 | 99 | 98 |
| ? | ? | ? | ? | ? | ? | ? | 30 | ? | ? | ? |
Drawers 30, 2, 79 and 1 form a chain of length 4.
We want to fill all other boxes with numbers so that we create a chain of length 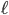 , in the example of length 11. Can you find a way to do this? We claim there are in total
, in the example of length 11. Can you find a way to do this? We claim there are in total
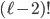
ways to do this. Do you see why?
At the beginning, we said that drawer 62 contained the number 30, but any of the 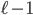 (not drawer 30) drawers could contain the number 30. Hence in total, there are
(not drawer 30) drawers could contain the number 30. Hence in total, there are
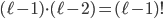
ways to construct a chain of length $\ell$ with $\ell$ numbers. But this argument holds if we have 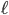 specific numbers, but we have 100 numbers from which we choose
specific numbers, but we have 100 numbers from which we choose 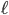 . Hence we need to know in how many ways we can choose
. Hence we need to know in how many ways we can choose 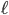 numbers from the 100 available ones. This can be done in
numbers from the 100 available ones. This can be done in
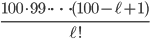
ways. Do you see why this is the case? Don't worry if you don't see it, you can go further and think about it later.
There are in total 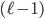 ! ways to organize the numbers we picked. The remaining numbers can be arranged in
! ways to organize the numbers we picked. The remaining numbers can be arranged in 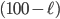 ! ways, these will also form chains of various lengths. When we combine these, we find that the number of allocations of numbers to drawers that contain a chain of exactly length
! ways, these will also form chains of various lengths. When we combine these, we find that the number of allocations of numbers to drawers that contain a chain of exactly length 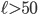 is:
is:
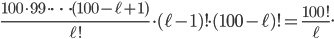
Pause a moment to think about this. Since there are a total of 100! possible ways of arranging the numbers, the probability there is a chain of length 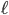 is just
is just 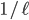 . Thus we find that the probability of success of this strategy is equal to
. Thus we find that the probability of success of this strategy is equal to
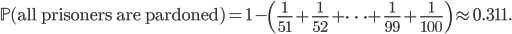
Thus, with this strategy, the prisoners approximately have a 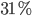 chance of being set free!
chance of being set free!
A Spy
Let's consider the same puzzle, but now add a spy, who is able to sneak into the room beforehand and examine the locations of all the slips of paper. The spy can (optionally) swap just two of the slips, but is not able to communicate what change he made. What strategy should the spy adopt to improve the prisoners' chance of escape?
In this article, we have seen that, even though it may seem impossible, we can find a solution to a riddle  that seems impossible even when we know the answer
that seems impossible even when we know the answer . We have learned that, when we think outside the box and use some simple mathematics, we can solve problems that may at first sight seem unsolvable.
. We have learned that, when we think outside the box and use some simple mathematics, we can solve problems that may at first sight seem unsolvable.