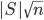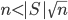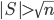It is possible to avoid large homogeneous substructures in general networks, but a conjecture of Erdős and Hajnal from 1989 says that forbidding any specific substructure results in existence of a very large homogeneous one! In this article you will have a look into one of the most fascinating problems in modern graph theory.
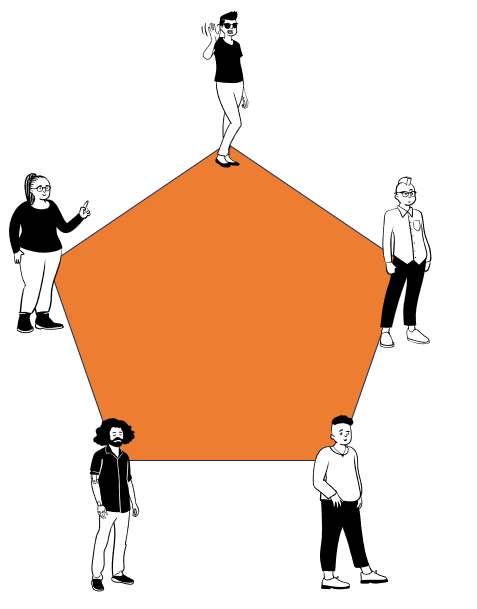
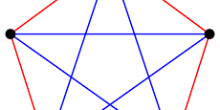
If you see six people when you enter a class, it might be difficult to guess their personalities, but there is an amazing thing you can be sure of (mathematically prove): there are three of them who either all know each other, or who have never met. On the contrary, if there are only five people, there is a chance that you might fail to find such a triple: consider five people sitting around a circular table in a way that everybody knows only their two neighbors. Whoever three people you choose there will always be two people who know each other and two people who don't know each other, never all three.
Figure 1: Five people sitting around a circular table.
Why does this argument fail when you have six people sitting around a circular table? Think about this for a moment.
This simple observation due to Frank Ramsey in 1930 was the first step in mathematicians building a great theory on it ever since -- nowadays called Ramsey theory. It mainly concerns the structures emerging as the group gets larger. People in a class who may (or may not) have met before can be represented as a network of points that may (or may not) be linked to each other by an edge. There is a whole branch of mathematics that represents mathematical problems about networks in that way, called graph theory, and Ramsey theory is a subfield of graph theory.
Let us call a group of people homogeneous if either all know each other, or who have never met. Suppose instead of a group of three, you want to find a homogeneous group of size four. You can easily convince yourself that if, for instance, there are 10000 people in the class, this should be an easy task. But, what about the minimum size of the class in order to guarantee existence of such four people? The following example in the figure below shows you might fail if there are only 17 people:
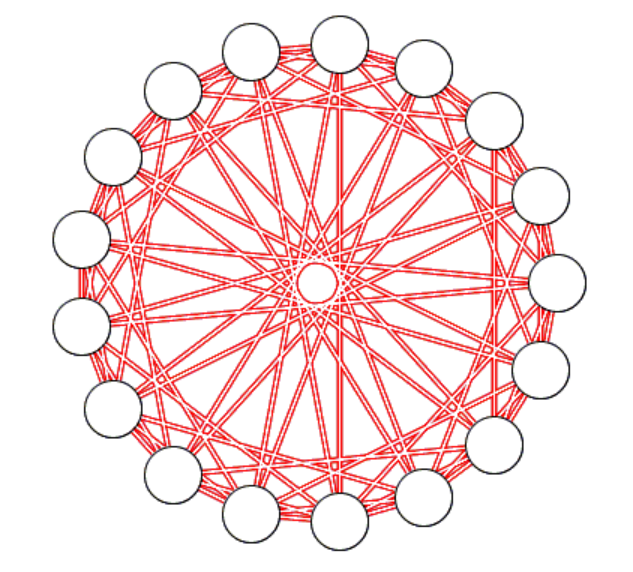
Figure 2: An example of a graph on 17 vertices with no homogeneous set of size four
Indeed, it is the best example! It can be shown that one can always find a homogeneous group of size four in every group of 18 people.
Ready to be surprised? Mathematicians have no answer (yet) for the next obvious question:
Question: What is the minimum number of people to guarantee the existence of a homogeneous group of size five?
The question above is just one example of problems in graph theory which are innocent-looking but enormously difficult! Mathematicians are only able to establish that the answer should be a number between 43 and 48. How can this problem be not fully answered? I can hear you saying a computer would do the job, but it turns out that we need more than 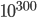 computations, which is quite beyond today's computer's abilities.
computations, which is quite beyond today's computer's abilities.
What about the asymptotics?
Let us start formalizing the concepts. In graph theory language, homogeneous groups correspond to substructures in graphs which are either all connected or all disconnected, respectively called cliques and independent sets. Letting 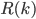 be the minimum integer
be the minimum integer  such that every graph on
such that every graph on  vertices has a homogeneous substructure of size
vertices has a homogeneous substructure of size  , the previous discussion is mathematically equivalent to saying that
, the previous discussion is mathematically equivalent to saying that 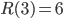 and
and 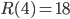 . Recall that what we could only say about
. Recall that what we could only say about 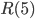 was that
was that 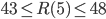 , so it seems there is no hope for
, so it seems there is no hope for 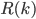 when
when 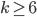 , desperate! But, mathematicians never give up.
, desperate! But, mathematicians never give up.
If something is quite difficult to determine exactly, it is natural to try to understand what it looks like by giving some good upper and lower bounds. The term asymptotic behavior for a function 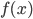 informally means the categorization of
informally means the categorization of 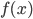 when
when 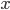 grows towards infinity in terms of well-understood functions such as
grows towards infinity in terms of well-understood functions such as 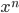 or
or 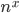 . For the case of our problem, the behavior of
. For the case of our problem, the behavior of 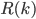 when
when 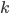 gets larger, the famous mathematician Paul Erdős, as the founder of the probabilistic method, used a probabilistic argument to show that
gets larger, the famous mathematician Paul Erdős, as the founder of the probabilistic method, used a probabilistic argument to show that 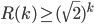 . For the upper bound, Ramsey himself proved that
. For the upper bound, Ramsey himself proved that 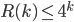 by using a mathematical method called induction, still a huge gap!
by using a mathematical method called induction, still a huge gap!
The exact asymptotics of 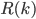 -- whether
-- whether 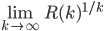 exists or not -- is still one of the biggest open problems in Ramsey theory, but now we are moving to the part in which we discuss another aspect of homogeneous structures. You can and look at proofs of aforementioned upper and lower bounds at the great reference
exists or not -- is still one of the biggest open problems in Ramsey theory, but now we are moving to the part in which we discuss another aspect of homogeneous structures. You can and look at proofs of aforementioned upper and lower bounds at the great reference  Proofs from the book, Chapter 45: Probability makes counting (sometimes) easy
Proofs from the book, Chapter 45: Probability makes counting (sometimes) easy . Also you can read Nicos Starreveld's article about the latest breakthrough about the upper bound for
. Also you can read Nicos Starreveld's article about the latest breakthrough about the upper bound for 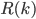 and further discussion.
and further discussion.
Homogeneous substructures are unavoidable, but how large can they be?
Let us interpret the upper and lower bounds for 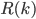 from another perspective:
from another perspective: 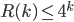 shows that every graph on
shows that every graph on  vertices has a homogeneous substructure of size
vertices has a homogeneous substructure of size 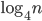 . On the other hand, Erdős' result
. On the other hand, Erdős' result 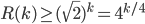 says that in an
says that in an  -vertex graph, you can avoid homogeneous substructures of size
-vertex graph, you can avoid homogeneous substructures of size 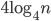 . The main message from these two facts can be summarized as follows:
. The main message from these two facts can be summarized as follows:
- In an arbitrary graph, logarithmic sized homogeneous substructures are unavoidable.
- There are graphs whose largest homogeneous substructure has logarithmic size.
Erdős and his collaborator Andras Hajnal asked a question in a paper published in 1989 that is still quite open: Take any substructure you want, say 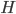 . If a graph does not have a part that exactly looks like
. If a graph does not have a part that exactly looks like 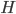 in terms of edges and non-edges, it is called
in terms of edges and non-edges, it is called 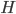 -free. They conjectured that any
-free. They conjectured that any 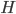 -free graph has to have a polynomial size homogeneous substructure -- rather than only logarithmic size you would see in an arbitrary graph (note that for any fixed positive numbers
-free graph has to have a polynomial size homogeneous substructure -- rather than only logarithmic size you would see in an arbitrary graph (note that for any fixed positive numbers  and
and 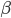 ,
, 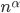 becomes much larger than
becomes much larger than 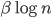 when
when  gets larger.).
gets larger.).
Erdős-Hajnal conjecture
For every graph 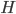 , there exists a constant
, there exists a constant 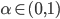 such that every
such that every 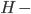 free graph
free graph  on
on  vertices has a homogeneous substructure of size
vertices has a homogeneous substructure of size 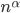 .
.
Shall we believe in this conjecture?
At the first glance, it might not be intuitive why forbidding a substructure can drastically change the size of the largest homogeneous substructure in a graph compared to arbitrary graphs of the same size, but, of course, there are (mathematical) reasons for it. Maybe it is best to think about it first through an example. Let  be a graph that contains three vertices and two edges, i.e. a substructure looks like a path of two edges, depicted in Figure 3 below.
be a graph that contains three vertices and two edges, i.e. a substructure looks like a path of two edges, depicted in Figure 3 below.

Figure 3: A path graph  with two edges.
with two edges.
Can we describe 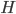 -free graphs? Let
-free graphs? Let  be a
be a 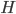 -free graph. Now we will try to understand how this affects the structure of
-free graph. Now we will try to understand how this affects the structure of  . Consider a vertex
. Consider a vertex 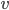 in
in  which has at least two other neighbors (vertices adjacent to
which has at least two other neighbors (vertices adjacent to 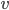 through a link). Call them as
through a link). Call them as  , depicted in Figure 4 below.
, depicted in Figure 4 below.
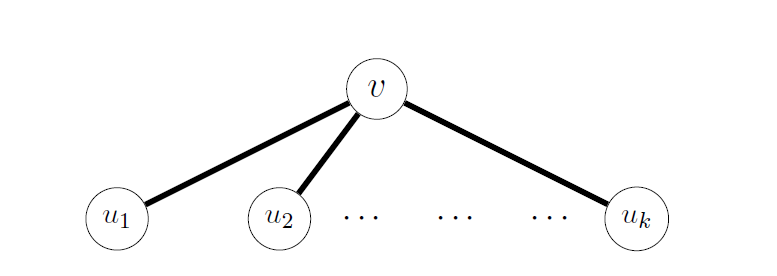
Figure 4: The vertex  and its neighbors.
and its neighbors.
If  and
and  are not linked for some
are not linked for some 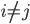 , then observe that
, then observe that 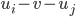 would be the same graph with
would be the same graph with  (see Figure 5), a contradiction.
(see Figure 5), a contradiction.
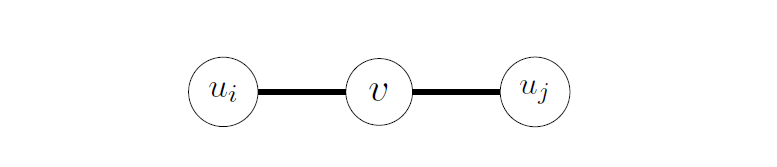
Figure 5: The vertex 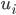 and
and 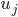 are not connected, then
are not connected, then  contains
contains 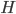 .
.
Therefore, all the neighbors of 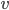 should be connected to each other, and this is true for any vertex with at least two neighbors. If you think about it for a few more seconds, you can conclude that
should be connected to each other, and this is true for any vertex with at least two neighbors. If you think about it for a few more seconds, you can conclude that  should be a disjoint union of parts such that each part is a clique -- all vertices should be linked to each other within the substructure (treat a single vertex as a clique as well). Suppose
should be a disjoint union of parts such that each part is a clique -- all vertices should be linked to each other within the substructure (treat a single vertex as a clique as well). Suppose  consists of
consists of 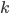 many cliques. Observe that the largest part has at least
many cliques. Observe that the largest part has at least 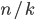 vertices, so we find a homogeneous structure of size
vertices, so we find a homogeneous structure of size 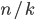 . On the other hand, we can choose one vertex from each part, they form again a homogeneous substructure because they are all disconnected. As a result, we can find a homogeneous substructure of size
. On the other hand, we can choose one vertex from each part, they form again a homogeneous substructure because they are all disconnected. As a result, we can find a homogeneous substructure of size 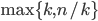 . Since
. Since 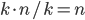 , either
, either 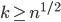 or
or 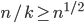 , so
, so 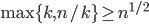 . So, we proved the conjecture when
. So, we proved the conjecture when 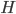 is path graph consisting of two edges! One case is done among infinitely many graphs. You can try to prove one more case yourself.
is path graph consisting of two edges! One case is done among infinitely many graphs. You can try to prove one more case yourself.
Exercise: Let 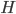 be the triangle graph, as depicted in Figure 6. Prove that every
be the triangle graph, as depicted in Figure 6. Prove that every 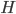 -free graph on
-free graph on  vertices has a homogeneous set of size
vertices has a homogeneous set of size 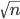 .
.
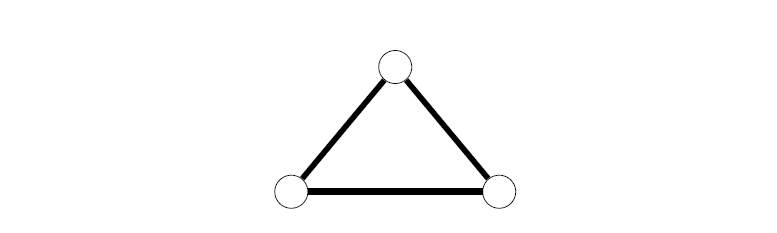
Figure 6: A triangle graph  consisting of three vertices which are all connected.
consisting of three vertices which are all connected.
Solution: Let  be a triangle-free graph on
be a triangle-free graph on  vertices. We will prove that
vertices. We will prove that  has an independent set of size
has an independent set of size 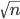 .
.
- Suppose there exists a vertex of at least
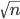 neighbors. Then, any two such neighbors …
neighbors. Then, any two such neighbors …
- Suppose all the vertices have less than
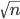 neighbors. Consider the largest independent set
neighbors. Consider the largest independent set 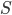 , then …
, then …
You can see that the conjecture is so strong because it is about any graph 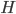 . Desperately, since Erdős and Hajnal, there has been no significant progress with the exception examining some special cases of the graph
. Desperately, since Erdős and Hajnal, there has been no significant progress with the exception examining some special cases of the graph 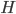 , just like we did. However, even the case of
, just like we did. However, even the case of 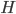 being a path of four edges (see Figure 7) is still unknown!
being a path of four edges (see Figure 7) is still unknown!

Figure 7: A path graph 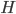 with four edges.
with four edges.
You can say that even if we could solve this case, it would not mean a huge step towards the general solution of the conjecture (because there are infinitely many graphs). You would be right, but as mathematician we do what we can do!
You can look at the papers listed at the end of this article to have an idea about the recent progress towards the conjecture, which makes mathematicians more optimistic about a proof in the near future. But who knows, maybe we still need to wait for a long time...
Further reading
- The Erdős-Hajnal Conjecture for Bull-free Graphs by Maria Chudnovsky and Shmuel Safra.
- The Erdős-Hajnal Conjecture by Maria Chudnovsky.
- Erdős-Hajnal for graphs with no 5-hole by Maria Chudnovsky, Alex Scott, Paul Seymour, and Sophie Spirkl.
- Towards the Erdős-Hajnal conjecture for $P_5$-free graphs by Pablo Blanco and Matia Bucic.
- Induced subgraph density I: A loglog step towards Erdős-Hajnal by Matia Bucic, Tung Nguyen, Alex Scott, and Paul Seymour.