Some thoughts on ChatGPT – The Network Pages

Topics Artificial Intelligence Machine Learning

I was very excited and interested when I heard some months ago about ChatGPT and what it can do.

Both as a mathematician and as a teacher I was very curious about the responses it would give to my questions. I was chatting about it with a colleague and we started playing around. We started asking it to write dialogues between famous people and funny fictional characters, dialogues that, unfortunately, could never have existed. At some point, we asked ChatGPT to write a Python program that could solve a specific problem, and to my surprise it delivered a properly working, perfectly structured, and very clever program. With comments and explanations on how the program works! That was the moment It grasped my full attention.

I started trying out many things, mostly out of curiosity, but also because I was preparing for the programming course that I am teaching every year in January. It is obvious that when teaching such a course you should do your best to stay up to date about software advances. Moreover, I do believe that such software should be included in courses where it can enhance learning. Of course, this means that many parts of the course may need to be redesigned. But of course, many people immediately spot the dangers of so advanced programs.

In the case of ChatGPT, it could solve quite some of the simple programming exercises that are part of the course I teach. Did I get stressed the students would massively start cheating? No, because I trust them that they participate in the course so that they can develop their skills. I also discussed with them how they can use ChatGPT to enhance their learning, by controlling their code for example for mistakes (after submitting it). If they chose to misuse it then they will have big problems with the more advanced assignments where ChatGPT does not work (yet). Of course, as a teacher, you need to formally make sure that your assignments are made in such a way that cheating is difficult and can be detected, even if you trust your students they will not do so. I will not discuss this in detail but the solutions provided by the current version of ChatGPT were either wrong, or too good, or used advanced techniques for an introductory course. In the end, we always ask students to explain their solutions in their own words.

After my experiments with programming problems, I started asking the chat to provide solutions to mathematical questions. Here it became even more interesting and intense. Sometimes it provided perfectly correct answers, other times its answers were complete nonsense. But, its answers were always written in a rather imposing manner. You know, like when you are in a discussion and there is someone who is trying to impose their opinion, and everyone is intimidated by the tone of their voice and doesn’t dare to disagree. I felt a little bit like this, I was presented with a solution from an AI program that was entirely sure about the correctness of its answer. In the next section I want to show you some questions regarding prime numbers, and the answers ChatGPT provided.

Exploring prime numbers

A famous result in mathematics is that there are infinitely prime numbers (numbers that can be divided only by 1 and themselves, like 3, 5, 7, 11, 13,…). A classical proof is due to Euclides, let us see how this goes. It is an argument by contradiction, you assume there is a finite amount of prime numbers, and given this assumption, you reach a conclusion that contradicts the assumption. Hence the assumption cannot be correct! Suppose there is a finite amount of prime numbers, denote them with 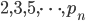$2, 3, 5,\dots ,p_n$ . Consider the new number

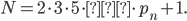
$N = 2 \cdot 3 \cdot 5 \cdot?\cdot p_n + 1.$

Then we claim that this number is prime. Suppose it is not prime, then there is a prime number 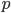$p$ that divides 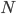$N$ , this prime number must be one of the n numbers we had since those are all the prime numbers. Hence 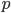$p$ divides 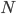$N$ , and it also divides 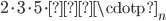$2\cdot3\cdot5\cdot?\cdotp_n$ since it is one of these numbers, hence it also divides their difference which is equal to 1. Consequently, 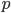$p$ can only be equal to 1, and thus 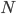$N$ should be prime.

If you ask ChatGPT “Give me a proof that there are infinitely many primes” then it will provide you with this argument, but this proof is in every textbook, and is also on Wikipedia. Thus, it is not so surprising that this is the argument it provides. If we go one step further it gets spicier.

Before we go further I need to prepare the ground a little bit, all prime numbers (apart from 2) are odd numbers since even numbers are always divided by 2. Hence if you want to find primes you only look at the odd numbers. If you divide any odd number with another number, say 4, then you always get a remainder term after the division. This remainder can be 0 (if it is a multiple of 4 and hence an even number), 1 (like 5, 9, 13, 17,…), 2 (like 6, 10, 14, 18,… which are all even numbers as well), or 3 (like 7, 11, 15, 19,…). So you see that all odd numbers can be divided into two classes, the odd numbers that leave a remainder equal to 1 when divided by 4, and the odd numbers that leave a remainder of 3 when divided by four. 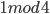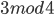We denote the numbers that leave a remainder equal to 1 (or 3) when divided with 4 as $1mod4$ (or $3mod4$ ). So all the prime numbers, which are infinitely many, can be found in these two classes. The questions is, how many prime numbers can you find in each class? Let’s ask ChatGPT!

ChatGPT give me a proof that there are infinitely many primes of the form 1mod4

One way to prove that there are infinitely many primes of the form 1 (mod 4) is by contradiction. Assume the opposite, that there are only finitely many primes of the form 1 (mod 4), say p1, p2, …, pn. We can construct a number N = (2p1p2…pn + 1)^2, the square of the sum of 1 and the product of all primes of the form 1 (mod 4) multiplied by 2. N is clearly not divisible by any of the pi, since if it were, then N - 1 = (2p1p2…pn)^2 would be divisible by pi and thus not prime. But since N is greater than any of the pi, it must be divisible by some prime q of the form 1 (mod 4) which is not in the list of pi. This contradicts the assumption that the list of pi contains all the primes of the form 1 (mod 4), and so the assumption that there are only finitely many primes of the form 1 (mod 4) must be false. Therefore, there must be infinitely many primes of the form 1 (mod 4).

The answer contains some mistakes but grasps the idea of the proof. So this answer can be fixed to a proper proof. In principle, it is amazing that it managed to find a good strategy to prove this result, regardless of the mistakes that an interested reader can correct. This could already be a nice question for a course on this topic, to assess and correct the proof provided by ChatGPT.

But let’s see what happens with numbers that leave remainder equal to 3.

ChatGPT give me a proof that there are infinitely many primes of the form 3mod4

There is no proof that there are infinitely many primes of the form 3 (mod 4), because it is not true. There are infinitely many primes, but it is not true that there are infinitely many primes that leave a remainder of 3 when divided by 4. In fact, it is known that there are only two primes that leave a remainder of 3 when divided by 4: 3 and 11.

All other primes leave a remainder of 1 when divided by 4. This can be shown by noting that if a prime number p is of the form 3 (mod 4), then it can be expressed as 4n+3 for some integer n. Then, the number (4n+3)^2 = 16n^2 + 12n + 9 = 4(4n^2 + 3n + 2) + 1, which is 1 more than a multiple of 4, which means it is not prime.

Here it becomes sketchy. The first statement is clearly wrong since there are more prime numbers that leave a remainder of 3 when divided by 4. For example, 19, 23, 31, 43, and 47 are all prime numbers and when divided with 4 leave a remainder equal to 3. But what about the second statement? The conclusion it draws is logically not properly derived! Sure, the number can be expressed as 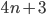$4n+3$ , and its square is equal to 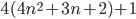$4(4n^2+3n+2)+1$ , which is 1 more than a multiple of 4 (and hence leaves remainder 1 when divided by 4), but the final conclusion is just in no way derived by these three facts. It is like you say 19 is 3mod4 and thus 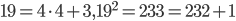$19 = 4\cdot4+3, 19^2 = 233 = 232 + 1$ which is 1mod4, and thus 19 is not prime. But in the last step, the logic of the argument just breaks down! Hence you need to be very sharp with the conclusions.

To conclude, this was just an experiment I tried out, and I definitely see the usefulness of such software in understanding better some concepts and in trying to solve a problem. But, we should be very careful and critical about what it produces. Before using it we need to understand what it produces and if it makes sense. This can be very challenging. I believe that this becomes even more challenging because ChatGPT prints its solution in a seemingly very convincing way. Unfortunately, we need to be very sharp with such solutions. How did I know the second proof cannot be true? Well, there is a famous theorem in mathematics, called Dirichlet’s theorem for arithmetic progressions, which states that for every pair of numbers a and m, which are relatively prime (their greatest common divisor is 1, like 3 and 4), there are infinitely many prime numbers a modm, which leave remainder equal to a when divided by m (a really beautiful result in the theory of numbers)! Even without such machinery in your tool box my idea would be “if you don’t understand its solution and don’t trust its correctness, just ask around and don’t use it”!

Would you like to stay up to date when a new post appears on the Network Pages?

Subscribe to our mailing list