Have you ever wondered how people with a severe visual impairment practice and understand mathematics?
In most cases when people practice mathematics they rely heavily on visual information, write down formulas and work out examples, or draw diagrams and graphs. People with a severe visual impairment, who read in braille (from here on braille readers), have to rely on other skills and use other methods to practice and understand mathematics.
In November 2021 Annemiek van Leendert defended her doctoral thesis and received the degree of doctor. The title of her thesis is Improving Reading and Comprehending Mathematical Expressions in Braille.
Her promoters and co-promoters were Prof. Dr. P. H. M. Drijvers and Dr. L. M. Doorman (Freudenthal Institute, Utrecht University) and Prof. Dr. J. van der Steen and Dr. ir. J. J. M. Pel (Erasmus Medical Center, Department of Neuroscience).
Annemiek has been (for more than thirty years) working for Royal Visio, an organization that provides care and education for people with visual impairment. Annemiek received a grant from the Dutch Research Council (NWO) to carry out her doctoral research.
In her research, Annemiek investigated how braille readers can become more proficient in reading and understanding mathematical expressions. She approached this issue from various perspectives.
First, Annemiek did research on how braille readers read and understand mathematical expressions in braille, as well as how to improve their tactile reading strategies. In addition, she looked at the professional development of mathematics teachers teaching braille readers. She developed a course for mathematics teachers where both tactile and auditory perception played an important role.
Finally, Annemiek investigated which mathematical braille notations are used in other countries (three non-European and thirteen European countries), and how specific features of these notations can help braille readers with reading and understanding mathematics.
Mathematics in Braille
Reading in Braile
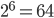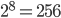Braille is a system of raised dots that allows people to read with their fingertips. A braille cell consists of six (⠿) or eight dots (⣿). We, therefore, speak of 6-dot or 8-dot braille. A dot can either be felt or not. The braille characters differ from each other in the location of the raised dots. In 6-dot and 8-dot braille it is therefore possible to create a maximum of and braille characters.
Braille readers read by moving their fingertips over the braille characters. Words, mathematical expressions, and equations are displayed in braille characters. When reading, the fingertips move from left to right over the braille characters, and each character must be read separately. This is called tactile reading. We can distinguish two braille reading techniques: the conjoint and the disjoint braille reading technique.
In conjoint reading, the index fingers move one or two braille cells from each other. In disjoint reading, the two index fingers explore different parts of the line. Disjoint reading offers more flexibility to braille readers because this technique allows them to combine and compare braille characters that are relatively far apart. This can be useful when reading mathematical expressions and the braille reader, for example, wants to know where the closing parenthesis is or what kind of expression it is.
The letters of the alphabet are depicted in the same way in 6-dot and in 8-dot braille. The letters a, b, and c, for example, are represented as ⠁(a),⠀⠃(b), and ⠉ (c). In 6-dot braille, a number sign (⠼ ) is often used to represent numbers. The numbers 1, 2, and 3 are then displayed as ⠼⠁(1), ⠼⠃(2), and ⠼⠉(3). This is not necessary for 8-dot braille because more combinations are possible. For example, the number 3 can be displayed as ⠩⠀ or as ⢉.
Words and mathematical expressions are displayed in braille characters. Due to the dimensions of the braille cells (⠿ or ⣿) only a limited number of combinations of raised dots is possible. In addition, all braille cells are in a straight line. It's not possible to place a braille character slightly higher or lower (as for example in ). Braille is, therefore, a linear notation.
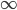In mathematics, complex symbols are often used, such as for a square root or for infinity. In braille, such symbols must be displayed in dots. That is difficult because the number of dots in a braille cell is limited.
Touching mathematics
In 6- dot Dutch mathematical braille notation, mathematical expressions resemble TeX code. An expression is written in linear tex form and then converted to braille. See the table below for some examples.
mathematical notation
linear braille notation
24 + 15 = 39 (1)
⠼⠃⠙⠀⠖⠀⠼⠁⠑⠀⠶ ⠼⠉⠊ In print: #24 + #15 = #39
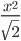(2)
⠭⠬⠼⠃⠌⠎⠟⠗⠞⠦⠼⠃⠴ In print: x^#2/sqrt(#2)
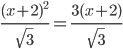(3)
⠦⠦⠭⠀⠖⠀⠼⠃⠴⠬⠼⠃⠴⠌⠎⠟⠗⠞⠦⠼⠉⠴⠀⠶⠀⠦⠼⠉⠦⠭⠀⠖⠀⠼⠃⠴⠴⠌⠎⠟⠗⠞⠦⠼⠉⠴ In print: ((x + #2)^#2)/sqrt(#3) = (#3(x + #2))/sqrt(#3)
Note: # stands for number sign (⠼).
We notice right away that there is an essential difference between the mathematical notation in print and in braille. Print readers can use the shape and positions of the symbols to understand the meaning of the expression faster and better. In a fraction, for example, the numerator and denominator are placed one above the other and separated by a line. This is not possible in braille, because braille is a linear output modality, and all braille cells are the same size.
Braille readers must read each braille character individually and one after the other in order to build an overview of the mathematical expression. This demands a lot from the working memory of the braille reader. An additional complication is that the braille characters are quite difficult to distinguish from each other. A reader with typical vision, on the other hand, can make use of the specific shape of symbols and the layout of the expression.
All over the world, different mathematical braille notations are used. In some notations, getting an overview of an expression is facilitated by announcing the structure of an expression or a part of an expression, for example, that it concerns a fraction. Then an expression of the form 'bf x^#2/sqrt(#2) ef' is used, where bf stands for beginning and ef for end of a fraction. Such kind of structure-markers are not used in the Dutch mathematical braille notation.
Annemiek has been looking for other ways to help braille readers build an overview of mathematical expressions. Her research focused on tactile reading strategies that help braille readers to better understand and use the mathematical structure of expressions and equations.
Making Mathematics Accessible
Relieve working memory
As an example, take equation (3) in Table 1. If the braille reader wants to form a picture of the equation, he/she will first read each braille character separately. The braille reader starts at the leftmost braille character and thus moves to the right over the braille characters. Only after reading the first open parenthesis after the '=' sign, the braille reader knows that it is about an equation. The question is whether the braille reader knows, after reading the whole equation, that it concerns an equation of two like fractions. This is what a reader with typical vision sees at a glance, and what helps to find the solution.
Therefore, Annemiek developed an intervention that teaches braille readers to use tactile reading strategies with a focus on the mathematical structure of expressions and equations. Annemiek's intervention is based on a number of assumptions about how braille readers can read and understand mathematical expressions and equations. In Annemiek's research the following didactic concept is central:
Didactic concept
The first step to understanding the structure of an expression or an equation is to decode, as accurately as possible, each element of the expression or equation.
The second step is to look for relationships between different parts of the expression, or equation.
Finally, the exact calculation of the expression or the solution to the equation follows.
This is elaborated in the intervention in the following way:
Intervention
For the first step, a conjoint reading style is the most suitable because this reading style is best suited for exact reading. During this exercise, the braille readers are also expected to try and build a global view of the expression or the equation.
For the second step, a disjoint reading style seems most appropriate, because it allows the braille reader to physically link and compare different parts of the expression or equation.
For the last step, that was performing the exact calculation or finding the solution, different reading styles can be used depending on the type of expression or equation, and on the experience and knowledge of the braille reader.
Figure 1 shows the finger movements (black and gray lines) while reading the expression '24 + 15 ='. In Figure 1(a), the whole process is displayed. Here you can see that the braille reader first reads the entire expression with his left and right index fingers. Then the sum is calculated by first adding the tens and then add the units together (20 + 10 = 30 and 4 + 5 = 9). The disjoint reading style (see Figure 1(c)) supports this process. In the end, both fingers are used to scan the whole expression again.
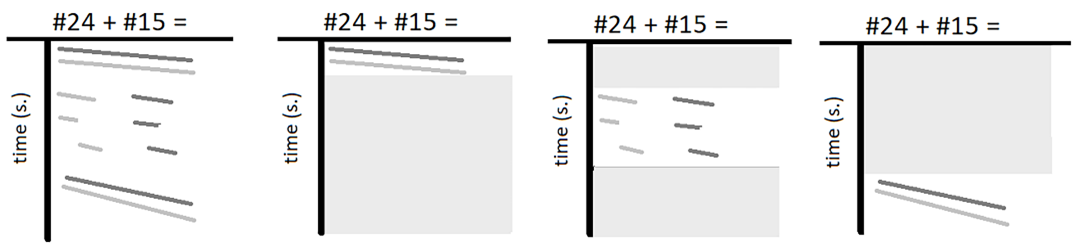
Figure 1: Schematic representation of the finger movements when reading the expression '24 + 15 =' in braille. The movements of the left and right index finger are shown in light and dark grey, respectively. (a) shows the whole reading process. (b), (c) and (d) represent the successive stages of this process.
In five steps
The intervention consists of five individual lessons of 45 minutes. Lisan Boonstra contributed to the development and implementation of this intervention. In the first lesson the focus was mainly on decoding the braille characters and on the structure of mathematical expressions. The braille readers learned how to explore the mathematical structure by touch. Think, for example, holding the opening or closing parenthesis.
In the second and third lesson, the braille readers learned to use finger movements that support understanding mathematical expressions and equations. An important strategy, for example, is to read the left and right side of an equation 'simultaneously' with disjoint reading. This makes it possible to compare the expressions to the left and right of the '=' sign. In the last two lessons the students practiced with more challenging expressions and equations to master the aforementioned techniques.
Didactical responsibility
Annemiek opens her thesis with a quote from Ignacio Estrada: “If a child can't learn the way we teach, maybe we should teach the way they learn.” This dissertation mainly focuses on braille readers aged 12 and 18 years. In the Netherlands, about 50% of these students — that's about forty students — go to regular schools. The mathematical books are converted into braille and the accompanying drawings are transformed into tactile drawings.
Annemiek's research shows that it is important that we as a society, commit ourselves to inclusive education. That's education where knowledge is accessible to all students. The fact that someone has a visual impairment does not mean that he/she has no aptitude for mathematics. From Annemiek’s research, it also turns out that it is very challenging to teach mathematics to braille readers. Mathematics teachers should therefore have plenty of opportunities to delve into this matter. They should be given the opportunity to develop the didactic skills needed to teach braille readers. And of course, new and better tools also help improve mathematical education for braille readers.
The more personal aspect
Two questions for Annemiek: Annemiek, what do you think when you look back at the past four years?
“I start my dissertation with the aforementioned quote from Ignacio Estrada. That's the essence of what, in my opinion, education is about. During my research, I often realized how complicated it is to teach mathematics to braille readers. There is still much work to be done in that regard. Braille readers shouldn’t be performing poorly in mathematics because we don’t know (yet) how to teach them properly.”
What are your plans for the future?
“I want to continue to support braille readers (and their teachers) in mathematics. I also hope that I can continue to do research. I already have specific plans for a research project on mathematical equations and (tactile and audible) graphs. How can we help braille readers process mathematical equations? Furthermore, I want to commit myself more to mathematics education in developing countries. This concerns mathematics education for all students.”
Summary
In her PhD research, Annemiek investigated how braille readers can become more proficient in reading and understanding mathematical expressions. She investigated how braille readers read and understand mathematical expressions in braille, as well as how they can improve their tactile reading strategies. To achieve this goal, Annemiek developed an intervention that teaches braille readers to use tactile reading strategies with attention to the mathematical structure of expressions and equations. She also developed a course for mathematics teachers of braille readers.
"I am very grateful I was given the opportunity to do this research. The steps leading up to it were exciting and challenging. All in all it was a fantastic experience!"
We wish Annemiek all the best with her fantastic commitment to a more inclusive education!
It is quite difficult to extract information from your body. Your body is so vast that millions upon millions of messages get sent and deleted every second. It is impossible to know exactly who said something. The doctor’s main challenge is finding a way to reconstruct the network of interacting cells given the limited information she can measure.
In this article Maya continues her journey from Rotterdam to Brussels. She starts thinking about a puzzle from her childhood, the three utilities problem. At the end of the jouney she has reached a very important theorem from graph theory!
During the last decades, many resources have been invested in quantum computing. This research field has grown immensely and amazing results have been obtained. The plans for the future are highly ambitious, but at the same time, there are serious questions that need to be addressed.
Alfred Aho and Jeffrey Ullman received the 2020 A.M Turing Award for their contributions to computer science. Let’s explore how their contributions have shaped the principles, techniques and tools for writing compilers.
and 
braille characters.
). Braille is, therefore, a linear notation.
for a square root or 
for infinity. In braille, such symbols must be displayed in dots. That is difficult because the number of dots in a braille cell is limited.
(2)
(3)
