What have Donald Trump, an epidemiologist and a rock in common?

In this article, dear reader, I am going to show you in which way the development of your opinion during the last political issue, the spread of a virus among your acquaintances during the current pandemic, and the alignment of some particles lying inside the device from which you are reading this article are extremely comparable phenomena.
The travelling salesman problem
Suppose you have a delivery service. You have one truck and have to deliver a large number of parcels to different cities in the country every day. Then you run into the following problem: in which order should you visit the cities?
How do you decide who is the most important?

Imagine you’re in a remote village and only have a limited number of vaccines to distribute to protect the community from a deadly virus, who do you vaccinate?
A difficult decision, but necessary. Assuming that the disease is just as deadly for everyone in the community, the best way to prevent deaths is to contain the spread of the virus.
How many colors do you need to color a map?

A mathematician once told me that problems that are very simple to state can be very deceiving, and sometimes turn out to be extremely difficult to solve. One such problem was the Four Color Problem.
Netsweeper: playing Minesweeper without the old-fashioned grid
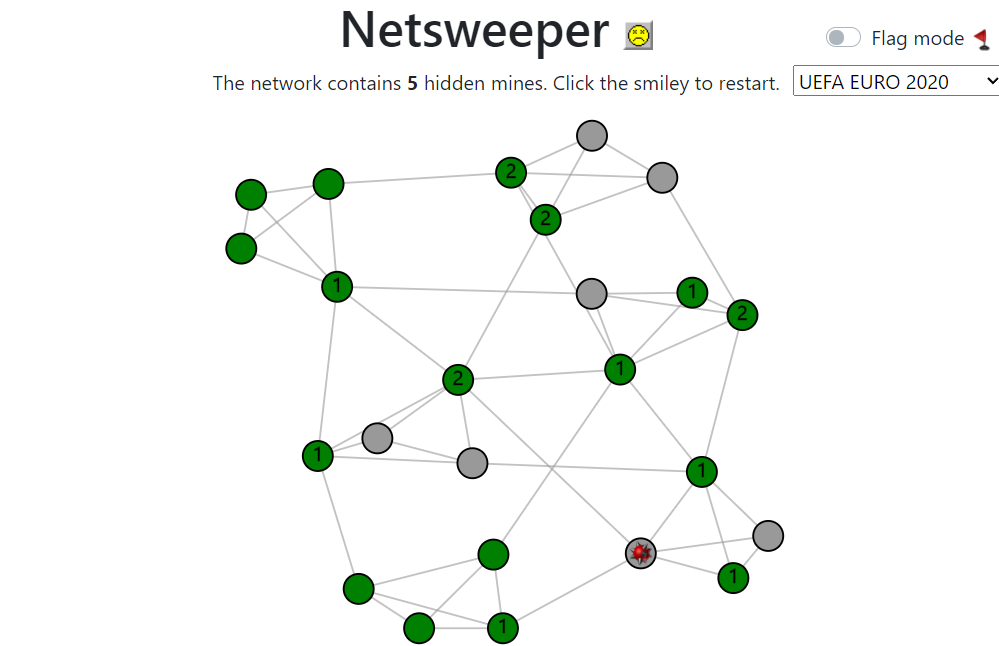
If you were born in the previous century, then chances are high that you have spent quite some hours playing Minesweeper, the classic puzzle game that used to be installed on every computer. In this article, we will present a new network-based version of this game and show how network science can help you play this game.
Percolation theory: about math and gossip

Percolation theory is a branch of mathematics at the interface between probability theory and graph theory. The term 'percolation' originates from materials science. A representative question is as follows. Suppose some liquid is poured over a porous material. Will the liquid be able to make its way from hole to hole and reach the bottom?
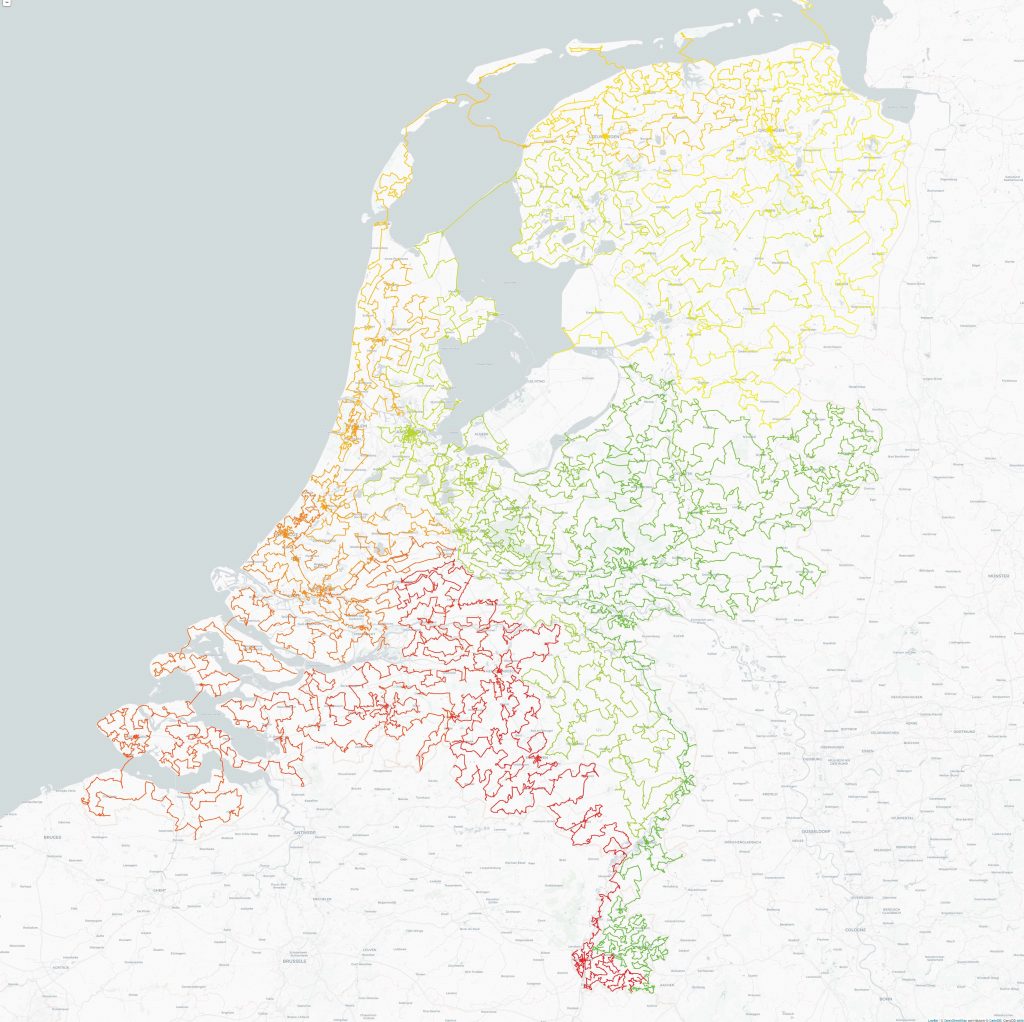
Cycling to 57,912 National Monuments in the Netherlands
In March 2021 the largest roadmap instance of the traveling salesman problem ever was solved. This is a new record for the Travelling Salesman!
A big breakthrough in the Euclidean Travelling Salesman Problem
Recently there has been a breakthrough in the field of algorithms for geometric network problems, concerning the complexity of the Euclidean Travelling Salesman Problem.
A solution to a long standing conjecture
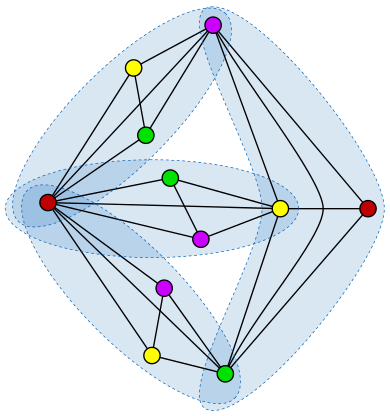
Recently a team of mathematicians has published an article announcing a solution to a long standing open problem in graph theory, the Erdős - Faber - Lovász (EFL) conjecture. This conjecture was formulated in 1972 by mathematicians Paul Erdős, Vance Faber and László Lovász.
Stumbling around in a changing world
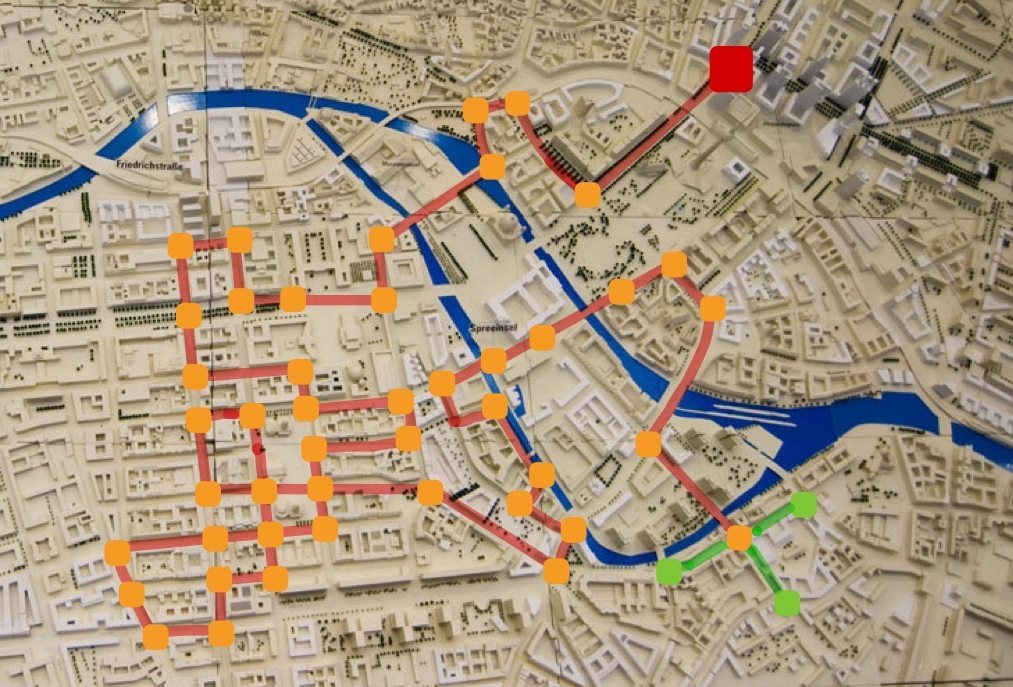
Random walks are popularly described as a drunkard’s path down the streets. What happens when the streets also start to move?
