Recently there has been a breakthrough in the field of algorithms for geometric network problems, concerning the complexity of the Euclidean Travelling Salesman Problem.
In 2019 Sándor Kisfaludi-Bak was awarded the cum laude distinction for his groundbreaking research in the field of algorithms for geometric network problems. Sándor was also awarded with the Distinguished Dissertation Award from the European Association for Theoretical Computer Science for his research. During his PhD in the group of Prof. Mark de Berg at the Eindhoven University of Technology, Sándor and his co-authors managed to solve a long-standing open problem in theoretical computer science concerning the complexity of the Euclidean Travelling Salesman Problem (ETSP). In this article we will discuss the Travelling Salesman Problem and the Euclidean version of it, and present some ideas from Sándor’s research.
A travelling salesman
Suppose you are running a delivery service. You have a single truck and each day you must deliver a large number of parcels at various cities throughout the country. Then you face the following problem: in which order should you visit the cities? In other words, you want to find a round-trip that starts at the depot where the parcels are kept, then visits each of the given cities, and finally returns to the depot. Such a round-trip is called a tour of the given cities. Of course, the goal is to find a tour with minimum travel cost. Here travel cost can refer to the average time it takes to follow the tour, or the total length of the tour. Computer scientists call this problem the Travelling Salesman Problem, or TSP for short. You may think that if we know the cities to be visited and the travel costs of the roads connecting them, then a computer can easily compute a shortest tour. But the fact that TSP is so simple to state is deceptive: it turns out finding the best tour is extremely difficult, even with state-of-the-art computers. The Travelling Salesman Problem has grown so popular that it even has its own website, with applications varying from finding the optimal pub crawl in the UK to determining the optimal interstellar tour between stars! Recently the optimal tour between 57,912 national monuments in the Netherlands has been computed!
In case the travel cost represents the distance of each road then you want a tour minimizing the total distance to travel, in case it represents travel time you want the quickest possible tour. These two tours are in general not the same, since roads guaranteeing a short distance may be more expensive, because of tolls for example, or may lead to a higher travel time, because of congestion. Can you imagine that this is one of the most challenging problems in theoretical computer science? Let’s see why this is so.
To start with, for a small amount of cities, say maximum ten, and a not so complicated road network you can think of solving this problem with pen and paper. If you start increasing the number of cities you will quickly start doubting your patience, and might write a computer program to solve it for you. What would you do if I told you that this problem, for a large number of cities, is intrinsically so difficult even for the best computer that exists? Before I proceed, you might start doubting this statement because you use navigation software every day, think of Google Maps, which produces the shortest route to a destination in less than a second. It may seem weird, but finding a shortest route between two given cities is a much simpler problem than finding a shortest tour that visits all cities in the network. To understand better how mathematicians try to solve TSP it is essential to firstly present the mathematical formulation of TSP, which is also rather simple.
From road networks to graphs
The suitable language to use in order to study problems like TSP is graph theory. Intuitively, we said that the Travelling Salesman Problem concerns finding the optimal tour visiting all cities in a road network. To translate TSP into mathematics, mathematicians use graphs. A graph is just a collection of nodes, and edges connecting some of the nodes. Each edge has a weight, which is a value associated with it, that can be interpreted as the expected travel time (or the length) of the corresponding road represented by this edge. TSP can then be stated, as a general mathematical problem, as follows:
“Given a graph consisting of n nodes, edges connecting some nodes and their corresponding weights, find an optimal route starting from a given node, visiting all nodes in the graph exactly once, and finally returning to the starting node. Or simply stated, find an optimal tour. Optimality here means that the sum of all the weights of the edges in the tour should be as small as possible.”
Thus, we see that mathematicians are interested in solving a very general problem, for any possible graph, and any possible choice of positive weights, the goal is to have an algorithm that can find the optimal tour in a reasonable amount of time. And this problem is very complicated!
Connecting the states in the US
The Travelling Salesman Problem has a rich history. The first mathematical studies related to the Travelling Salesman Problem appeared in the 1800s by the Irish mathematician Sir William Rowan Hamilton and by the British mathematician Thomas Penyngton Kirkman. The general form of the TSP appears to have been first studied by mathematicians starting in the 1930s by Karl Menger in Vienna and Harvard. A breakthrough in solution methods for TSP came in 1954, when George Dantzig, Ray Fulkerson, and Selmer Johnson used a very strong algorithmic technique called the simplex method to solve an instance of this problem with 49 cities, an impressive size at that time. With their solution Dantzig, Fulkerson and Johnson managed to find the optimal route in the road network connecting the capitals of the 49 states (in 1954) of the United States. Although a major breakthrough, their solution could be implemented only on this specific road network, this is because they relied on specific properties of the US road network to simplify the problem. A solution to the general problem, which would give an optimal route for any given weighted network, still remained out of reach.
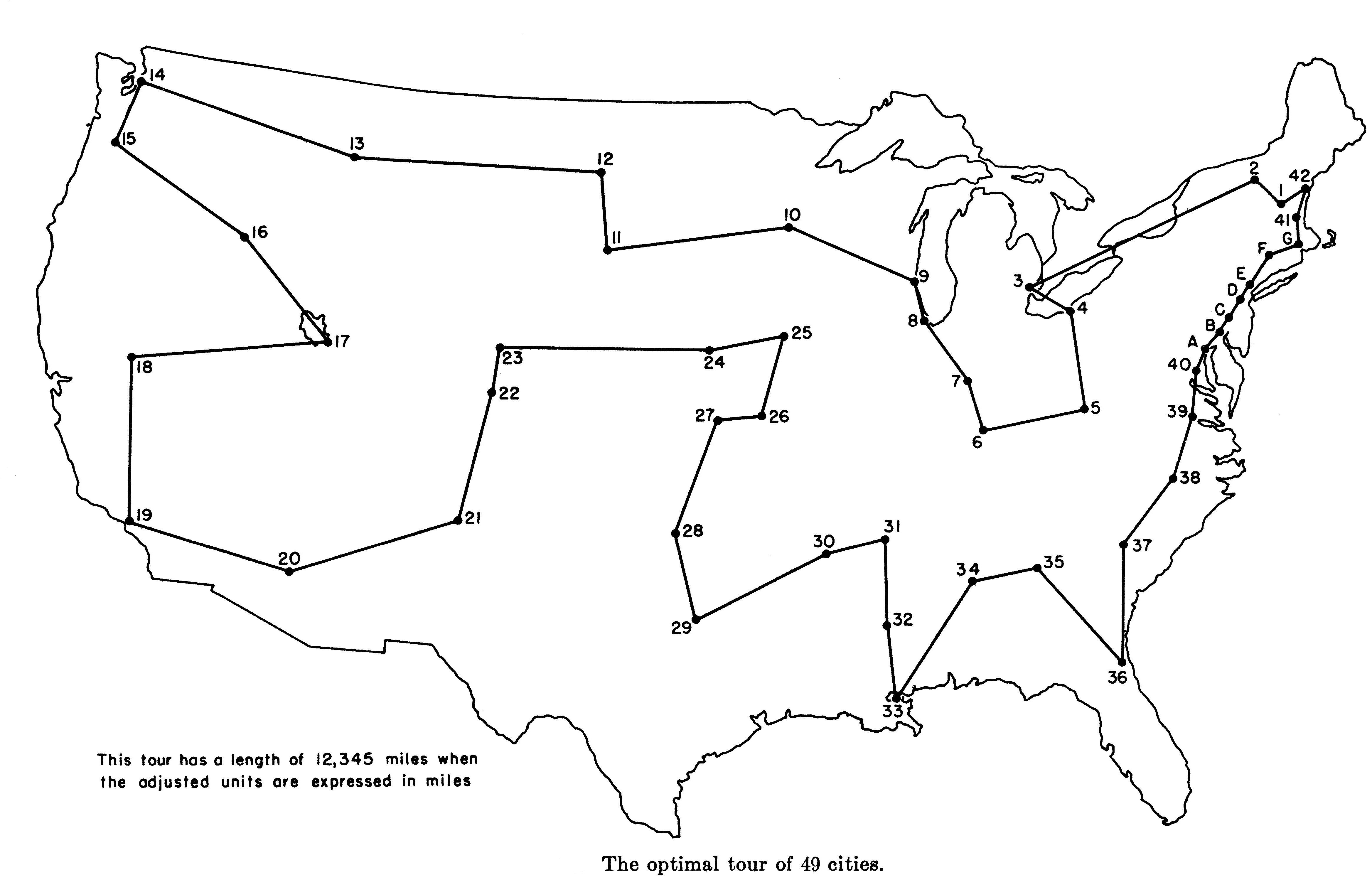
The second major breakthrough in this direction came in the sixties, independently by Michael Held and Richard M. Karp in 1961, and by Richard Bellman in 1962, who relied on a technique called dynamic programming to provide an algorithm solving the general Travelling Salesman Problem. Despite extensive efforts and progress on special cases, it is still an open problem if a better exact algorithm for TSP exists than the algorithm proposed in the sixties by Bellman, Held and Karp. You may wonder, since they managed to find an algorithm that solves the general problem, why is it still a hot research topic in theoretical computer science? Well, the answer lies in the complexity of the algorithm they invented. Their algorithm is simply too complicated when the graph gets large.
In 1972 Karp showed that the general version of TSP is what mathematicians and computer scientists call an NP-hard problem. Without going into the details, problems that are NP-hard are considered to be very difficult to solve; the time they require to give an answer grows exponentially fast as the size of the graph grows. Complexity can be thought of in the following way, given an input, how many basic steps does a computer have to make in order to give a solution to the problem.
For the Travelling Salesman Problem the Bellman-Held-Karp algorithm has complexity of the order 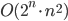 (think of the
(think of the 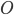 as “roughly”). This means that for a graph consisting of n nodes, a computer has to perform roughly
as “roughly”). This means that for a graph consisting of n nodes, a computer has to perform roughly 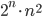 steps to come to an answer. How large do you think
steps to come to an answer. How large do you think  gets in everyday-life navigation problems? For example delivering the mail or delivering packages to customers. I would say that 100 cities is easily reached. Well, for a graph consisting of 100 cities, with all the travel times and costs from travelling from one city to the next one as weights of the graph, it takes for the computer roughly
gets in everyday-life navigation problems? For example delivering the mail or delivering packages to customers. I would say that 100 cities is easily reached. Well, for a graph consisting of 100 cities, with all the travel times and costs from travelling from one city to the next one as weights of the graph, it takes for the computer roughly 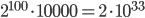 (a number with 33 digits) steps to give an answer using this algorithm. Consider you have a 2GHz processor, then this performs
(a number with 33 digits) steps to give an answer using this algorithm. Consider you have a 2GHz processor, then this performs 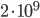 operations per second. This means that such a processor needs
operations per second. This means that such a processor needs 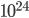 seconds to give an answer to this problem, which is an astronomical amount of time if you realize that a century has
seconds to give an answer to this problem, which is an astronomical amount of time if you realize that a century has 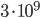 seconds.
seconds.
Of course technology companies use algorithms that can solve specific instances of TSP very fast, but what they do is similar to what the three researchers did in the 50’s with the road network of the US. They don’t solve the general problem but they use the structure of a specific case to solve it fast. In practice these algorithms give solutions that are optimal or almost optimal, but that is not guaranteed to be the case. It remains very challenging to solve TSP instances on road networks with guaranteed optimality. As far as the general problem is concerned, there exists no algorithm that can solve TSP faster than the Bellman-Held-Karp algorithm.
Geometry comes into play
To go back to Sándor’s work, in his research Sándor worked on a variant of the Travelling Salesman Problem, the Euclidean Travelling Salesman Problem, ETSP for short. In this variant more structure is imposed on the weights you are allowed to assign to the edges in the graph. In the general case these could be arbitrary positive numbers representing anything, from travel-time to distances or costs.
In the ETSP nodes are points in the Euclidean space, think just of the three-dimensional space we live in if you are not familiar with this term. This means that the weights represent distances, Euclidean distances to be mathematically precise, between the corresponding nodes. Euclidean distances are measured in a straight line, i.e., they are the distances for a helicopter pilot. Hence additional restrictions are imposed on the weights, for example they have to satisfy the triangle inequality. If from point 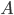 to point
to point 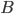 the distance is
the distance is 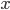 , from point
, from point 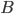 to point
to point 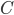 it is
it is 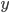 , and the distance from point
, and the distance from point 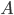 to
to 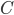 is
is 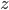 , then it has to hold that
, then it has to hold that 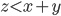 . Considering the problem in this geometric setting means that in a given tour a direct line between two nodes, say
. Considering the problem in this geometric setting means that in a given tour a direct line between two nodes, say 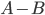 , cannot be replaced by a circuit
, cannot be replaced by a circuit 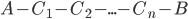 and yielding a tour of a shorter total distance. Such a restriction does not necessarily hold for travel times for example.
and yielding a tour of a shorter total distance. Such a restriction does not necessarily hold for travel times for example.
ETSP is still NP-hard, which was already shown in the 1970s, so it cannot be solved in polynomial time. Nevertheless, it can be solved much faster than the general TSP. While the complexity of the general TSP reaches the inaccessible number of 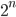 , it was shown in the 1990s that ETSP can be solved in
, it was shown in the 1990s that ETSP can be solved in 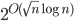 , which is significantly faster. This is where things stood for over 20 years, until Sándor and his colleagues showed that it can be solved even faster. Their algorithm runs in
, which is significantly faster. This is where things stood for over 20 years, until Sándor and his colleagues showed that it can be solved even faster. Their algorithm runs in 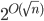 steps. For
steps. For 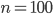 ,
, 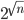 is equal to
is equal to 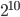 which is just 1024. This is a number of steps a computer can perform in less than a second. Moreover they also showed that a significantly better algorithm is highly unlikely to exist!
which is just 1024. This is a number of steps a computer can perform in less than a second. Moreover they also showed that a significantly better algorithm is highly unlikely to exist!
Separating and conquering
Sandor’s improvement is based on two clever mathematical techniques: separators and divide-and-conquer algorithms.
Roughly speaking, the separator technique works as follows. Suppose the points to be visited by the tour can be partitioned into two clusters of points, A and B, that are relatively far from each other. Suppose cluster A contains the starting point of the tour. Then an optimal solution would first visit some points in cluster A, then go to cluster B to visit all points there, and then return to cluster A to visit the remaining points and return to the starting location. This knowledge can be exploited by an algorithm that finds an optimal tour. Unfortunately, an ETSP instance typically does not consist of two nicely separated clusters. A main ingredient of this work is an ingenious method to separate any possible set of points into two "clusters" such that an optimal tour will not go back and forth between the clusters many times.
Divide-and-conquer algorithms are a very delicate but also a very strong tool in algorithmics. These algorithms rely on the idea that a difficult problem can be divided into smaller problems and solutions to these smaller problems can help to construct a solution to the original problem. Using the separator technique discussed above and a divide-and-conquer algorithm, Sándor and his co-authors succeeded in finding an algorithm to solve ETSP as fast as possible. The innovation in this work is in the new separator and in the application of a recent algorithmic trick in the divide and conquer technique.
 At the time we were working on separator theorems for geometric objects, and I was wondering if we could adapt our separators to ETSP and get a running time of
At the time we were working on separator theorems for geometric objects, and I was wondering if we could adapt our separators to ETSP and get a running time of 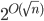 . We started looking at it more closely with Mark (Mark de Berg) and we were getting very enthusiastic. We quickly saw the type of separator we would need. It then took some time to come up with a precise formulation and a proof; in the case of the separator theorem the proof came largely from Mark. We also involved Hans (Hans Bodlaender, professor at Utrecht University and at the Eindhoven University of Technology) and Sudeshna (Sudeshna Kolay, Assistant Professor at the Department of Computer Science and Engineering at IIT Kharagpur), and they helped with some other aspects of the algorithm.
. We started looking at it more closely with Mark (Mark de Berg) and we were getting very enthusiastic. We quickly saw the type of separator we would need. It then took some time to come up with a precise formulation and a proof; in the case of the separator theorem the proof came largely from Mark. We also involved Hans (Hans Bodlaender, professor at Utrecht University and at the Eindhoven University of Technology) and Sudeshna (Sudeshna Kolay, Assistant Professor at the Department of Computer Science and Engineering at IIT Kharagpur), and they helped with some other aspects of the algorithm.
Regarding the future of the problem, I am on very shaky ground, but I will speculate a bit. On one hand, there is no more incremental progress possible, unless a big breakthrough happens. We could of course start working on nailing the asymptotics: the current upper and lower bound are still quite far from each other as the asymptotic notation is in the exponent. A different line of research regarding ETSP is to look at approximation algorithms and optimize the running times of those. In a recent paper we pretty much did exactly this.
Sándor
Conclusion
The Travelling Salesman Problem is a problem with a longstanding history and although it is very simple to state, solving it in full generality is very challenging. By considering the problem in Euclidean space, which means that the weights of the edges represent Euclidean distances, the complexity can be reduced. Sándor and his co-authors managed to construct an algorithm that solves ETSP in roughly 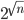 steps but they also showed that a better performing algorithm is unlikely to exist, a groundbreaking result on one of the most famous problems in computer science
steps but they also showed that a better performing algorithm is unlikely to exist, a groundbreaking result on one of the most famous problems in computer science
Sándor is currently a PostDoc at the Institute for Theoretical Studies at ETH Zürich and will move soon to Aalto University in Finland starting as an assistant professor. We wish him the best with his research trying to make complex problems more tangible.