Recently a team of mathematicians has published an article announcing a solution to a long standing open problem in graph theory, the Erdős - Faber - Lovász (EFL) conjecture. This conjecture was formulated in 1972 by mathematicians Paul Erdős, Vance Faber and László Lovász.
In Januari 2021 mathematicians Dongyeap Kang, Tom Kelly, Daniela Kuhn, Abhishek Methuku, and Deryk Osthus announced a proof of the conjecture (which holds for graphs that are large enough to be precise). If their proof turns out to be correct then the EFL conjecture will officially be promoted to a theorem! At least for all graphs that are large enough.
Let's see what the conjecture is about.
Colorings of graphs
The EFL conjecture concerns colorings of graphs. A lot of problems in discrete mathematics and in graph theory concern colorings, a famous example being the four-coloring theorem. The general question is to find the least amount of colors needed (called the coloring number) to color all vertices in a given graph such that no neighboring vertices have the same color. We also call such a coloring a proper coloring.
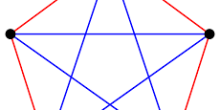
To see an example, can you find the coloring number of the following graph? You can start by giving a color to some vertex, say blue.
The four points that are directly connected to the blue point cannot be painted blue. We also see that the two points left and right of the blue point are connected to each other, hence these two points need to have different colors.
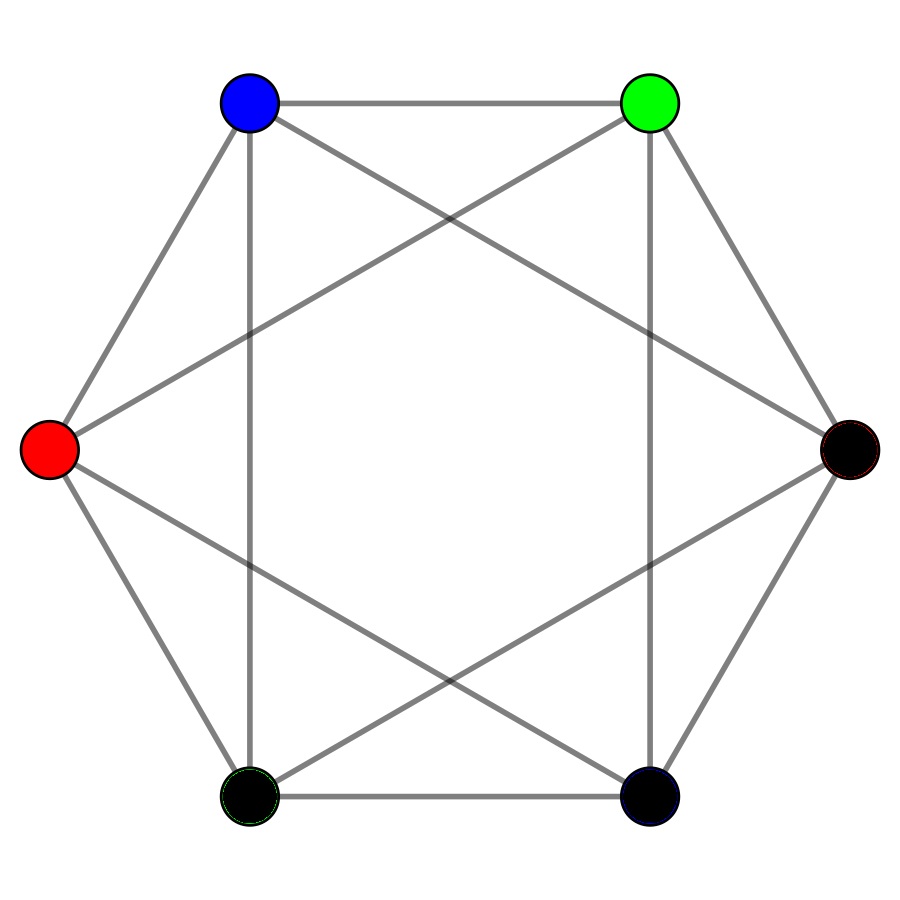
Because the graph is symmetric we observe that we would obtain a similar colored triangle no matter from which vertex we would start. Now it remains to see how we should color the remaining three points. We leave it to the reader to finish the coloring, in the end the fun in mathematics lies in doing it on your own!
The EFL conjecture
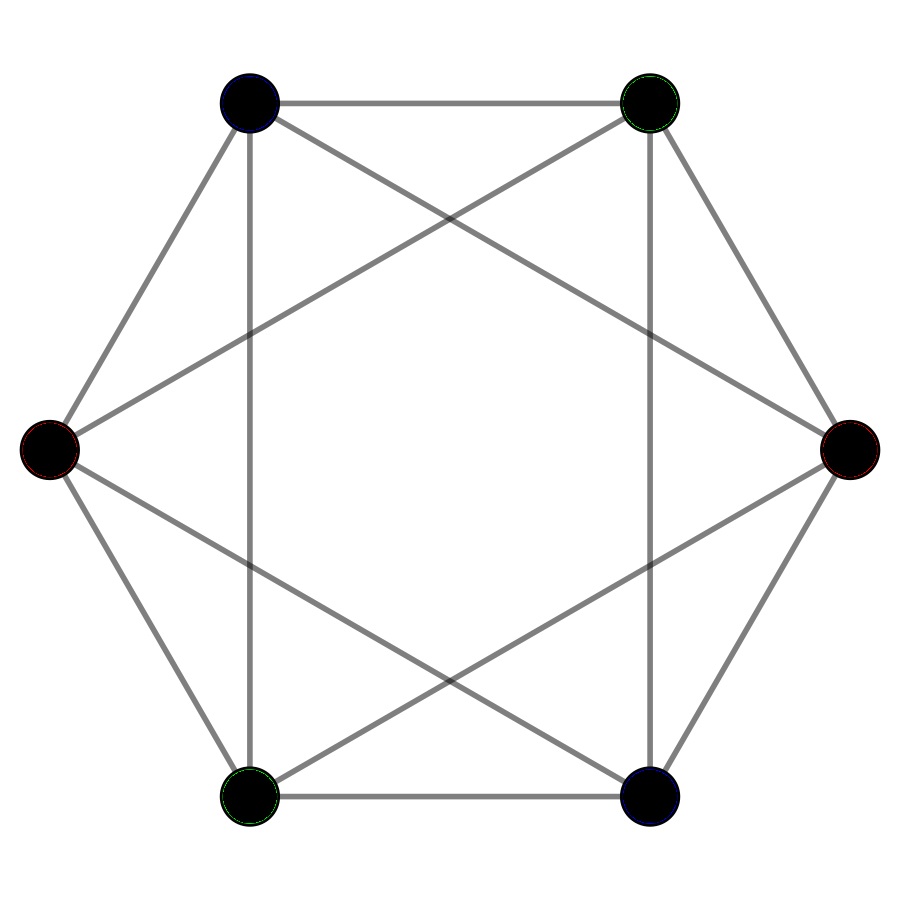
The EFL conjecture concerns colorings of graphs. To state it we need the concept of a complete graph. A complete graph is a graph where all possible pairs of vertices are connected to each other with an edge. Below you can see the complete graph on six vertices.
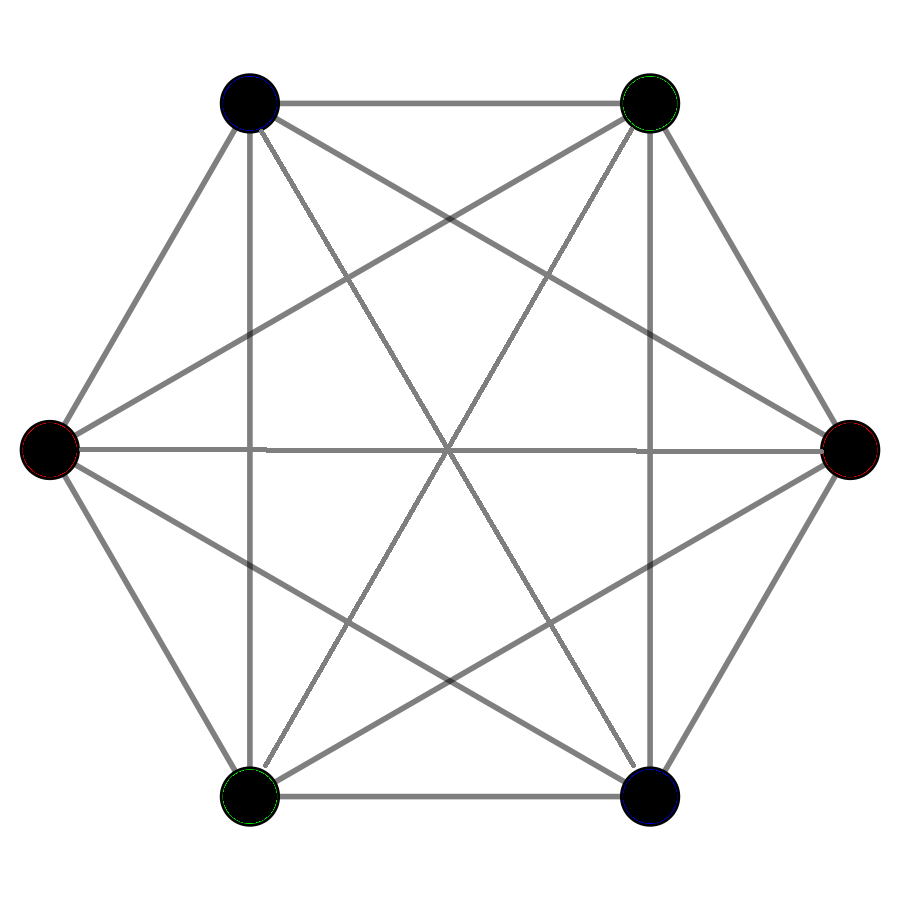
How many colors do you need to color a complete graph with  vertices? If you try to color the example above you will see that in a complete graph all vertices must have a different color (why?).
vertices? If you try to color the example above you will see that in a complete graph all vertices must have a different color (why?).
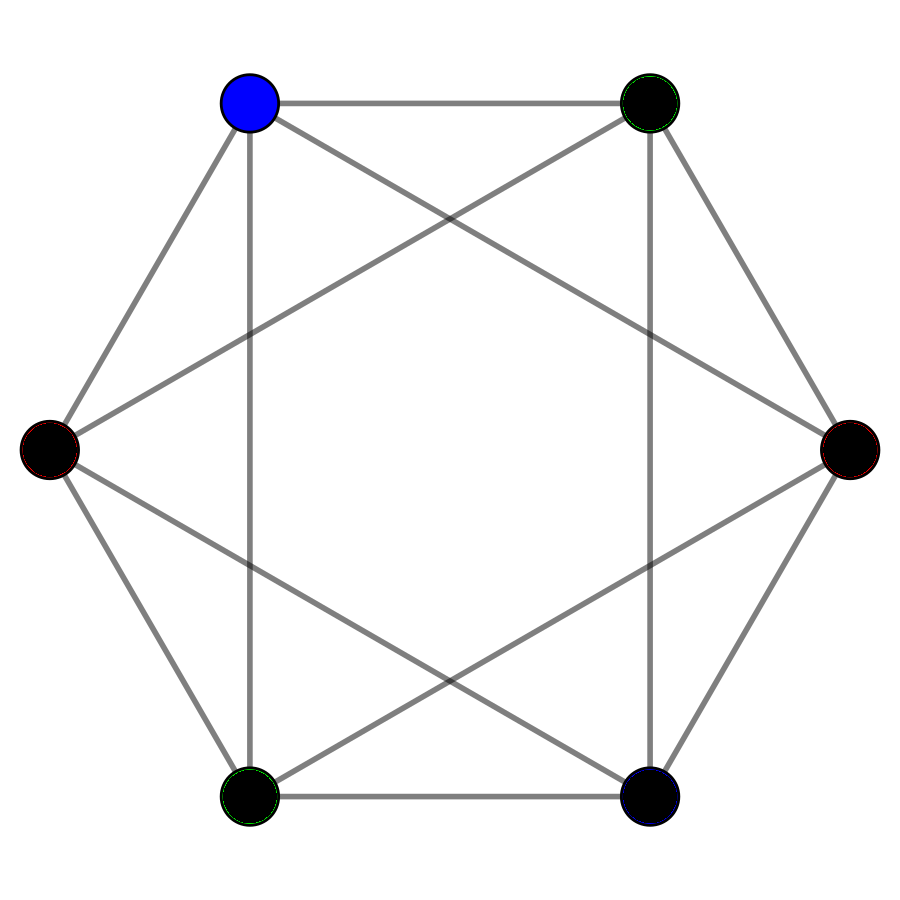
The EFL congecture concerns complete graphs that share vertices. Two graphs share vertices if they have vertices in common. Below an example of two complete graphs with six vertices sharing one vertex.
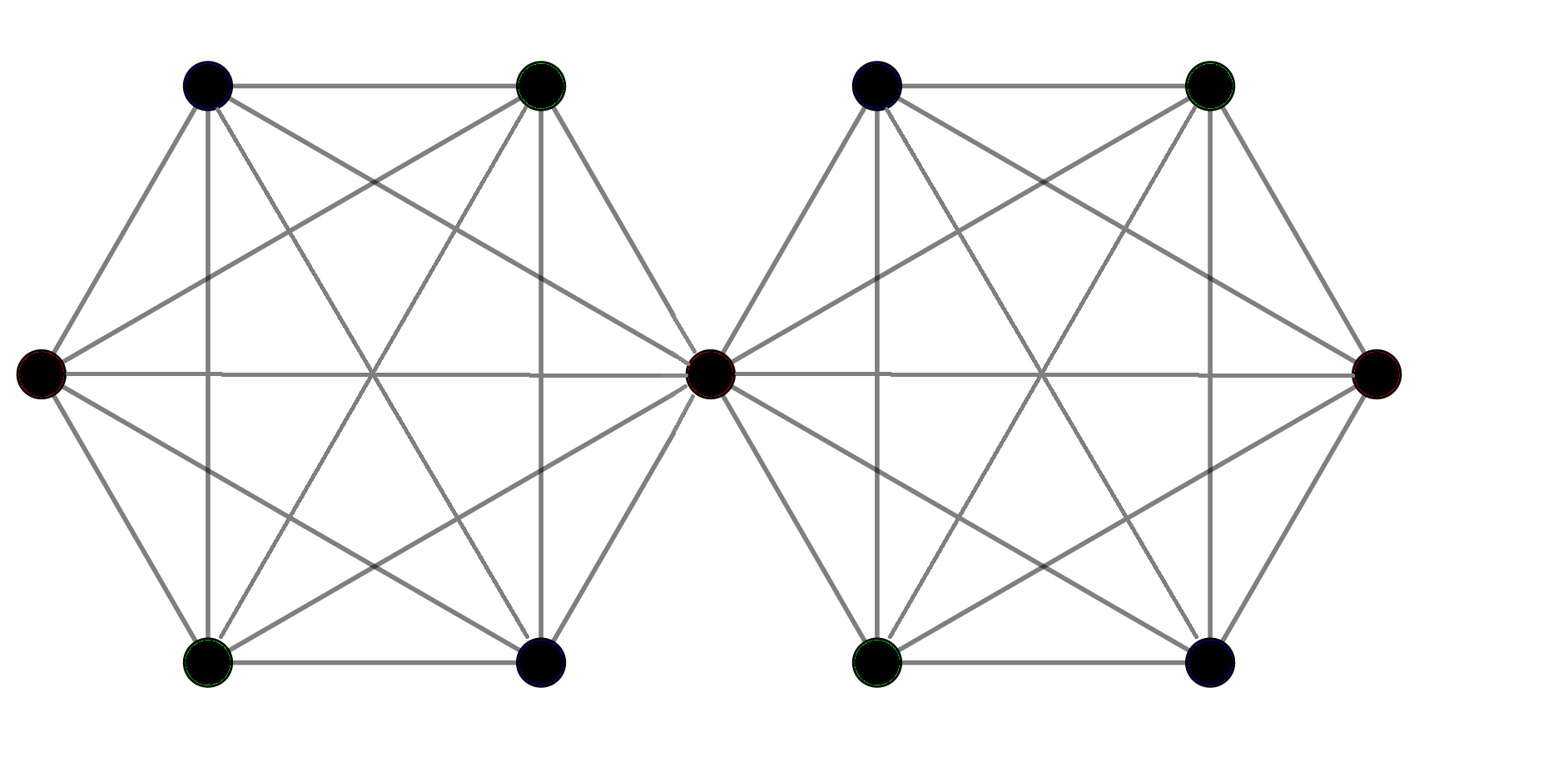
This specific combination of the two complete graphs can be colored using the same amount of colors as for the single complete graph.
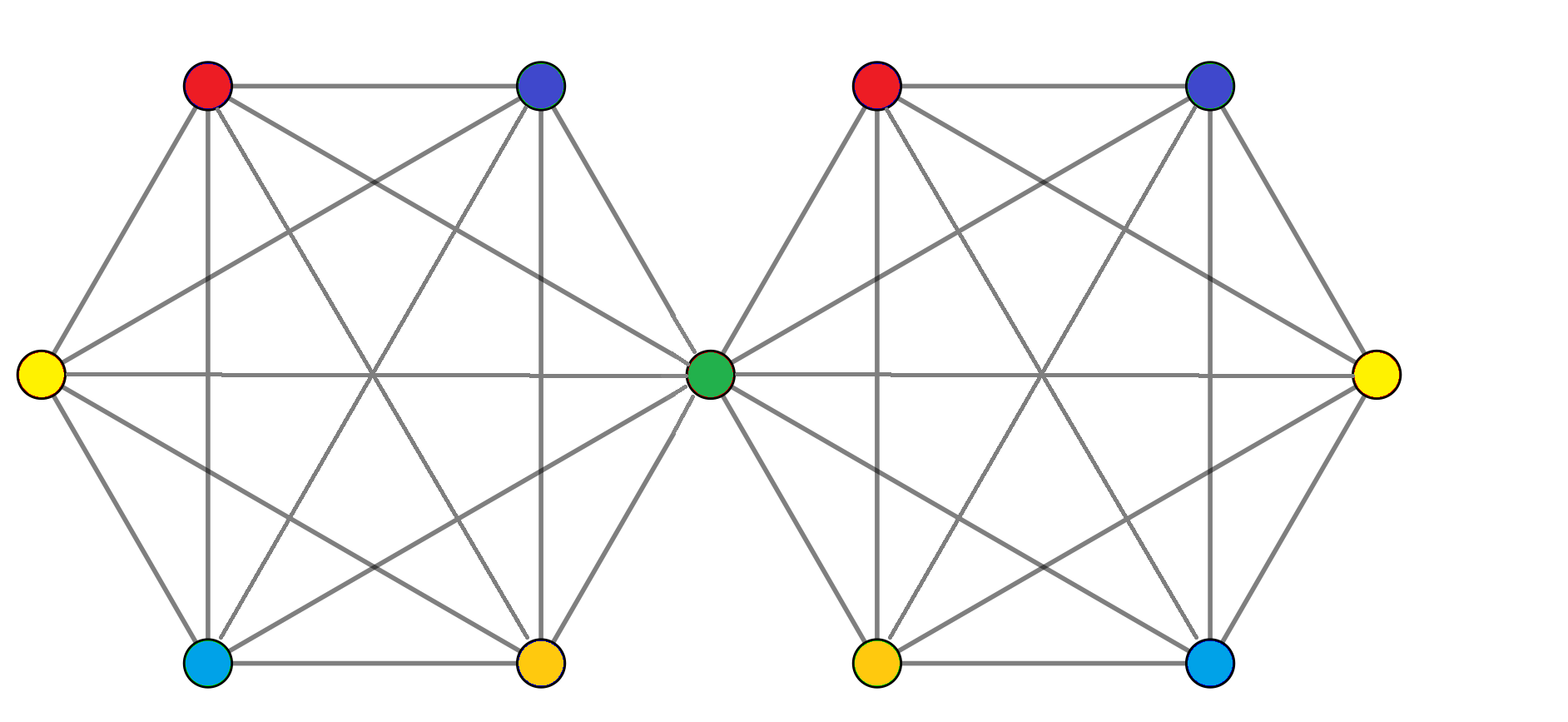
Feel free to experiment with other examples as well, also with more than one sharing vertices, and try to find the coloring numbers of the graphs that you get. This idea of complete graphs that share vertices lies at the heart of the EFL conjecture. Below the exact formulation of the conjecture.
The EFL conjecture
If  complete graphs, each having exactly
complete graphs, each having exactly  vertices, have the property that every pair of complete graphs has at most one shared vertex, then the union of the graphs can be properly colored with
vertices, have the property that every pair of complete graphs has at most one shared vertex, then the union of the graphs can be properly colored with  colors.
colors.
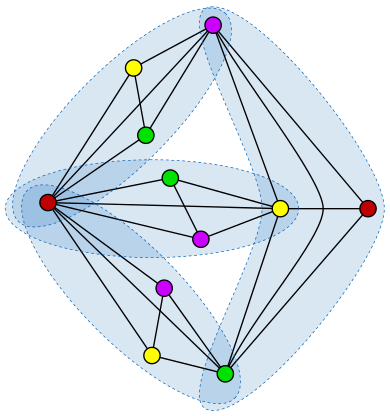
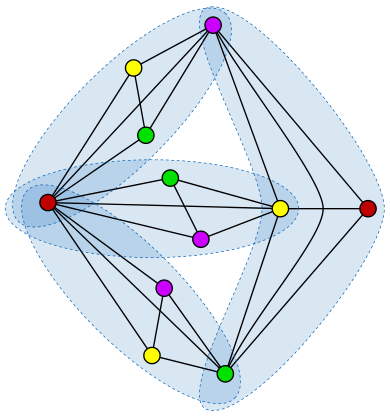
In he figure below (taken from Wikipedia) you can see the solution for the case of 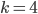 , that is the case you have four complete graphs ofsize
, that is the case you have four complete graphs ofsize 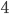 such that every two of the graphs have exactly one vertex in common.
such that every two of the graphs have exactly one vertex in common.
To conclude, in a talk, mathematician and contributor to the published article, Tom Kelly described the depth of this problem using a quote from Paul Erdős:
"Problems have always been essential part of my mathematical life. A well chosen problem can isolate an essential difficulty in a particular area, serving as a benchmark against which progress in this area can be measured. An innocent looking problem often gives no hint as to its true nature. It might be like a “marshmallow,” serving as a tasty tidbit supplying a few moments of fleeting enjoyment. Or it might be like an “acorn,” requiring deep and subtle new insights from which a mighty oak can develop."
The EFL-conjecture is definitely an acorn!