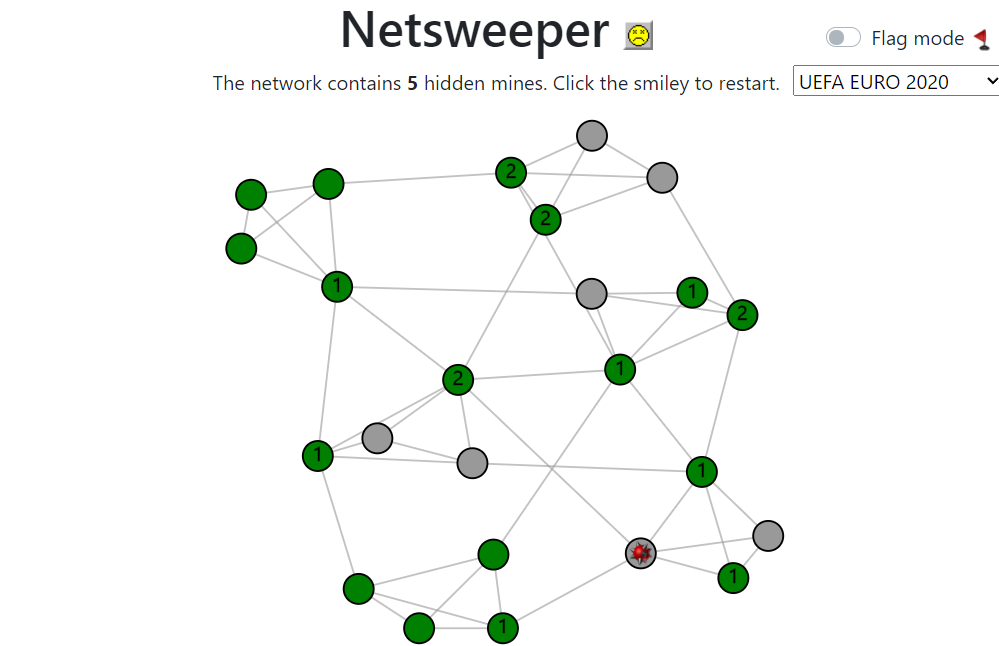
How network science can help you play this fun new variant of the classic computer game.
If you were born in the previous century, then chances are high that you have spent quite some hours playing Minesweeper, the classic puzzle game that used to be installed on every computer. In this article, we will present a new network-based version of this game and show how network science can help you play this game.
Minesweeper
The original game is played on a grid where each square may or may not contain a mine. The goal is to step on all squares that do not contain a mine, while not stepping on any mines. You can step on a square by clicking on it. If the clicked square contains a mine, then the game ends and you lose (your foot). Interestingly, in the initial version, the cursor was a foot that would explode and turn into a bloody stump when stepping on a mine. This cursor was removed in later versions for obvious reasons. If the square does not contain a mine, then it will show the number of mines that are on the 8 adjacent squares. If there are no mines on adjacent squares, then these adjacent squares will also automatically be ‘stepped on’.
The game is won when all squares without mines have been stepped on. If this description does not yet trigger nostalgia, then it may be good to try out the original game before reading the rest of the article.
There exist many variants of this game, including versions with triangular grids, hexagonal grids and three-dimensional layouts. If we look at this game and these variants more abstractly, then what all these versions have in common is that the ‘minefield’ can be described as a number of locations (squares, triangles, hexagons or cubes) and some way of telling which locations are adjacent. The minefield could then be viewed as a network where each node corresponds to a location and where adjacent locations are connected by a link. This abstract way of looking at the game allows us to come up with many different versions of the game by simply replacing this network. For example, we could simply take the twelve provinces of the Netherlands as nodes and connect them by a link if they share a border. We could go even further than this by abandoning the notion that the network should represent adjacent shapes. For example, we could create a network out of the UEFA EURO 2020 football cup where each node represents one of the 24 football teams and each link represents one of the 51 matches. In such a game, would you start by stepping on the team that won the tournament (and thus played against the most other teams), or would you start with a team that dropped out at the beginning?
Introducing Netsweeper
This gives us a far more general version of the original Minesweeper game, that we name Netsweeper, since we replace the old-fashioned grid by a network. The game can be played at the bottom of this page. In the remainder of this article, we will discuss strategies for playing this game, and how this strategy depends on the characteristics of the network that we are playing on. This will help you sweep through any network, and you might also learn some network science on the way!
Basic deduction rules
We start by summarizing two basic strategies of Minesweeper that can also be followed for Netsweeper: firstly, if after stepping on a node, it indicates that it has one mine in its neighborhood, while we see that all but one neighbors have already been stepped on, then we can deduce that this last neighbor must contain a mine. Of course, this rule also works for numbers higher than one: if the number indicated on the mine is equal to the number of unknown neighbors, then we know that all these neighbors contain mines.
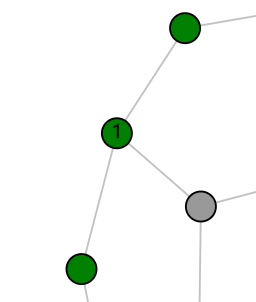
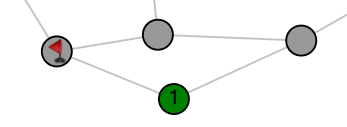
Secondly, if we have located a mine (and conveniently marked it with a flag) and see that one of its neighbors has a 1 on it, then we know that all other neighbors of that 1-node cannot contain mines, so that we can safely step on them. Again, this rule also works for higher numbers of mines.
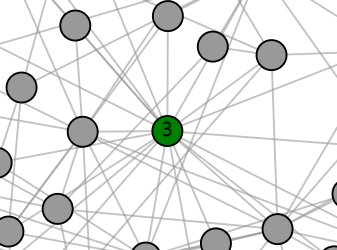
Avoiding hubs
If the network contains some nodes with many links, it may affect the way you play the game. In network science, nodes with many links are often referred to as hubs. The neighborhood of such a hub likely contains many mines, along with many non-mines. Therefore, when we step on such a node and get to know the number of mines in its neighborhood (assuming it itself is not a mine), it is unlikely that it will allow us to apply any of the deduction rules above. Therefore, especially at the beginning of the game, it can be helpful to avoid stepping on hubs and focus on the nodes with fewer neighbors.
Divide and conquer
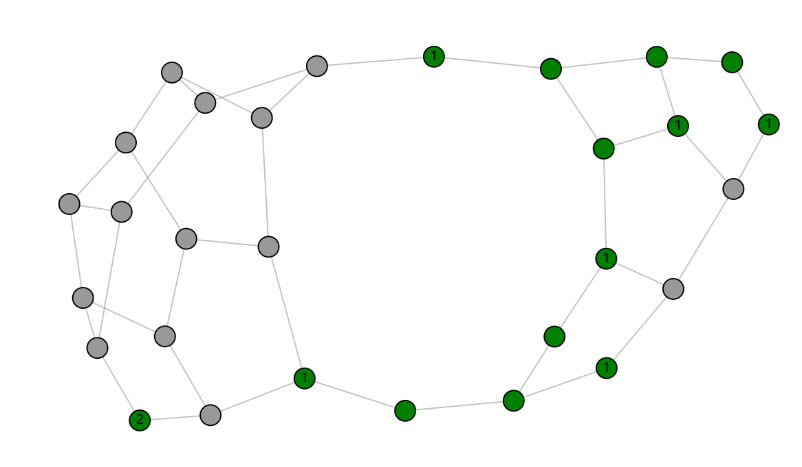
One disadvantage of playing minesweeper on a network rather than a grid is that the links may sometimes clutter the view, making it difficult to get a good overview of the network. In our game, when clicking on a node that has already been stepped on and does not neighbor any mines, the node and its links will be deleted. This is especially helpful when the network consists of loosely connected components. When disconnecting these, one can look at each of the components independently, as several smaller minefields.
Symmetry and randomness
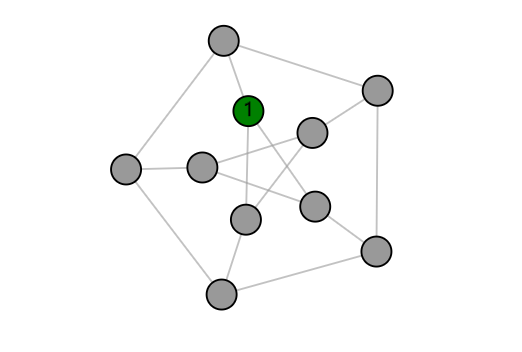
If the network that we are playing on has many symmetries, then this may influence the gameplay. Take for example the network shown on the right, which is known as the Petersen graph. You may notice that this network looks somewhat symmetric, since rotating the figure by one fifth will not change the image. Actually, this network is completely symmetric: we can move any node to the place of another node and then rearrange the other nodes so that we obtain the original image again.
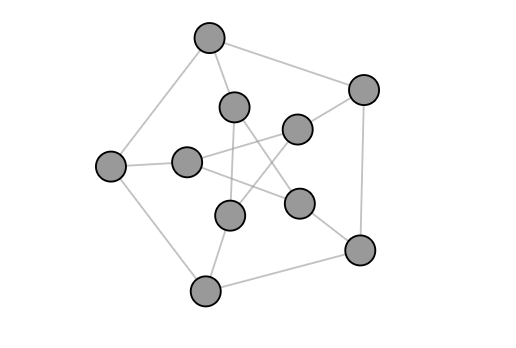
Therefore, at the beginning of the game, it doesn’t matter on which node you click, as they are all the same.
Now suppose that we know that this network contains three mines and that after stepping on the first node, we see it has one mine in its neighborhood. Then we know that one of the three neighbors must have a mine, while the six remaining nodes must contain two mines. This means that, whichever node we click, we have a 2/6=1/3 probability of stepping on a mine. Again, the symmetry results in (probabilistically) the same outcomes for every move.
Randomly generated networks
In this article, I named several networks on which Netsweeper can be played. However, there are many more possibilities, and some are already available in the game. Two of these networks are also randomly generated, so that each time you restart the game, you will step into a different minefield.
The first and simplest random network is the Erdős–Rényi network. Here we have a number of nodes, and for each pair of nodes, we randomly decide (say, by tossing a biased coin) whether to place a link between them or not.
The second random network is the preferential attachment network. A network that is generated by iteratively adding nodes to the network and connecting (attaching) them to existing nodes randomly, but with a higher probability (preference) of connecting to nodes that already have many neighbors. This results in a network that likely contains a few hubs, which makes the game more difficult. For more about preferential attachment networks, you can read this article.
The game can be played below. If you are on your computer, flags can be placed by right-clicking. When you’re on the phone, you can place flags by toggling to “Flag mode” before clicking on the node where you want to place the flag. To change the network, select one in the drop-down menu and click the smiley to restart the game.
This gives us endless minefields to sweep. Each network has its own characteristics which influence the gameplay and strategy. Do you notice this difference when playing on the different networks? And can you also see which characteristics cause these differences?
Have you ever wondered what kind of insights you can gain about games by looking at it using a mathematical lens? In this article we have a look at Snakes and Ladders, and in a follow up article we will dive into Monopoly!
One of the main building blocks of modern AI-tools are artificial neural networks, abstract models inspired by the structure and functions of biological neural networks which enable machines to "learn". In this article, I will discuss some thoughts on this topic.
A mathematician once told me that problems that are very simple to state can be very deceiving, and sometimes turn out to be extremely difficult to solve. One such problem was the Four Color Problem.
