Suppose you’re in charge of organizing the Valentine’s day activity for your high school class: a date night. All interested singles send you their (secret) list of the people they fancy and would find acceptable as a Valentine’s date. As organizer, you are the only one with access to the lists. Using this information, it is your task to make a schedule of who dates whom on February 14th.
Your task is not an easy one. To prevent heartbreak and jealousy, no-one should be assigned more than one dating partner for the evening. You should respect people’s wishes: if you plan a date between Alice and Bob, then Bob should appear on Alice’s list, and Alice on Bob’s. To ensure maximum love potential, you want to make a schedule in which the largest possible number of students gets a date: no one should be alone without good reason!
Finding a dating schedule that matches pairs of potential lovers up into dating couples, is an example of an algorithmic problem. There is a clearly defined input, given by the lists of who is considered an acceptable dating partner to whom. It is also clear what we want as the output: a pairing of classmates into acceptable boy-girl pairs that has as many pairs (dates) as possible.
How can you find the best dating schedule? A brute force approach would be the following: try all ways of pairing up the students. For each pairing, check the preference lists to see if all dates are between mutually interested students, and use the first valid schedule you find this way. While this approach works in principle, it leaves much to be desired in practice. Suppose your class has 15 boys and 15 girls. There are 15 options for a partner for the first girl; 14 options for a partner for the second girl; and so on. In total, there are 1514 … * 321 = 1307674368000 different pairings for a class of this size. Even if you worked at the speed up a modern computer, checking a million different schedule every second, it would take you a year to go through that many possibilities.
Luckily, there is a much better approach to find the best schedule, based on clever mathematical insights. To use it for a class with 15 boys and girls, you only need to consider 15 schedules throughout the process, rather than the billions of possibilities in the brute-force solution!
My goal in this article is to teach you the algorithm for finding the best dating schedule. It is a structured series of steps that is guaranteed to lead to an optimal solution. It’s a bit like an IKEA manual for assembling a piece of furniture: it gives step-by-step instructions on how to proceed. But while an IKEA manual works only to build one particular type of furniture (bookcase Billy) from one particular packet of materials, the algorithm works for any input (your classmate's preference lists), and always produces a correct output (a best-possible dating schedule).
You can follow the steps of the algorithm to find the best Valentine’s day schedule; but the algorithm has a wide range of other important applications. It is executed by computers on a day to day basis to assign people to jobs they are qualified for; to assign university freshmen to available spots at universities and dorm rooms; and to assign players of approximately equal rank to free spots in online multiplayer games. By understanding the algorithm, you will get a good sense of how the decision-making in many of these digital systems is being done. Since decisions based on algorithms and artificial intelligence are becoming the cornerstone of day to day life, this understanding will help you to trust the decisions made by the computer. If you have some programming skills, then after reading this article you will also be able to implement the algorithm in the programming language of your choice. But my explanation here will involve nothing more complicated than post-it’s, to make it accessible to all.
Outline of the algorithm
The algorithm works on a network that encodes everyone’s preferences. An example is shown below, for a class with 5 boys and 5 girls. There is a node for every student in the class. Two nodes are connected by a line, if they find each other acceptable to date.
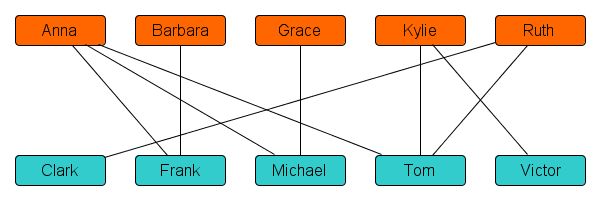
In the example above, there is no line between Anna and Clark, so Anna and Clark are not acceptable partners to each other. That happens when Anna is not on Clark’s list, or Clark is not on Anna’s list – or both. The line between Anna and Frank shows that they would be happy to date together. In this situation, we say that they are compatible dating partners.
As a first step in making a dating schedule, let’s assign partners in alphabetical order. The first boy that is an acceptable match for Anna is Frank, so let’s tentatively plan a date between Anna and Frank. (We might later come back to this decision.) After Anna, we get to Barbara. Unfortunately, her only potential partner Frank is already taken and so we cannot assign her any partner. We skip over to Grace, who is matched to her first free partner Michael. Then we match Kylie to Tom, and Ruth to Clark. This leads to the following schedule, where pairs that are matched to date are highlighted in red:
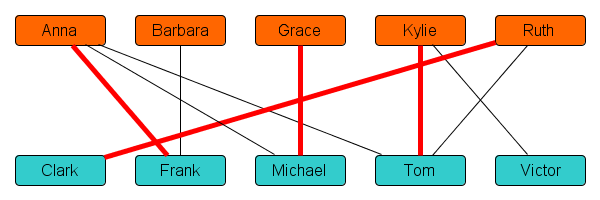
Unfortunately, in this tentative schedule two students are left out in the cold: Barbara and Victor do not get to date. They do not fancy each other, so we cannot plan a date for them as a couple. Is there anything we can do?
If you look closely, you’ll see that this schedule can be re-arranged to accommodate everyone! Recall that Barbara and Victor were the unlucky date-less people in the first draft of the schedule. Now consider the following structure in the network:
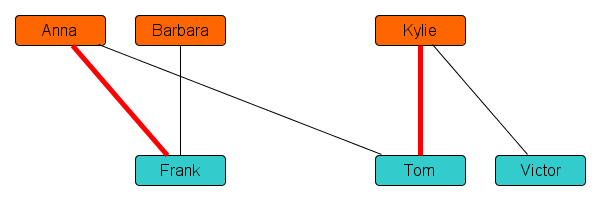
The drawn path in the network connects Barbara to Victor via an alternating sequence of lines: the first black line from Barbara to Frank is a potential match, but not scheduled; the next red line from Frank to Anna is a scheduled date; the black line from Anna to Tom is a potential match, but not scheduled, and so on.
A structure like this, connecting two unmatched people via lines that alternate between scheduled dates and potential dates, is called an augmenting path. It encodes how the schedule can be improved to provide more dates! If we re-assign Frank to Barbara, and Tom to Anna, then that leaves Kylie free as an interested partner for Victor. So effectively, the dating schedule is updated by cancelling the dates indicated by red lines on the augmenting path, and planning the dates indicated by its black lines instead. This leads to the following dating schedule, in which everyone gets a suitable partner:
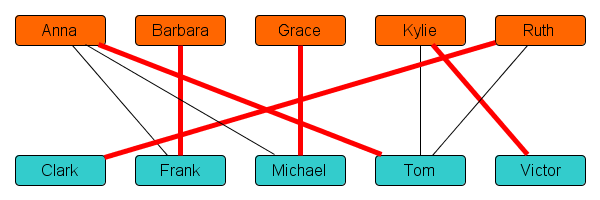
By updating the initial alphabetical dating schedule using the augmenting path structure, we obtained a good plan for Valentine’s day for this example class of 10 students. Now let’s discuss how the approach works for larger classes. The key idea in the algorithm is to repeatedly improve the schedule, until it cannot be improved any more.
To do an improvement step, we need an augmenting path as above, which connects an unmatched girl to an unmatched boy by lines that alternate between potential and scheduled dates. If we know an augmenting path in the network, we cancel all the previously planned dates on the path, and schedule the other dates on the path. Since an augmenting path starts and ends with a black line, and alternates between black and red lines, there are more black than red lines on the path. Hence by replacing the red planned dates by the black ones, the total number of planned dates increases!
The overall procedure therefore is the following:
Build a first version of the schedule: Consider the girls in alphabetical order, and assign each girl the first available compatible boy.
If the network representing the current dating schedule contains an augmenting path, connecting an unmatched girl to an unmatched boy via lines that alternate between planned dates and potential dates, then update the schedule as described above. The total number of planned dates increases by one. Repeat this improvement step as long as there is an augmenting path in the network.
If no further augmenting path can be found, use the resulting schedule as the final answer.
Let’s see why this is indeed an efficient way to solve the problem. Each time an augmenting path is found, the number of scheduled dates increases by one. In a class with N girls and N boys, the optimal schedule has at most N dates in total: by our jealousy-prevention rule, each student can be involved in at most one date. Since the number of scheduled dates increases whenever we find an augmenting path, and can never grow beyond N, the entire procedure must finish after finding at most N augmenting paths. Each augmenting path that we find leads to a new tentative dating schedule. So for a class of 15 boys and girls, we have to consider at most 15 tentative schedules before we find the final answer. That’s a huge improvement compared to the millions of schedules that the brute-force approach looks through!
The outline above describes the efficient augmenting-path algorithm to find a best-possible schedule of dates between two groups of students. More generally, it finds what’s called a maximum matching in a network of entities of two types (boys and girls; tasks and employees; prospective students and dorm-room places; and so on). It is an elegant example of a powerful algorithmic paradigm.
More advanced algorithms based on augmenting paths are used every day. In fact, a series of recently declassified documents revealed the following: during the cold war, the USA used an augmenting-path algorithm to compute the most efficient way to disrupt train transports in the Soviet Union! The computed plans describe how to disrupt all transports from Moscow to the Western front using the least amount of airstrikes. Luckily, they were never executed.
Let’s take our bearings; what did we achieve so far? You’ve seen the outline of the algorithm and understood why it is much more efficient than the brute force approach. However, there are some important details that the outline glosses over: how should you find an augmenting path? How can that be done in a structured way, and quickly? This is where the post-it’s come in; we’ll look at those details in the next section. The other important aspect that we still have not covered is: why does the approach always give a best-possible dating schedule? I will explain that afterwards. After seeing the proof, you will be able to trust the fact that the algorithm indeed gives us the best-possible answer.
Why do we always find a best-possible dating schedule?
Now that you’ve understood the overall approach using augmenting paths, and have seen how augmenting paths can be found using post-it’s, the last aspect that we consider is the following: is the schedule we find using the algorithm always best-possible? Can we be sure that a dating schedule computed in this way, never causes people to sit alone, unmatched, without good reason?
After the time investment of understanding the algorithm, you’ll be happy to learn that yes, the output you get from the algorithm is always a best-possible dating schedule: no other schedule will contain more dates, and the found schedule only matches pairs that were mutually interested. This does not necessarily mean that all students get a date in the schedule. Depending on the preference lists, it may not be possible to find a dating schedule where everyone gets a date. Consider the following example:
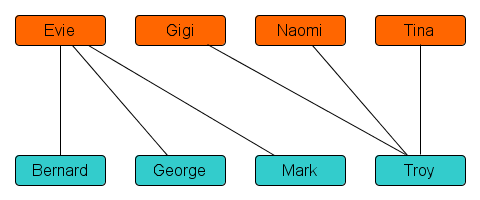
If the preference lists lead to the network above, then not everyone can get a date. Since all potential dates either involve Evie or Troy, both of which can get only a single partner by the jealousy-prevention rule, a best-possible dating schedule for this class will consist of only two dates. There are several options; for example “Evie-Bernard,Tina-Troy” is an optimal matching; but “Evie-Mark,Gigi-Troy” is an equally good matching. The quality of the schedule is determined solely by how many compatible dates are planned.
Armed with this understanding of what it means for a dating schedule to be optimal, let’s see why the augmenting-path algorithm always leads to an optimal solution. The algorithm only stops when the network, with up/down directions based on which dates are currently scheduled, does not contain an augmenting path. To prove that the algorithm finds an optimal matching, I will show the following: if there exists a matching which plans strictly more dates than the schedule the algorithm has, then there exists an augmenting path in the network, meaning that the algorithm will find an improvement step. So the algorithm will only terminate when the schedule it has, consists of the maximum-possible number of dates.
We will prove the following: if the matching that the algorithm has is not yet optimal, then there is an augmenting path (so the algorithm will find a better matching before terminating). Consider the following example. Suppose the algorithm has a dating schedule indicated by red lines, which is not an optimal one because there is a better dating schedule indicated by blue lines.
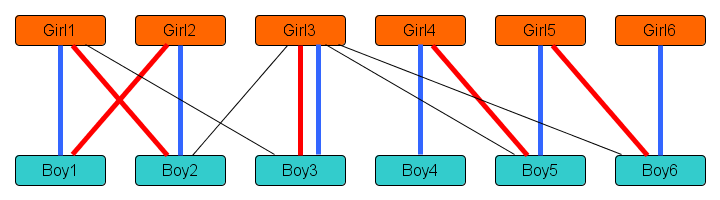
Note that the matching in red that the algorithm currently has consists of 5 dates, while the matching in blue is better since it consists of 6 dates. Let’s consider the difference between the red and the blue matchings: it consists of those dates that are planned by one of the two schedules, but not by both. It has the following network structure:
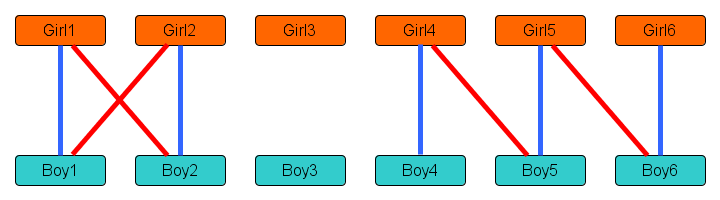
This network has a very limited shape: it consists of one cycle of 4 nodes on the left, and a path of six nodes between Boy4 and Girl6 on the right. This limited shape is not a coincidence. If you have two matchings in the same boy/girl network, then their difference network consists only of paths and cycles. Each node gets at most one partner from the red matching, and one from the blue matching; so in the difference network, each node touches at most two lines. A network where each node touches at most two lines, is easily seen to consist of separate paths and cycles.
In the example figure, the path from Girl6 to Boy4 forms an augmenting path: it connects a girl that is unmatched by the algorithm’s red schedule, to an unmatched boy, using a path whose lines alternate between being red (scheduled) dates and dates that the red schedule does not use. Let’s now see why it must always be true that if the red matching has fewer dates than the blue matching, there is an augmenting path to improve the red one.
We just reasoned that the difference network consists of separate paths and cycles. Note that a cycle in a boy/girl network contains an even number of lines: if you start at a girl and follow an odd number of lines, you always end up at a boy. So a cycle that starts at a girl and ends at that same girl, consists of an even number of lines. So every cycle in the difference network consists of an even number of lines, of which half are red and the other half are blue.
Since the number of blue lines is strictly larger than the number of red lines, there must be a component of the difference network that has more blue than red lines. This component cannot be a cycle, since we just argued that cycles have exactly as many red as blue lines. As the only possible types of components are paths and cycles, this means the difference network must have a path that has more blue than red lines, like the path from Girl6 to Boy4 in the example.
Now let’s think back to what that means: if the red matching, the one the algorithm is building, is not yet of maximum-possible size (because some larger blue matching exists, that the algorithm does not yet know about), then there is a path P in the difference network that has more blue than red lines. Since the colors alternate between red and blue on any path in the difference network, this means path P starts and ends with a blue line. In turn, that means that the endpoints of path P are nodes that have no partner under the red matching. Hence P is a path, starting an ending in nodes that are not matched by the algorithm’s red schedule, on which the lines alternate between potential dates and planned dates. So P is an augmenting path!
We have shown the following: as long as the algorithm’s matching is not yet optimal, there is an augmenting path. The post-it procedure on the oriented network will find such a path, which is used to find a schedule with more dates. When the algorithm terminates, there is no more augmenting path to be found, and therefore no matching exists that schedules more dates. So the algorithm’s output is optimal!
(If you follow the argument above closely, you will notice that the correctness proof relies on the fact that the network consists of boys and girls, with all potential dates between members of different sexes. Unfortunately, this means that the algorithm does not work in networks with same-sex dates. That turns out to be a more difficult algorithmic problem. There are efficient algorithms to solve it, but they are significantly more complicated. The flowers-and-blossoms algorithm by Jack Edmonds can be used to solve it.)
Final words
Congratulations, you have now learned how the augmenting-paths algorithm works and how efficient it is. Moreover, you have seen why it works, and how mathematics can be used to prove that! You can be confident that if you ever find yourself in charge of the Valentine’s night committee, you can efficiently find the optimal schedule to foster everyone’s budding romance. If you know some computer programming, then the ideas about drawings and post-its in the explanation above can easily be turned into code in your favorite programming language. Try it if you feel up to the challenge!
A mathematician once told me that problems that are very simple to state can be very deceiving, and sometimes turn out to be extremely difficult to solve. One such problem was the Four Color Problem.
It is safe to say that traveling impacts the peak performance of teams and athletes in general - studies have been done across all kinds of sports that confirm this intuitive idea. Thus, to avoid unfair- and unhappiness, an organizer should aim to minimize the effect of travel time disparities.
This is a question I have been thinking about for the last two years. In this article, I will give a little overview of what I have discovered in that time.
During the last decades, many resources have been invested in quantum computing. This research field has grown immensely and amazing results have been obtained. The plans for the future are highly ambitious, but at the same time, there are serious questions that need to be addressed.
In Part 1 Jackie explained to her fried Sam how the problem of picking a card from each of the 13 piles so that there is exactly one card with each rank translates to a problem on bipartite graphs. The mathematical problem asks you to find a perfect matching in a regular bipartite graph.
