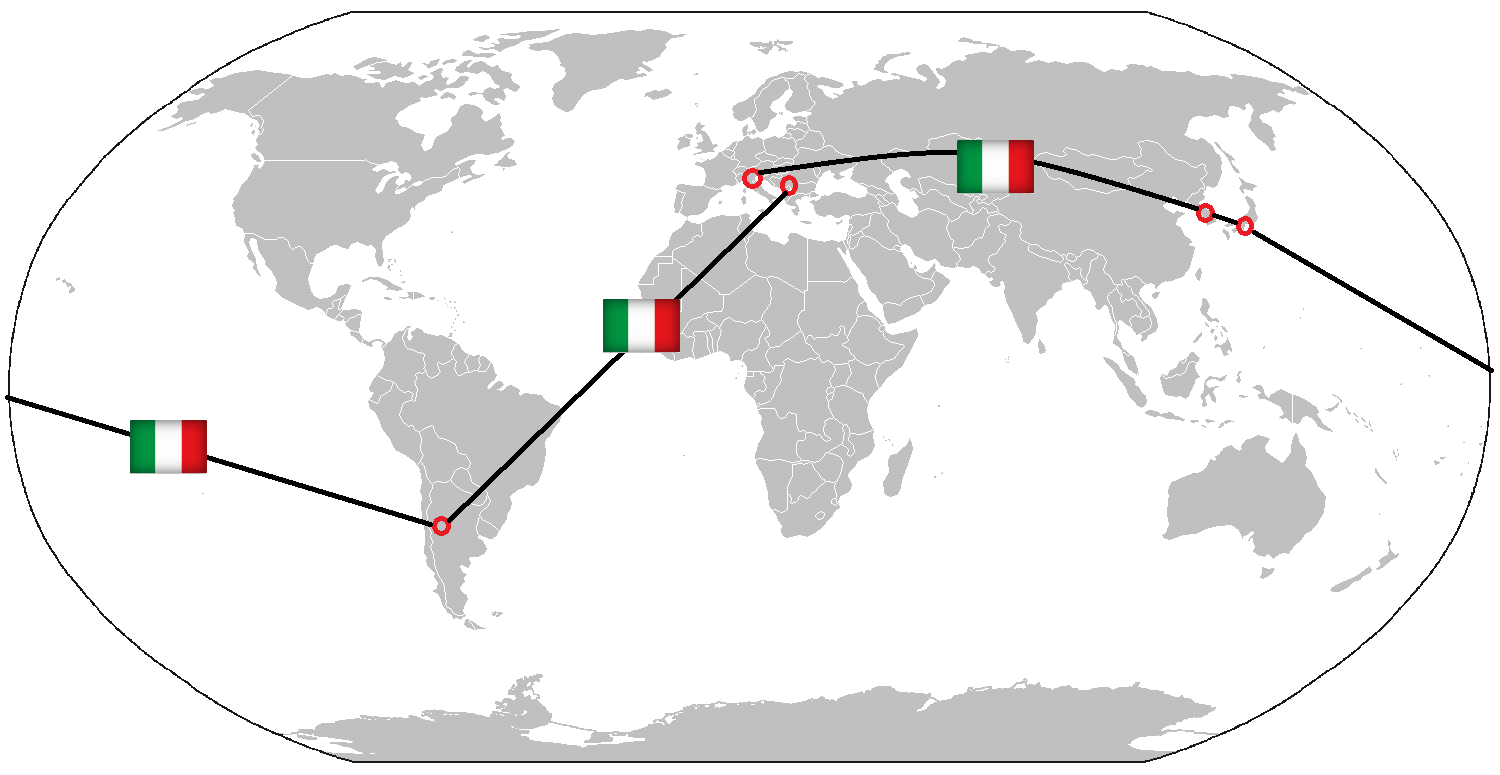
It is the beginning of June 2018, when the Italian men's volleyball squad wins the first 3 matches of the inaugural Volleyball Nations League, beating Germany, Brazil, and Serbia within one weekend in Serbia. The Italian team, however, did not have time to celebrate the victory much - the next weekend they had to play in Argentina, after that in Japan and South Korea, to end the month playing in Italy again.
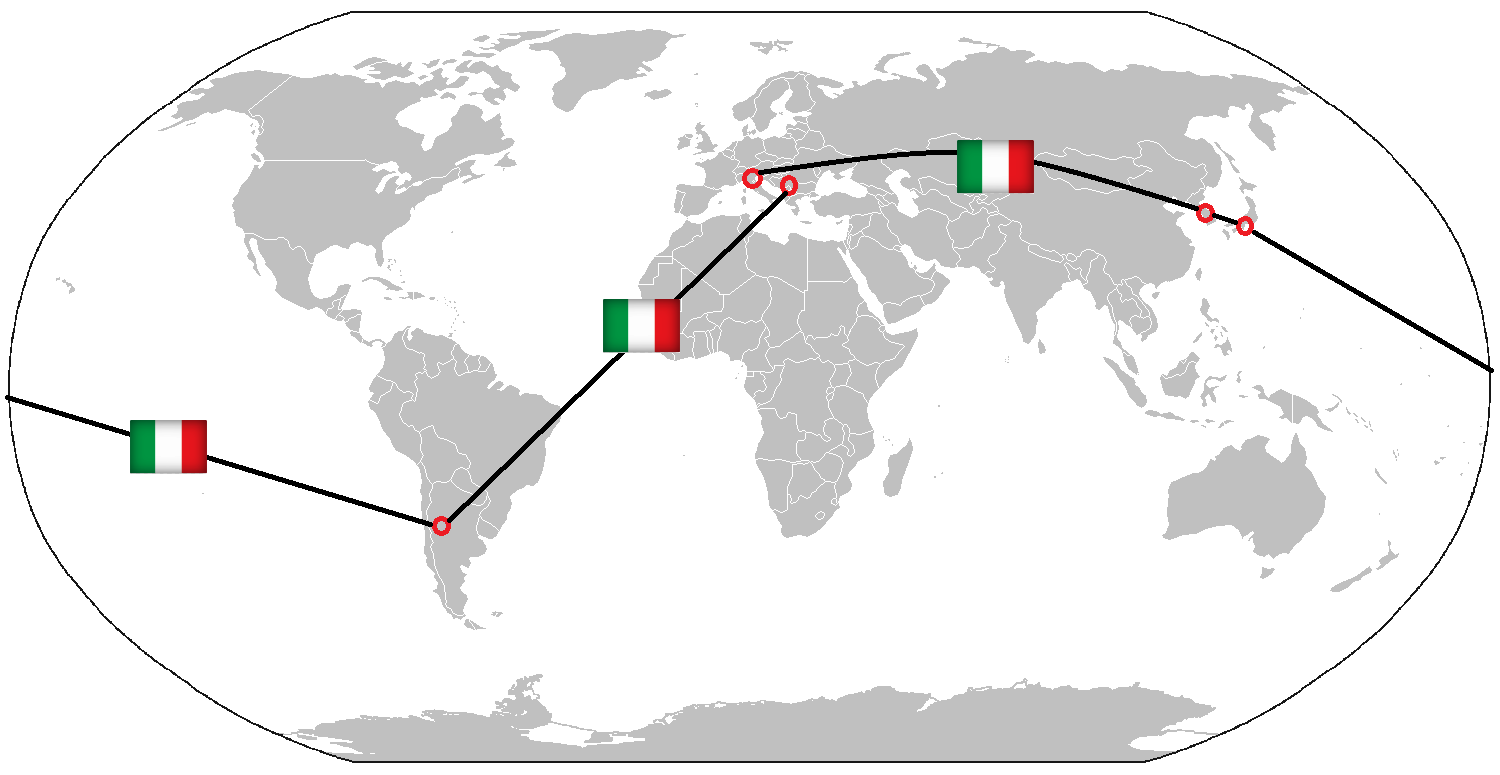
Italy had to fly across the globe in four weeks.
Flying across the globe in four weeks, had its toll on the team and they eventually finished 8th, winning only 4 out of 12 matches after the first round. In contrast, the team on top of the table at the end of the competition was France, who never had to leave Europe for their matches.
A few weeks later the French team failed and the Italians succeeded in qualifying for the final rounds of the World Championships, which was organized without much traveling between matches.
Fairness is not evident
It is safe to say that traveling impacts the peak performance of teams and athletes in general - studies have been done across all kinds of sports that confirm this intuitive idea. Thus, to avoid unfair- and unhappiness, an organizer should aim to minimize the effect of travel time disparities.
If we look at the Volleyball Nations League (VNL), this has a set-up that is very prone to be influenced by jet lags. There are 16 teams, who play in 5 consecutive weeks, where every week all teams are divided into four groups of 4, in such a way that all teams meet each other exactly once; such a tournament, where every participant plays everyone else once is called Single Round Robin.
The group stages are played in different venues anywhere on earth, so there are 20 different locations used to host the groups. To participate in the competition, teams may have to travel all around the world to play, with only a limited time to rest. In the table below, the groups of the Italian team during the Men's 2018 tournament are shown - notice how they meet all of their opponents exactly once!
Week 1
Week 2
Week 3
Week 4
Week 5
Location
Serbia
Argentina
Japan
South Korea
Italy
Opponents
Brazil
Argentina
Bulgaria
Australia
France
Germany
Canada
Japan
China
Russia
Serbia
Iran
Poland
South Korea
USA
Table: The groups of Italy in the Men's VNL 2018 tournament.
Can we create a schedule that is better and fairer to the teams, compared to the example given above?
Measuring fairness
To answer how we can do better, we first must think of: What is better? For a particular team, having a jet lag is only unfair if your opponent has no jet lag, and similarly, not having a jet lag is only beneficial if the other team does have one. We can write this down more formally to say something about the fairness of an entire schedule, using an example of the Men's VNL 2018.
In this tournament, Germany () and China () met in week 2, to play their fourth match, in Poland. The Germans previously played in Serbia and the Chinese played in China. After the first weekend, the Chinese had traveled 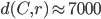kilometers, whereas the Germans only needed to cover 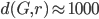kilometers.
The absolute difference in traveled distance, denoted by 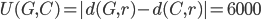can proxy as a measure of unfairness. The total unfairness of a schedule would simply be the sum 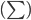of this unfairness for all matches, which results in 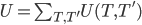. The VNL 2018 tournament had 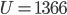in units of 100 km. Instead of distance, you could also look at travel time or differences in time zones, as a proxy, but we chose to keep it simple.
Optimal schedule
This 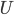is a useful measure for organizers to check how unfair their schedule approximately is, but how can they apply it in general? Obviously, you want the best possible schedule, but to find this schedule in a Round Robin over 16 teams is difficult, even when using a computer. The number of possible schedules is just too large to simply check them all and pick the best one.
Luckily, there is a trick we can apply.
Every round the teams are divided into 4 groups of equal size, and each group is located in one venue. If we look at the Italians starting group, numbered Group 4, from the Men's VNL 2018, that consisted of Italy, Germany, Serbia, and Brazil. They all played each other in that round and did not meet each other in the next rounds.
If we look at the second week, we see that Italy flew to Argentina, Brazil to Brazil, Germany to Poland and Serbia to Bulgaria. All four teams played in different groups! Coincidence? No.
As the teams can't meet again (it is a Round Robin tournament), they have to play in different groups. As there are four groups every week, there will be exactly one team from Group 4 in each of the groups next week. And this holds for every group, every week.
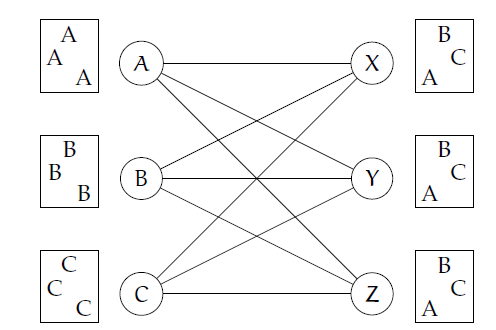
Trick: Two teams are never in the same group twice.
If we look at this from the viewpoint of a venue, we see that we get visitors from all venues in the preceding rounds. Indeed, all of the venues 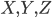see that teams from 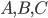will arrive. Thus, without knowing which specific teams this will be - Italy, Germany, Brazil, Serbia, etc. - we know the unfairness of the games that will be played in that group, as we know the distances traveled to that group.
In other words, we can determine the unfairness of a schedule without knowing the complete schedule. We only need to know part of the schedule, namely which venues are used in every round - if we know this, we know everything we want to know. Optimizing this is a much simpler problem and is way easier to calculate.
Interestingly, the observation that we only need to know the venues per round holds for any round-robin tournament that has a group size equal to the number of groups - besides the VNL, every group in the EURO 2020 group stage can be seen as an example, as every group had two stadiums for two matches per round.
Improving the VNL 2018 schedule
Using this observation, we can search for better schedules. There are some additional constraints, such as countries wanting to play at home when their venues host a group. These constraints are not difficult to take into account, and importantly, have no influence on the validity of our choice to first schedule the venues.
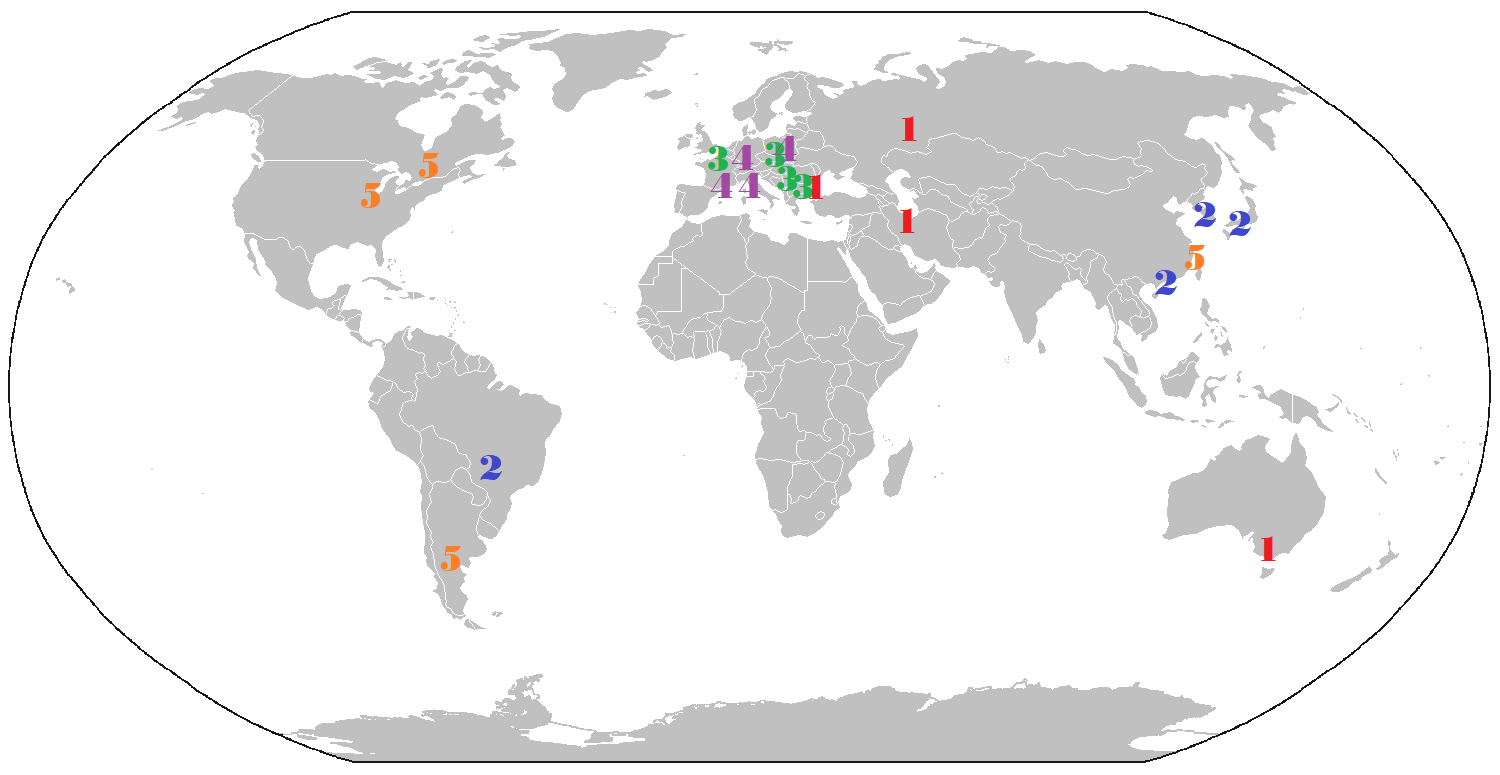
Optimal venue-assignments for Men's VNL 2018
Optimizing the venue assignment with respect to 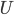, leads to a schedule with a 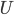equal to 233! The schedule used in practice had a 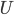of 1366 - roughly a factor 6 worse. The optimal venue assignment is shown in the figure above - there are weeks and for every week we see the 4 venues that are chosen to host a group. We leave it as a puzzle for the readers to convince themselves why this venue assignment is fairer than the one used in practice.
One might think that a newly proposed schedule would increase the total travel times - from a climate/cost perspective also something organizers should try to minimize - but this is not the case; while we can improve travel fairness by a huge margin, the total traveled distance does not increase significantly.
Of course, this leaves room for discussion. Not all travel distances are equal - jet lag can be a bigger factor than just the trip itself, for instance. This can be incorporated, however, as the reader/organizer pleases. Everything that is needed to create schedules this way that best satisfies the fairness around traveling, is a distance matrix. It is possible to "$$ any possible trip and use those scores to fill the matrix. For our example, we chose to score trips by their global distance, but something more sophisticated would work as well.
And it gets better. As we specifically did not create an entire schedule, as an organizer one can tweak the schedule to fit additional needs even more. As long as the venues are fixed to give optimal fairness, there is still plenty of wiggle room to cater to the fans, hosts and teams needs and wishes.
All in all, for this problem, we showed how a seemingly difficult problem could be untangled into two phases, one phase of scheduling venues and a phase of scheduling nations. By doing this, the fairness objective we set simplified as well, and could be solved completely in the first phase! And in this way, fans can enjoy nice volleyball and no more jet lags will influence the results!
The Premier League of Darts is an annual competition where the best darts players of the world compete over several months for the title, and the prize of £275.000. However… the schedule chosen by the PDC is unbalanced: some matches between pairs of specific players will occur relatively often, while others will occur very rarely.
Every January, the best chess players in the world compete in the TATA Steel Chess Championship, organized in Wijk aan Zee (The Netherlands). Among this year’s fourteen participants were Magnus Carlsen, world no. 1, coming into the tournament with an unbeaten streak of 104 matches, and Fabiano Caruana, the world no. 2.
It is the beginning of June 2018, when the Italian men's volleyball squad wins the first 3matches of the inaugural Volleyball Nations League, beating Germany, Brazil, and Serbia withinone weekend in Serbia. The Italian team, however, did not have time to celebrate the victory much - the next weekend theyhad to play in Argentina, after […]
In times of war, secure communication can be the difference between life and death, or even winning or losing a war. The first to patent a rotor machine in Europe was Arthur Scherbius in 1918. Scherbius’ version of the rotor machine became a commercial success, unlike the other patented machines. Scherbius named his machine Enigma.
On a quiet afternoon, professor Meth is working in her office in Leiden on some tantalizing mathematics problems. Suddenly, someone knocking on her door nervously disrupts the silence.
) and China (
) met in week 2, to play their fourth match, in Poland. The Germans previously played in Serbia and the Chinese played in China. After the first weekend, the Chinese had traveled 
kilometers, whereas the Germans only needed to cover 
kilometers.
can proxy as a measure of unfairness. The total unfairness of a schedule would simply be the sum 
of this unfairness for all matches, which results in 
. The VNL 2018 tournament had 
in units of 100 km. Instead of distance, you could also look at travel time or differences in time zones, as a proxy, but we chose to keep it simple.
is a useful measure for organizers to check how unfair their schedule approximately is, but how can they apply it in general? Obviously, you want the best possible schedule, but to find this schedule in a Round Robin over 16 teams is difficult, even when using a computer. The number of possible schedules is just too large to simply check them all and pick the best one.
see that teams from 
will arrive. Thus, without knowing which specific teams this will be - Italy, Germany, Brazil, Serbia, etc. - we know the unfairness of the games that will be played in that group, as we know the distances traveled to that group.
and for every week we see the 4 venues that are chosen to host a group. We leave it as a puzzle for the readers to convince themselves why this venue assignment is fairer than the one used in practice.
"$$ any possible trip and use those scores to fill the matrix. For our example, we chose to score trips by their global distance, but something more sophisticated would work as well.
