Every January, the best chess players in the world compete in the TATA Steel Chess Championship, organized in Wijk aan Zee (The Netherlands). Among this year’s fourteen participants were Magnus Carlsen, world no. 1, coming into the tournament with an unbeaten streak of 104 matches, and Fabiano Caruana, the world no. 2.
The championship was organized using a single round robin format, meaning that each player meets each other player exactly once. Thus, in total 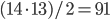matches were played over 13 rounds of 7 matches, in little more than two weeks. At the end of the tournament, it was Caruana who had collected the most points, winning 7 of his 13 matches and losing none of them. Clearly, this is a great achievement and a very impressive performance. Here, however, we argue that the schedule that was used during the tournament, may have helped him achieving this win.
A full playing hall in Wijk aan Zee. | Photo: Alina l'Ami/Tata Steel Chess, taken from chess.com.
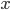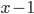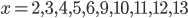A remarkable property of the schedule that was used is the following: the opponent of Caruana in round , had played Carlsen in the previous round , for . Thus in 10 of the 13 rounds, Caruana played someone who just had faced Carlsen the previous day. This phenomenon is an example of a carry-over effect taking place from Carlsen to Caruana. This is relevant, since one might reasonably argue that an opponent, just having played Carlsen, is, in his next match, somehow affected by having just played the world champion. Either by being mentally tired of the effort needed, or by being relieved not being beaten – the point is that the previous match typically has major impact on the next match. In this case, when asked about it, former world no 4 Peter Svidler commented this to be ‘very beneficial’ and that there was no doubt an advantage for Caruana to ‘pick up’ Carlsen’s opponents the next day.
During the tournament there was a high carry-over effect from Carlsen to Caruana due to the drawing.
A schedule where (nearly) all your opponents have faced the same player in the previous round, can lead to biased outcomes. This bias is a result of the described carry-over effect from player A to player B, which occurs if player A plays some player C in round 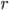and B plays C in round 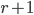. In fact, to each schedule, we can associate a carry-over matrix, that captures the exact number of times player A gives a carry-over effect to player B. In Figure 1, this matrix is shown for the TATA Steel Tournament.
Figure 1: Carry-Over matrix corresponding to the TATA Steel chess tournament
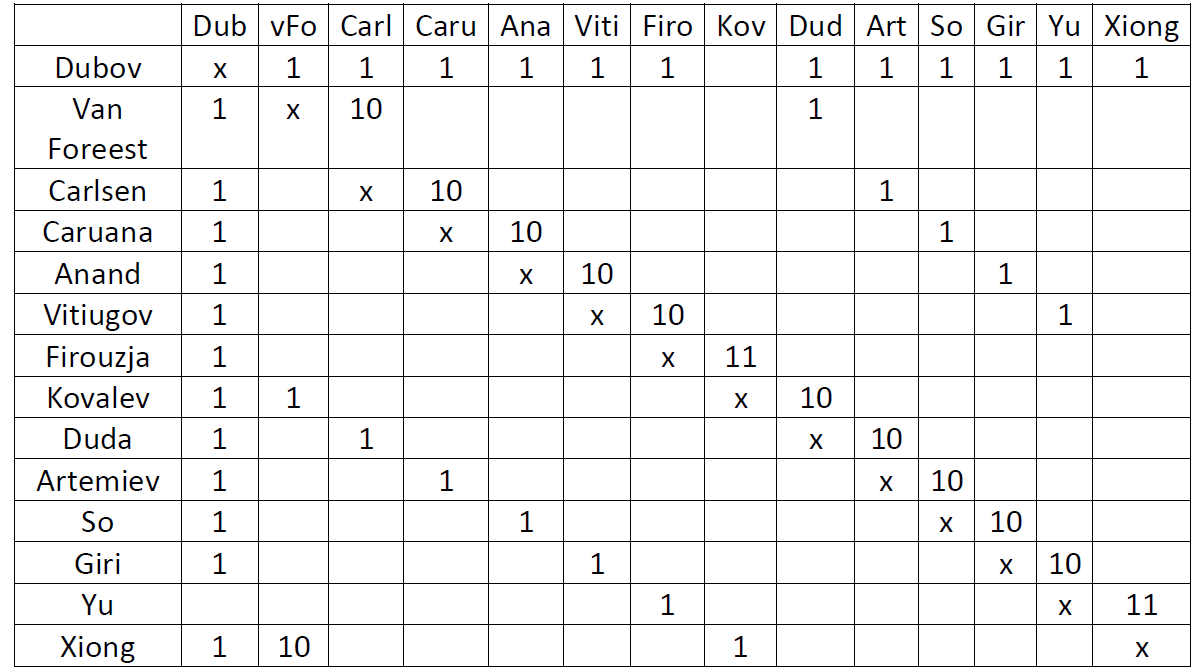
A balanced schedule would have every player receiving carry-over from every other player once; clearly, this schedule (see Figure 1) is not balanced. To measure the degree of “balancedness” of a carry-over matrix, Russel (1980) defines the so-called COE-value as the sum of the squares of the entries of the carry-over matrix. Clearly, the lower the COE-value, the more balanced the schedule is. For the matrix in Figure 1, the COE value equals 1378.
It is not a coincidence that the COE-value of the schedule is high; the reason is that the schedule is created via the Circle Method. See Figure 2 for an illustration of this method. This is a simple and elegant method to generate a valid schedule in which each player meets every other player exactly once. Because of its simplicity it is one of the most frequently used methods to construct round robin schedules, and (for chess) it has the nice property that one can assign black and white pieces for each round such that each participant plays the black and white pieces in a mostly alternating fashion.
However, as shown by Lambrechts et al. (2018), this method actually guarantees that a schedule with a maximum COE-value is generated!! Thus, to avoid bias among the participants, this is not a desirable schedule at all.
Round 1 of TATA Steel chess tournament
Round 2 of TATA Steel chess tournament
Round 3 of TATA Steel chess tournament
Figure 2: Illustration of how the Circle Method was used to generate the schedule of the TATA Steel chess tournament. Dubov is fixed at the top position of the left-most board. All other players shift their position in clockwise order after each round. The left-most board alternates black-white while all other boards stay fixed. To see the carry-over effect from Carlsen to Caruana, note that in both rounds 2 and 3 Caruana’s opponent played against Carlsen in the previous round. And in fact, all players except Dubov (and Carlsen and Caruana) play against Carlsen the round before they play Caruana.
A popular argument in favor of the perceived fairness of a schedule like the one used in the TATA Steel Chess Championship is that a random draw is used to assign the chess players to the positions (see Figure 2). Since every player has the same probability for receiving any particular position, the resulting schedule is deemed fair. We disagree.
An equal probability for any (dis)advantage prior to the schedule, does not erase the (dis)advantage once the schedule is made up. As explained in Figure 2, the schedule used in the TATA Steel Chess Championship ensures that “bad” schedules arise, i.e., it is guaranteed that such schedules have a high carry-over effect value. Other schedules exist that are much better, and, in our opinion, should be used to construct a schedule.
The following schedule (see Figure 3), found with a technique called integer programming, has a COE value of only 344; moreover, the players play white and black alternating in all but one round, in the same way as in the schedule constructed with the circle method.
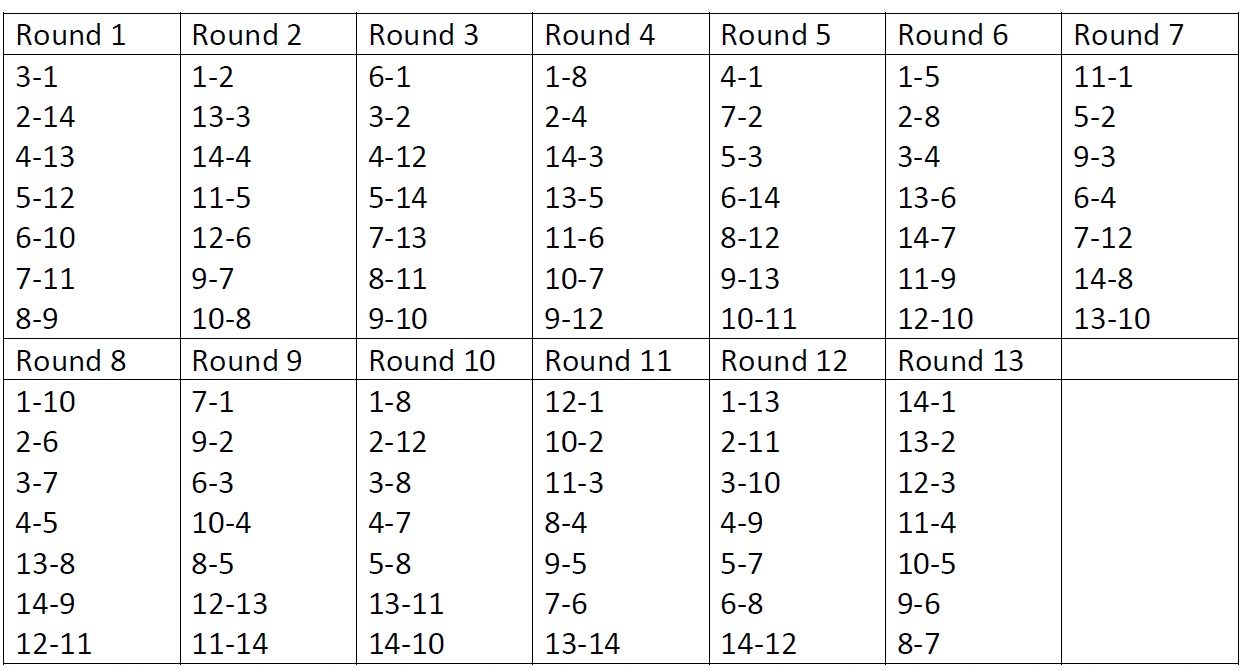
In this scheme no player gives a carry-over more than 4 times to any other player, and, as mentioned above, the COE value is 344 – significantly lower than the 1378 of the schedule that was used in the tournament.
Concluding, in round-robin competitions where there is a possibility of a match affecting the next match, schedules generated by the Circle Method run the risk of leading to biased outcomes. Alternative schedules exist and should be used instead.
Reference:
E. Lambrechts, A. Ficker, D. Goossens, and F.C.R. Spieksma (2018), Round-robin tournaments generated by the Circle Method have maximum carry-over, Mathematical Programming 172, 277-302.
The Premier League of Darts is an annual competition where the best darts players of the world compete over several months for the title, and the prize of £275.000. However… the schedule chosen by the PDC is unbalanced: some matches between pairs of specific players will occur relatively often, while others will occur very rarely.
It is safe to say that traveling impacts the peak performance of teams and athletes in general - studies have been done across all kinds of sports that confirm this intuitive idea. Thus, to avoid unfair- and unhappiness, an organizer should aim to minimize the effect of travel time disparities.
It is the beginning of June 2018, when the Italian men's volleyball squad wins the first 3matches of the inaugural Volleyball Nations League, beating Germany, Brazil, and Serbia withinone weekend in Serbia. The Italian team, however, did not have time to celebrate the victory much - the next weekend theyhad to play in Argentina, after […]
Trust is required when we buy a used car from a personal connection or via-via. When we vote for a politician we trust that they will act in our favour. In this article we will explore how Game Theory is used in attempts to model trust and cooperation.
In the vibrant city of Bangalore, India, the International Centre for Theoretical Sciences (ICTS) played host to a discussion meeting titled "Challenges in Networks" from January 29 to February 2, 2024.
matches were played over 13 rounds of 7 matches, in little more than two weeks. At the end of the tournament, it was Caruana who had collected the most points, winning 7 of his 13 matches and losing none of them. Clearly, this is a great achievement and a very impressive performance. Here, however, we argue that the schedule that was used during the tournament, may have helped him achieving this win.
, had played Carlsen in the previous round 
, for 
. Thus in 10 of the 13 rounds, Caruana played someone who just had faced Carlsen the previous day. This phenomenon is an example of a carry-over effect taking place from Carlsen to Caruana. This is relevant, since one might reasonably argue that an opponent, just having played Carlsen, is, in his next match, somehow affected by having just played the world champion. Either by being mentally tired of the effort needed, or by being relieved not being beaten – the point is that the previous match typically has major impact on the next match. In this case, when asked about it, former world no 4 Peter Svidler commented this to be ‘very beneficial’ and that there was no doubt an advantage for Caruana to ‘pick up’ Carlsen’s opponents the next day.
and B plays C in round 
. In fact, to each schedule, we can associate a carry-over matrix, that captures the exact number of times player A gives a carry-over effect to player B. In Figure 1, this matrix is shown for the TATA Steel Tournament.
