The Premier League of Darts, which started February 3rd 2022, is an annual competition where the best darts players of the world compete over several months for the title, and the prize of £275.000.
The concept of the league changed drastically compared to the previous years – in this edition, every one of the 16 rounds is a knock-out tournament on its own. Every round, there will be a winner and importantly, in every single match there is something to play for, which should cause excitement. To enable this format, the number of players is reduced from 10 to 8, making the weekly knock-out compassing 4 quarter finals, 2 semis and one final.
The 16 rounds are structured in the following way: the first 7 rounds have a predetermined fixture, then there is a special round, again 7 rounds with a given fixture, and a last special round. The draw in the special rounds depend on the standings at that time. The other (regular) rounds have a fixed scheme, determined in advance by the Professional Darts Corporation (PDC). Our analysis focusses on the draws in these 14 regular rounds
The idea behind this new format is to have the best darters play against each other every week. As such, it is comparable to the Champions League in football, or the many play-offs that are employed at the end of top competitions – who doesn’t want to see the greatest players battle it out? However… the schedule chosen by the PDC is unbalanced: some matches between pairs of specific players will occur relatively often, while others will occur very rarely. In this article, we will illustrate the presence of this phenomenon, and we will give an alternative that solves this issue.
As described above, we analyze a situation where 8 players meet each other 14 times in a knock-out tournament. At first, we want every player to meet every other player twice in the first round (quarter final), to ensure diversity over the different matches. As there are in total 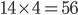quarter finals, and 28 pairs of players, this is possible - and indeed, in the schedule chosen by the PDC, the quarter finals are nicely divided over all possible couples in the current schedule.
However, which opponent a player can meet in the semi-finals, is not so nicely distributed. Of the 14 scheduled knock-out tournaments, 10 set up a potential semi-final clash between Scotsmen Peter Wright and Gary Anderson. On the other hand, Peter Wright can never meet Gerwyn Price in the semi-finals, and neither can James Wade meet Michael Smith in that stage of the competition, nor can Michael van Gerwen meet Gary Anderson. Exactly how many times a pair of players can meet each other in the semi-finals, is denoted in Table 1.
Table 1: Potential semi-final matches.
This unbalancedness is undesirable, for multiple reasons. First of all, as a player, it’s a nuisance since unbalanced schedules can be unfair. The fact that Michael Smith and Michael van Gerwen might meet each other 10 times in the semi-finals, has its influence on both their chances of reaching the final and qualifying for the end tournament. In addition, the fact that the two most recent world champions, Wright (current) and Price (former), will be able to avoid each other until the finals is something they won’t regret either – in the current schedule they cannot meet each other before the finals a total of 12 times. Thus, although everyone is trying to win the grand prize, not everyone’s path is equal, contrary to the previous editions of the PDC.
Secondly, as a viewer, one may wonder whether the current schedule leads to an exciting tournament. Of course, viewers want to see the best darters play against each other every week, but they may not want to see the same semi-finals and finals every week. The risk of seeing matches that are a repetition of previous ones is very high in the current schedule.
And these objections to the current schedule can be avoided. It is actually possible to schedule the players in such a way, that they still meet each other twice during all quarter finals, but also have exactly 4 potential meetings during the semis and 8 during the finals. There does exists a balanced schedule of the 14 rounds; the table analogue to Table 1 that belongs to such a balanced schedule, would be filled with entries of ‘4’.
To make such schedule, we use a mathematical concept called the Fano-plane, see Figure 2. We describe how to schedule the first 7 knock-out tournaments. First, give the players a number from 1 to 8. Then, from the figure beneath, pick a number and a color attached to the number, in such a way that all numbers (except 8) and all colors are picked exactly once.
Figure 2: Fano-plane.
When for example (2, red) is picked, that represents the knock-out tournament, in order of the bracket: 8-2, 1-5, 6-4, 7-3. Team 8 plays against the chosen number 2, the winner of that match plays a semi against the winner of the match between the other number on the chosen color, 1-5. On the other half of the schedule, the teams are matched that are on a line together with 2, so 7 plays 3 (light green) and 6 plays 4 (light blue).
This way, we can choose 7 rounds, for example ((1, purple),(2, red),(3, dark blue),(4, light blue),(5, orange),(6, dark green),(7, light green)). If we couple number to darters by the ordering used in Figure 1, this would result in the following first half of the competition:
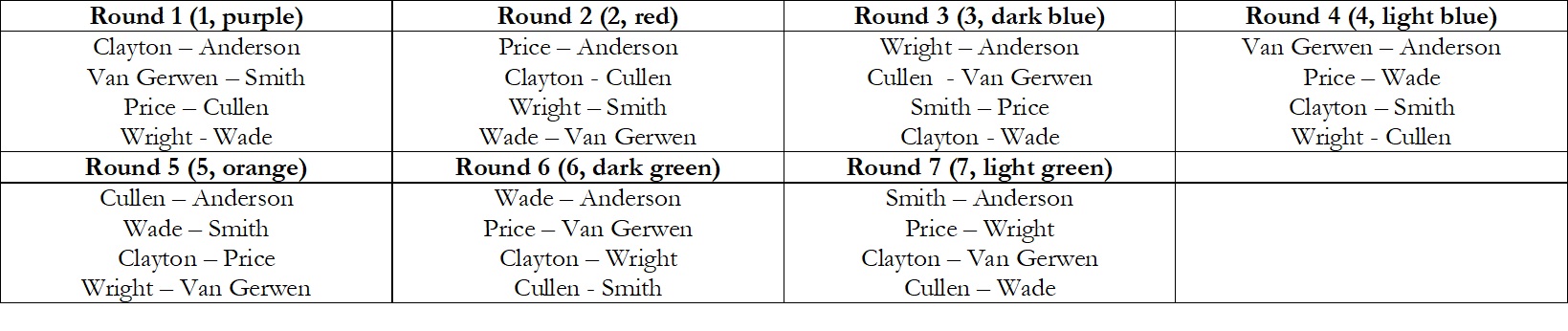
Figure 3: A balanced schedule.
This schedule can be repeated in the second half of the season – or another one can be created in a similar manner – and this way, every pair of players has exactly 2 meetings in the quarter finals, 4 potential meetings in the semis and 8 potential meetings in the final.
If the schedules would have been completely random, the expected amount of times a pair of players like Wright and Price could potentially meet each other in the final, would be 4 out of 7. Our solution nicely reaches that expectation for every pair of players in the 7 rounds. All that is left for the players to do, is to reach those finals…
It is safe to say that traveling impacts the peak performance of teams and athletes in general - studies have been done across all kinds of sports that confirm this intuitive idea. Thus, to avoid unfair- and unhappiness, an organizer should aim to minimize the effect of travel time disparities.
We want our guts to be filled with a diverse range of mutually beneficial and competitive interactions, a perfect blend of friends, frenemies, and enemies to keep our guts active and body on its toes. Read how networks can help understand these interactions!
It is the beginning of June 2018, when the Italian men's volleyball squad wins the first 3matches of the inaugural Volleyball Nations League, beating Germany, Brazil, and Serbia withinone weekend in Serbia. The Italian team, however, did not have time to celebrate the victory much - the next weekend theyhad to play in Argentina, after […]
About a year ago, I came across an interesting event organised by the Youtube channel 3Blue1Brown. In this article, I give a quick overview of how I joined this competition, chose the topic, and made the video.
Say you are living in Eindhoven and would like to spend a day in Amsterdam: what better way to get there than taking the train? Before your train departs, a whole logistic operation has taken place in the headquarters of the railway company to make this trip possible.
quarter finals, and 28 pairs of players, this is possible - and indeed, in the schedule chosen by the PDC, the quarter finals are nicely divided over all possible couples in the current schedule.
