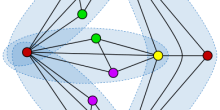
In previous article, we discussed what the degree sequence of a network or graph is. Recall that a graphical sequence is a sequence of degrees that can occur in a (simple) graph. Paul Erdős and Tibor Gallai developed a beautiful criterion to decide precisely when a degree sequence is graphical. In order to describe the Erdős-Gallai criterion, let us introduce some notation.
We denote the number of vertices in the graph by  , and number the degrees of the vertices by
, and number the degrees of the vertices by 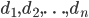 . This means that vertex 1 has
. This means that vertex 1 has 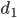 neighbors, vertex 2 has
neighbors, vertex 2 has 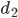 neighbors, etc. We may assume, as in part 2, that the degrees are ordered from large to small, so that
neighbors, etc. We may assume, as in part 2, that the degrees are ordered from large to small, so that 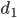 is the largest of the sequence
is the largest of the sequence 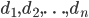 ,
, 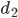 is the second largest, etc. The first requirement in the Erdős-Gallai criterion is that the sum of the degrees is even, this is the handshake lemma explained in part 1. The second requirement in the Erdős-Gallai criterion is a bit more involved. Let
is the second largest, etc. The first requirement in the Erdős-Gallai criterion is that the sum of the degrees is even, this is the handshake lemma explained in part 1. The second requirement in the Erdős-Gallai criterion is a bit more involved. Let  be an integer in between 1 and
be an integer in between 1 and  . Then, the Erdős-Gallai criterion requires that, for all such
. Then, the Erdős-Gallai criterion requires that, for all such  , the inequality
, the inequality
\begin{equation}
\label{Erdoes-Gallai}
\sum_{i=1}^k d_i \leq k(k-1) + \sum_{i=k+1}^n \min(k,d_i)
\end{equation}
holds. In words, if we sum the  largest degrees then this cannot be more than
largest degrees then this cannot be more than 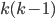 plus the sum of the minimum of
plus the sum of the minimum of 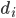 and
and  , summed over the vertices that do not have the
, summed over the vertices that do not have the  largest degrees.
largest degrees.
Let us work this criterion out in some examples. In part 2, we showed that the sequence (3,3,1,1) is not graphical. Take 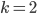 . Then, the left hand side of \eqref{Erdoes-Gallai} equals
. Then, the left hand side of \eqref{Erdoes-Gallai} equals 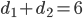 . Since
. Since 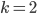 , we have that
, we have that 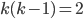 , while
, while 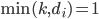 for
for 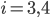 . Thus, the inequality in \eqref{Erdoes-Gallai} does not hold for
. Thus, the inequality in \eqref{Erdoes-Gallai} does not hold for 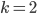 , as it should since (3,3,1,1) is not graphical. Note that the inequality is correct though for
, as it should since (3,3,1,1) is not graphical. Note that the inequality is correct though for 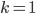 , as well as for
, as well as for 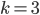 and
and 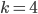 , so it is necessary to check the inequality for every
, so it is necessary to check the inequality for every  in between 1 and
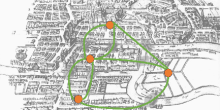
in between 1 and  . We leave it to the reader to verify that the Erdős-Gallai criterion indeed does hold in the simple graph on 7 vertices below:
. We leave it to the reader to verify that the Erdős-Gallai criterion indeed does hold in the simple graph on 7 vertices below:
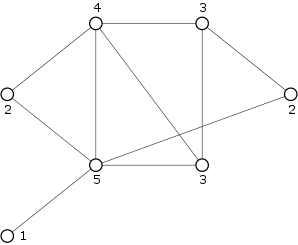
The Erdős-Gallai criterion looks a little mysterious. One way to see its relevance is to note that the term 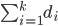 on the left hand side of \eqref{Erdoes-Gallai} equals the total degree of the first
on the left hand side of \eqref{Erdoes-Gallai} equals the total degree of the first  vertices in the graph. This total degree consists of the edges between themselves, of which there are at most
vertices in the graph. This total degree consists of the edges between themselves, of which there are at most 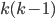 , together with the edges to the other vertices.
, together with the edges to the other vertices.
There can be at most  edges from any vertex
edges from any vertex 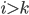 to the first
to the first  vertices. Also, there cannot be more than
vertices. Also, there cannot be more than 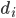 edges from
edges from  to the first
to the first  vertices. Thus, there can be at most
vertices. Thus, there can be at most 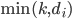 edges from
edges from  to the first
to the first  vertices, and summing this out over all vertices
vertices, and summing this out over all vertices  that are not in the first
that are not in the first  vertices gives that there are at most
vertices gives that there are at most
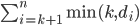
edges between the first  vertices and the other vertices. This shows that the Erdős-Gallai criterion in \eqref{Erdoes-Gallai} certainly needs to be true for any graphical sequence. However, it also sheds some light on how to produce a graph for any degree sequence that is graphical. If we can do this, then indeed the Erdős-Gallai criterion in \eqref{Erdoes-Gallai} ensures that the sequence
vertices and the other vertices. This shows that the Erdős-Gallai criterion in \eqref{Erdoes-Gallai} certainly needs to be true for any graphical sequence. However, it also sheds some light on how to produce a graph for any degree sequence that is graphical. If we can do this, then indeed the Erdős-Gallai criterion in \eqref{Erdoes-Gallai} ensures that the sequence 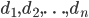 is graphical.
is graphical.
The proof that \eqref{Erdoes-Gallai} is really also necessary is more tricky, and will not be given here. However, we can illustrate how to construct a simple graph with the given degrees. We do this by connecting the edges one by one. Choudum [1] provides a proof by mathematical induction on the sum of the degrees: he lets 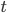 be the first index of a number in the sequence for which
be the first index of a number in the sequence for which 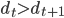 (or the penultimate number if all are equal), uses a case analysis to show that the sequence formed by subtracting one from
(or the penultimate number if all are equal), uses a case analysis to show that the sequence formed by subtracting one from 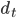 and from the last number in the sequence (and removing the last number if this subtraction causes it to become zero) is again graphic, and forms a graph representing the original sequence by adding an edge between the two positions from which one was subtracted.
and from the last number in the sequence (and removing the last number if this subtraction causes it to become zero) is again graphic, and forms a graph representing the original sequence by adding an edge between the two positions from which one was subtracted.
From a practical perspective, it is also of interest how one can obtain or create a graph with the given degrees when the Erdős-Gallai criterion gives that there is one. The Havel-Hakimi algorithm is a very simple way to produce such a graph. In this algorithm, one again orders the vertices according to their degrees as 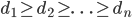 . Then, we connect the
. Then, we connect the 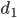 edges of the vertex with highest degrees to the
edges of the vertex with highest degrees to the 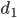 other vertices of maximal degree. Repeating this step (including the necessary reordering of the degrees) produces a simple graph precisely when the degree sequence is graphical. The Havel-Hakimi algorithm is thus is very simple implementation of the Erdős-Gallai criterion.
other vertices of maximal degree. Repeating this step (including the necessary reordering of the degrees) produces a simple graph precisely when the degree sequence is graphical. The Havel-Hakimi algorithm is thus is very simple implementation of the Erdős-Gallai criterion.
[1] Choudum, S. A. (1986), "A simple proof of the Erdős–Gallai theorem on graph sequences", Bulletin of the Australian Mathematical Society, 33 (1): 67–70, doi:10.1017/S0004972700002872, MR 823853.