The magic of mathematics ♠️♥️♣️♦️

Did you know that a city tour was the foundation of the mathematical field of graph theory? And that graph theory has applications even in magic? Before we show the magic lets warm up with a classical mathematical problem posed and solved by the great mathematician Leonard Euler in 1736.

Imagine you’re in a foreign country and you want to visit the capital city. There’s a river that divides the capital in different areas. To get from one area to the other, they build beautiful bridges which you all would like to see. But they’re still just bridges, so after crossing each bridge exactly once, you’ve seen enough. At the moment you’re at a really nice café, so you want to end your walk at the same spot as you are now, you want it to be a cycle.

Believe it or not, this problem was the foundation of an entire field of mathematics.

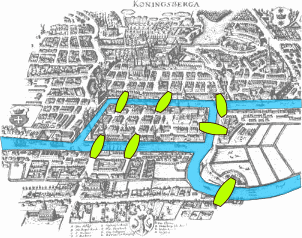
An old map of Königsberg with the seven bridges. Image By Bogdan Giuşcă - Public domain (PD),based on the image, CC BY-SA 3.0.

The roads connecting the bridges of Königsberg represented as a graph.

Mathematician Leonhard Euler wrote an article called “the 7 bridges problem” in which he tried to find a walk through the bridges of Königsberg. He drew a dot/node for each area, and a line connecting two points for each bridge connecting two areas. This collection of dots and lines is what we call a graph. If we draw arrows in the direction of the walk instead of lines, we call this a directed graph.

Euler found out that such a cycle, which he called an Eulerian cycle, that crosses each bridge exactly once, exists if and only if the graph is connected and there are equally many arrows going in each vertex as there are going out.

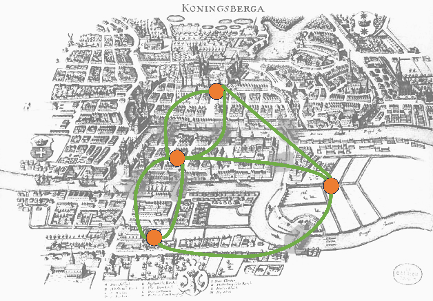
A connected graph is simply a graph that consists of one piece. Take a pencil and paper and draw two triangles, this is not a connected graph. If we now draw a line from a point of the first triangle to a point of the second one, then we do have a connected graph. Unfortunately, Euler proved that there is no Eulerian cycle possible in Königsberg. Try and figure out why it is not possible to find an Eulerian cycle in Figure 1a below. The fun in math is doing it yourself!

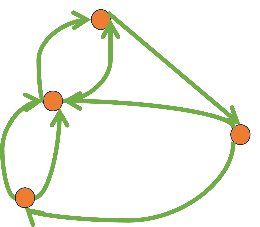
Figure 1a. There is no Eulerian cycle in Königsberg.

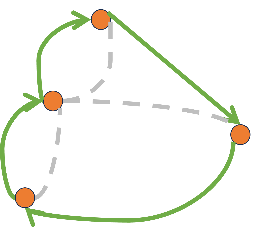
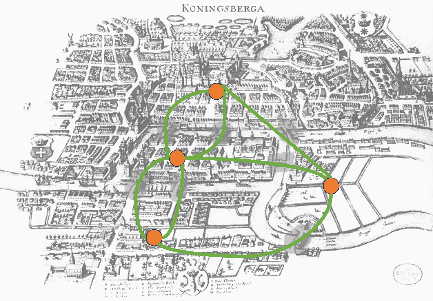
Figure 1b. If we remove three bridges, there is an Eulerian cycle.

Euler's theorem
An Eulerian cycle exists in a directed and connected graph.
$\Leftrightarrow$
An equal amount of arrows are going in each vertex as there are going out.

From bridges to magic

Although graph theory was born back in 1736, it keeps revealing wonderful results until today, and amazingly enough many of its magical aspects still remain hidden. Researchers are passionately trying to reveal them, making it a very vibrant area of modern mathematics. We will take you back to 1946, two-hundred years after Euler's discovery, and in the office of the Dutch mathematician Nicolaas Govert (Dick) de Bruijn, who in one of his mathematical discoveries managed to reveal some magic!

Try to imagine the following situation. You are in a classroom and you have eight cards. You let the cards go round and everyone is allowed to perform a cut of the deck. Next, three people pick the first three cards. Then you ask them to raise their hand if they have a red card. Would you believe it if I told you there is a way to always be able to guess the three cards, one for one?

This is a pretty cool trick on itself but using the magic of mathematics I will show you later on that this trick doesn’t only work for three people, but for any number of people you want. There are a few components to this magic trick:

the ordering of the cards such that cutting the deck doesn’t affect it,
a unique sequence of red and black cards,
and a "cheat sheet" to help you in the end.

Shuffling the cards

First, let’s have a look at what happens when someone performs a cut of the deck. Suppose the ordering of the eight cards is as follows (denote the red cards by 1 and the black cards by 0). Now suppose that we perform a cut of the deck with the two first cards.

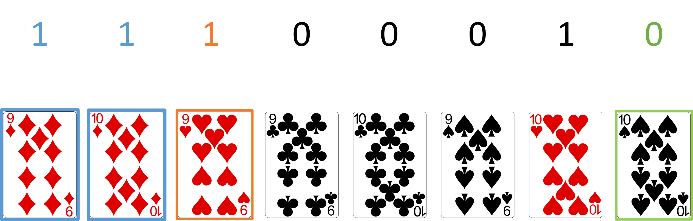
Figure 1a. Before cutting the deck.

Figure 1b. After cutting the deck.

This is exactly the same as shifting the starting position of our sequence by two. If we write the sequence on a toll then this would be the same as turning the toll two steps counterclockwise. As you can see, the order of the sequence hasn’t changed by shuffling the cards, the only thing that changed was the starting position on our toll.

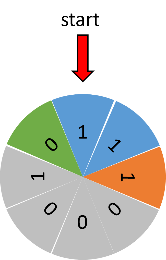
Figure 2a. Before cutting the deck.

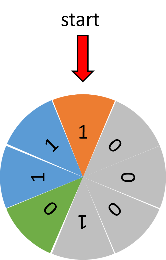
Figure 2b. After cutting the deck.

So cutting the deck does not "really" change the ordering of the cards. This can also be seen in the animation below. If you know the sequence, then you cut the deck a number of times, and you know the first card, then you know the whole sequence.

Figure 3: What changes is the first card, not their order.

Unique Sequence

Additional to not changing the red/black sequence while shuffling, we also wish to be able to directly figure out which specific cards the three people are holding. For this we need to take all the possible combinations of red/black in consideration. These are the different possible sequences of red/black of the three cards the people are holding. The first person can have a red or black card, which gives 2 possibilities. The second and the third person also have 2 different possibilities. Therefore, the total number of combinations would be 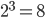$2^3=8$ , which was exactly the amount of cards that were passed through the class.

If we want to be able to match cards to a 0/1 sequence, 0 for a black card and 1 for a red card, we want the cards to be ordered in such a way that each possible combination of length 3 occurs only once in the ordering. Hence, we want a sequence of 0/1 that contains all different combinations, and contains them exactly once. An example of such a sequence is 11100010. Do you recognize this sequence from before?

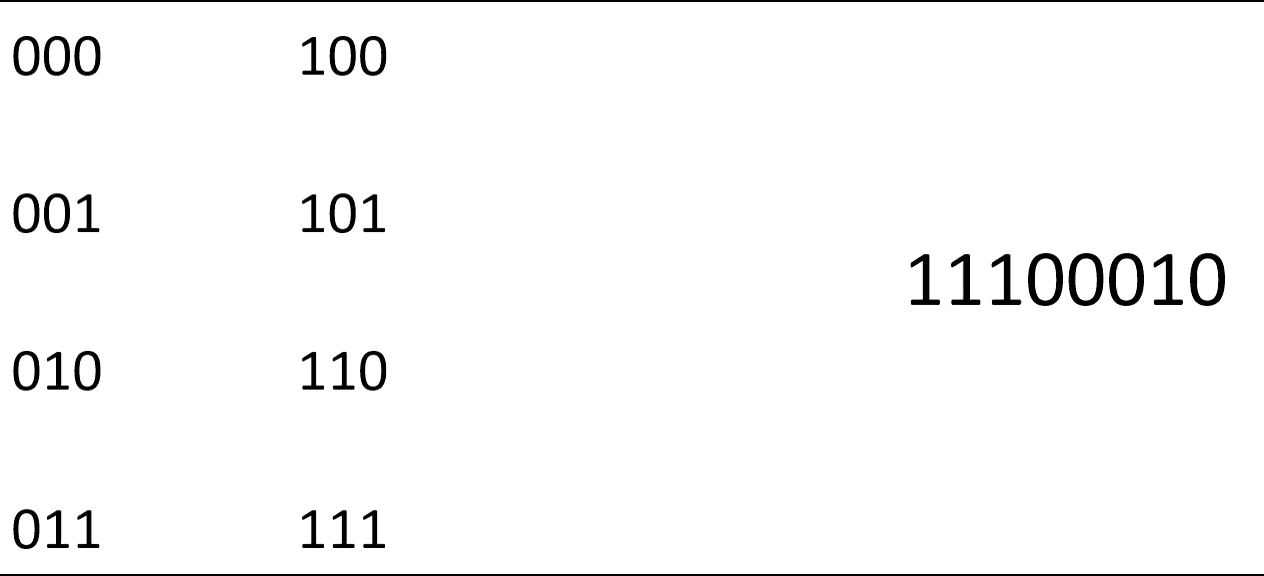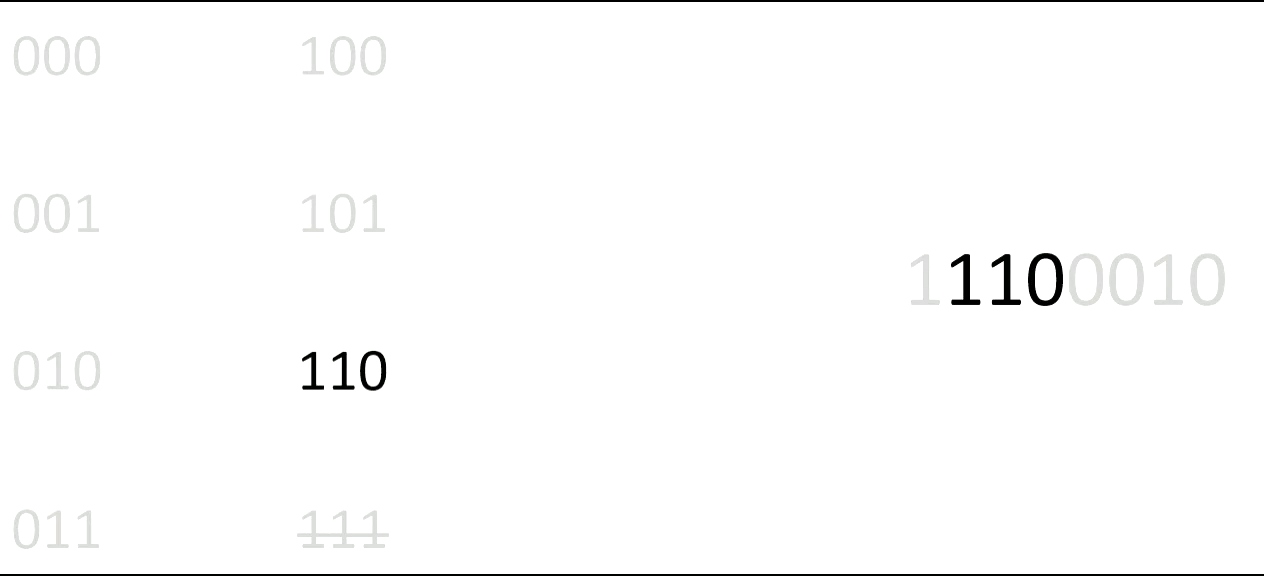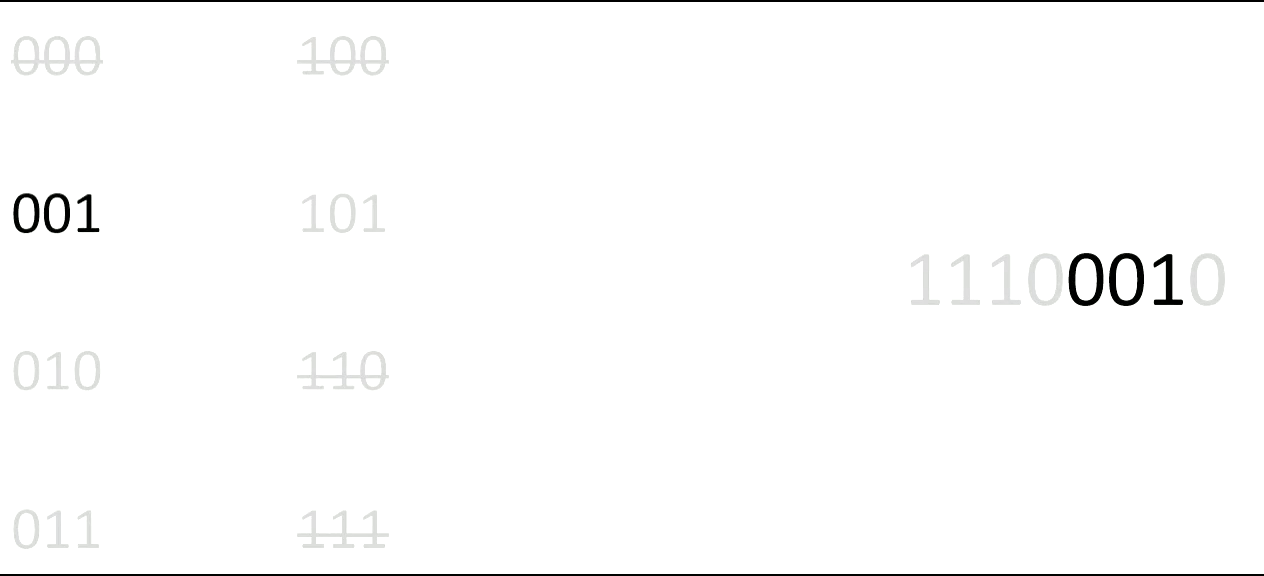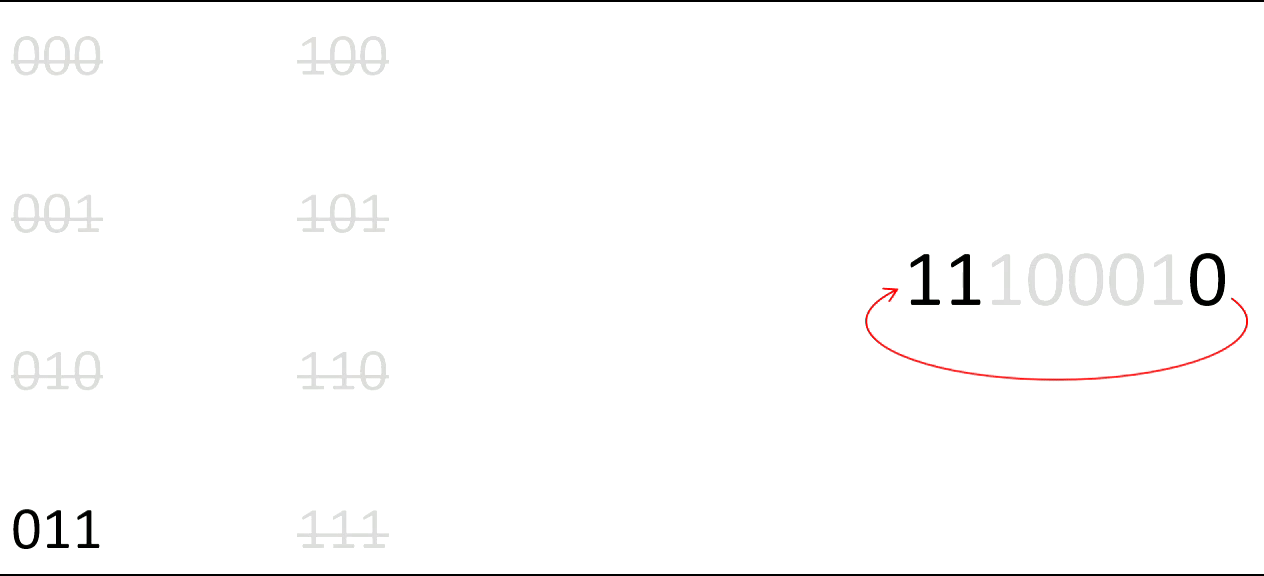
Figure 4: In the sequence 11100010 all possible combinations of 0/1 of length 3 appear. On the contrary, if you take the sequence 10101010 this does not happen.

Lets go back to the cards in Figure 1 and the magic trick. You have given these cards to eight people, after letting them cut the deck. Suppose that I know that the first person has a black card, the second person a red card and the third person a black card. Then this sequence is 010 and using the ordering above we know that the cards are 9 spades, 10 hearts and 10 spades. And by knowing this sequence you also know what everybody else has!

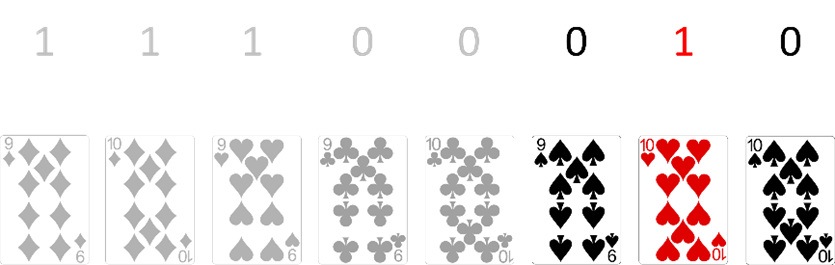
Figure 5: If you know the cards the last three people have, then you know what each one has!

So how would you perform this trick? First, order all the cards in the specific order shown above. Let the audience shuffle the deck by cutting it, let three people pick the cards and remember who took first, who second, and who third. Afterwards, let them rise their hand if they have a red card. Finally look at the cheat sheet to find out which cards they’re holding!

Figure 6: To perform the magic trick it is good to use a "cheat sheet" with the sequences.

You now understand the mathematics behind the trick, but mathematics has one more trick up its sleeve. This trick doesn’t only work for 3 people and 8 cards: it could be done with 5 people and 32 cards as well. Actually, if we extend the deck of cards in a particular way, the trick could even be performed with 10 people and 1024 cards. Just like Euler did when he went from a statement about bridges in real life to a general statement about Eulerian cycles in graphs, this trick can be generalized to an even more impressive mathematical statement: this trick is possible with 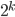$2^k$ cards and 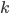$k$ people for each number $k$ !

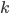Magic trick with the whole audience

As discussed before, the main ingredient of this trick was the existence of a sequence of 0s and 1s of length 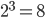$2^3=8$ , in which each 0/1 combination of length three appeared exactly one time. Such sequences are called de Bruijn sequences. We found a de Bruijn sequence for 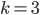$k=3$ , namely 11100010, or to put differently: for the situation where 3 people are involved. Thus, showing that this trick is possible is equivalent to showing that for each number of people, for each 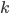$k$ , there exists a de Bruijn sequence of length $2^k$ .

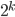The trick is possible with 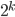$2^k$ cards and 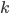$k$ people.
$\Leftrightarrow$
There exists a de Bruijn sequence for 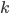$k$ .

De Bruijn graphs

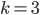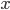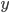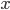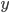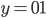To prove that a de Bruijn sequence exists, we use a special graph which is, not so surprisingly, called a de Bruijn graph. Its nodes for $k=3$ represent the different combinations of sequences of length 2. Draw an arrow from $x$ to $y$ if there exists a 0/1 sequence of length 3 with $x$ on its left and $y$ on its right. Take for example $x=00$ and $y=01$ , then 001 is a sequence with 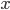$x$ on its left and 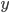$y$ on its right, hence we draw an arrow from 00 to 01.

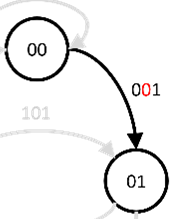
De Bruijn graphs have three beautiful properties.

They exists for all numbers $k$ .
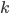They are always connected.
In each node of such a graph there is an equal amount of arrows going in as there are going out.

Hopefully this rings a bell: these are the conditions in Euler's theorem! Hence there exists an Eulerian cycle in each de Bruin graph! But what has an Eulerian cycle in a graph that, supposedly, was pulled out of thin air to do with our magic trick? Let’s look at the cards and find out.

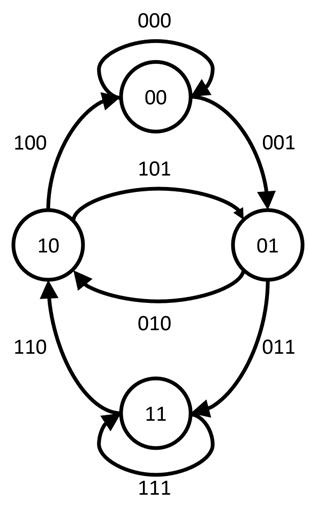
The first three cards had sequence 111. This is the same as the lowest arrow in the picture on the right. The next cards had sequence 110, this is the same as the arrow from 11 in de graph to 10. The next sequence, 100, is the same as the arrow from 10 to 00. If we keep doing this, we see that each arrow corresponds to a combination and once we finish we see that the last sequence is 011. Hence we are exactly back at our starting point. The Eulerian cycle in our de Bruin graph, corresponds exactly to a de Bruijn cycle!

Figure 7: A de Bruijn cycle yields the order of the cards!

We now are at the final part of our proof: there exists a de Bruijn graph for each 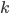$k$ , these are connected graphs, and there is an equal amount of arrows going in each node as going out of it. Therefore we know that there must be an Eulerian cycle in this graph. As Eulerian cycles in de Bruijn graphs correspond to de Bruijn cycles, we now know that de Bruijn cycles exist for each 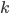$k$ . Hence we must conclude that the magic trick is possible for each amount of people. Isn’t that just wonderful? Enchanting? Magical? I’d like to welcome you in the fascinating world of mathematics.

This article was inspired by the really nice book "Magical Mathematics: the mathematical ideas that animate great magic tricks" by Persi Diaconis, Ron Graham, Martin Gardner. The magic trick is also described in this book.

Would you like to stay up to date when a new post appears on the Network Pages?

Subscribe to our mailing list