Degrees in graphs IV: degrees in large real-world networks
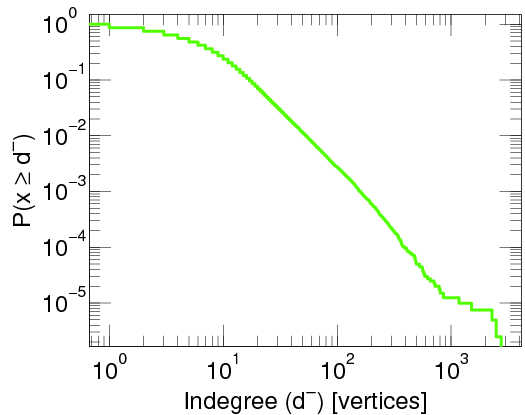
How are elements in real-world networks connected? That is the question we aim to answer in this post. Most real-world networks turn out to be extremely inhomogeneous.
Degrees in graphs III: Which degrees sequences are possible?
Paul Erdős and Tibor Gallai developed a beautiful criterion to decide precisely when a degree sequence is graphical.
Degrees in graphs II: Degree sequences
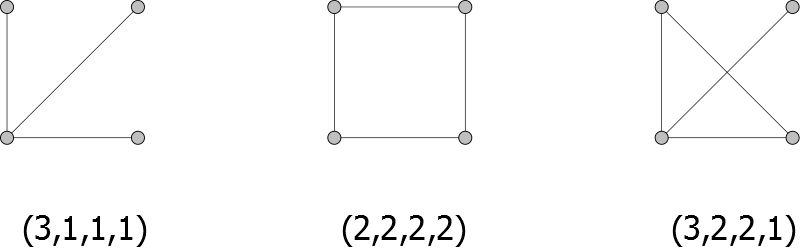
The degree sequence of a graph is the sequence of degrees of all its elements.
Degrees in graphs I: the Handshake Lemma
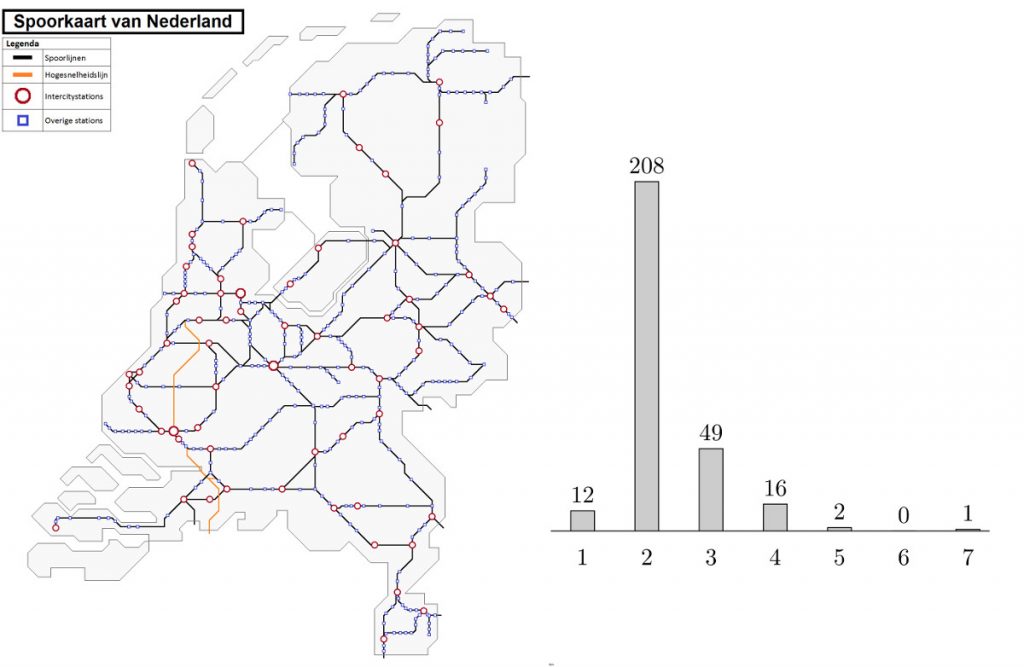
A graph consists of objects called vertices and connections between them called edges. For every vertex, we can count how many neighbors it has, which is called its degree.
