Random encounters with Ramsey numbers
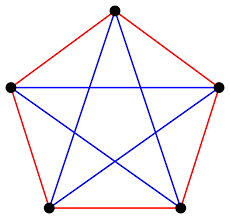
It is was the second time yesterday in a one week time and the fourth in a one month time that I came across Ramsey numbers. In the beginning I thought it was just a coincidence.
Wandering around the bridges!

Can you always find a route through the bridges? This is the question to be answered.
How to plan Valentine’s day using a matching algorithm
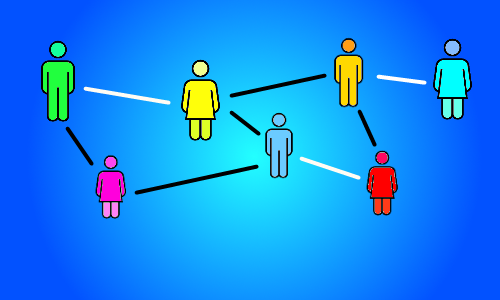
Finding a dating schedule that matches pairs of potential lovers up into dating couples, is an example of an algorithmic problem. There is a clearly defined input, given by the lists of who is considered an acceptable dating partner to whom. It is also clear what we want as the output: a pairing of classmates into acceptable boy-girl pairs that has as many pairs (dates) as possible. How can you find the best dating schedule?
Finding the shortest route to your holiday destination: Dijkstra's algorithm
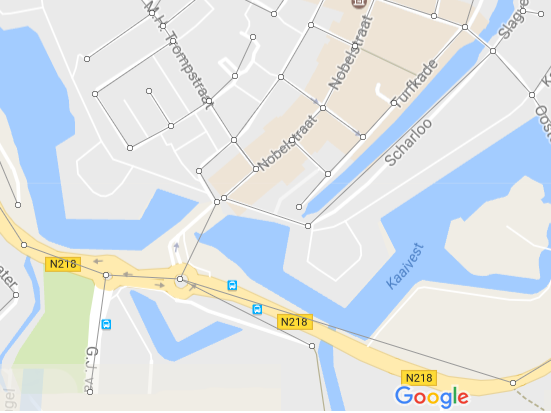
Nowadays we have route planners such as TomTom and Google Maps to make driving to a holiday destination a lot simpler. In this article we explain the science behind these route planners.
Degrees in graphs III: Which degrees sequences are possible?
Paul Erdős and Tibor Gallai developed a beautiful criterion to decide precisely when a degree sequence is graphical.
Network analysis of tax treaties
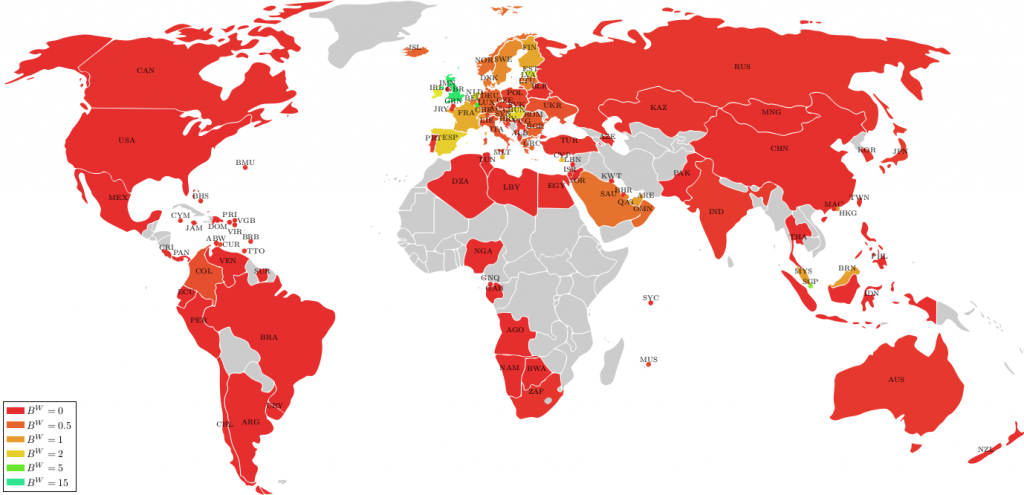
Large international companies often do not send their profits directly from one country to another. Instead, they send it via other countries, so-called conduit countries, to reduce the tax they pay. Which countries are the most important conduit countries?
Degrees in graphs II: Degree sequences
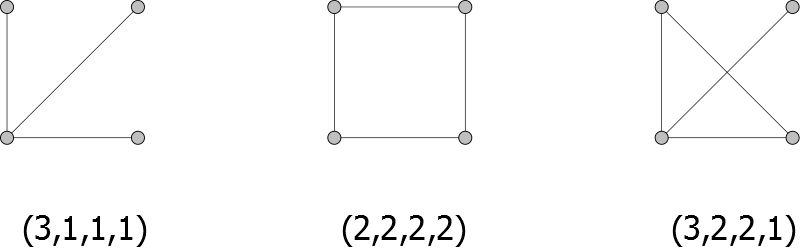
The degree sequence of a graph is the sequence of degrees of all its elements.
A Santa Claus network

Poor Santa has to travel all across the country to deliver all his presents. How does he do this?
Degrees in graphs I: the Handshake Lemma
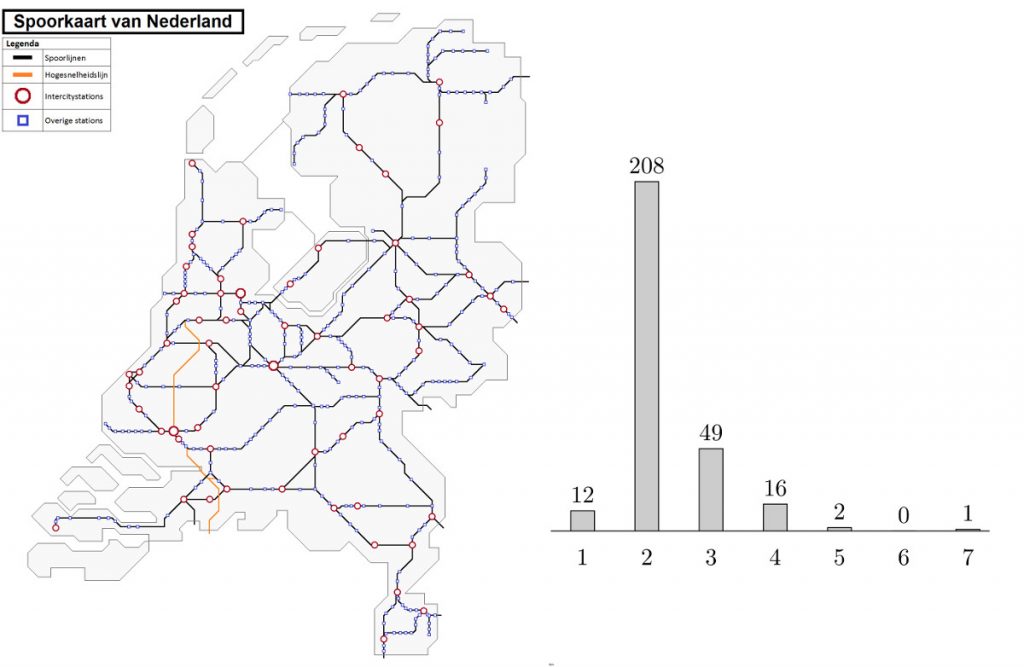
A graph consists of objects called vertices and connections between them called edges. For every vertex, we can count how many neighbors it has, which is called its degree.
A big breakthrough in the Graph Isomorphism Problem
The graph isomorphism problem asks the computer to see if two graphs (simple networks) can be made to look precisely the same if the computer is only allowed to slide the nodes and stretch the connections (so the computer is not allowed to draw or or erase nodes or connections).
