Random encounters with Ramsey numbers

It is was the second time yesterday in a one week time and the fourth in a one month time that I came across Ramsey numbers. In the beginning I thought it was just a coincidence.

Four coincidental encounters with these mysterious numbers, thought by Frank Ramsey around 1930. But today I realized that the last two events were not even close to a mere coincidence, recently there was a major unexpected breakthrough concerning Ramsey numbers mathematicians were waiting for fourteen years! And the news about it was everywhere.

First occurrence

Some time ago I attended a general audience talk of a colleague of mine who chose to talk about Ramsey numbers. The talk started with my colleague asking the following question to the public:

“Suppose that six people meet at a party. I argue that, whoever these six people are, there are always either three people who all know each other or there are three people who all don’t know each other.”

If you spend some time thinking about it you will see that the answer is easy if you suppose for example the trivial cases that all six people either know each other or they are strangers and all don’t know each other. But why does this hold whoever these six people are? If you spend some time on it you will for sure figure this out.

There is an elegant way to rewrite this problem as a combinatorial problem, namely, suppose you have six points and that they are all connected to each other. Suppose you color the edges either red or blue. Then in such a graph there always exists either a blue triangle or a red triangle. If there is no blue triangle there will definitely exist a red triangle and vice-versa! If you start drawing graphs with six points and blue-red lines connecting these points you will see that there is always a triangle (a triangle in a graph is what you expect it to be, three points connected to each other) whose edges are either all blue or all red. It is a little bit more challenging to find an argument why this holds. The following observation can help you find the argument.

Click here for a first observation

To come back to my colleague's statement about the party, say that each of the six guests is represented by one of the six points in the graph, a red edge between two points indicates that the two guests know each other, and a blue edge indicates that they don’t. This translation shows that the graph problem and the party problem are in essence the same.

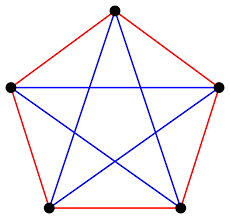
This statement does not hold if you consider less than six people/points. This is simple for the case of three or four people, what about five? Think of five people sitting on a round chair and each one only knows the one guest sitting on the left and the one on the right. Then each guest knows exactly two other guests who always don't know each other! You can also think of the colored graph on the right if you prefer a graph-version of this argument. The result I just sketched about parties and graphs corresponds to the Ramsey number 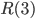$R(3)$ being equal to six. The Ramsey number 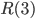$R(3)$ is thus defined as the minimum number of points needed so that every graph with this number of points, where the edges are colored blue or red, either has a blue triangle or has a red triangle! And this number is six. So $R(3)=6$ .

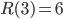The edges are blue or red and there is neither a blue nor a red triangle

Second encounter

The second encounter with Ramsey numbers happened when a student of mine had to give a presentation on this topic. You can see it as a coincidence in a broader sense. You are probably shaking from excitement to learn why these Ramsey numbers are so interesting, so let’s have a look at this. Intuitively the Ramsey number 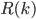$R(k)$ corresponds to the minimum number of guests you need to invite to a party to guarantee that there are either $k$ guests who all know each other or there are $k$ guests who all don’t know each other. Be careful, the Ramsey number says that in any group of people of this size this property should hold! Above we explained why $R(3)=6$ . In mathematics, the Ramsey number $R(k)$ is defined as the smallest number of points needed so that every possible graph with this number of points either has a so-called $k$ -clique or a so-called $k$ -stable set.

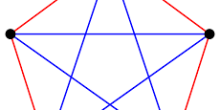
k - clique

In a graph a $k$ - clique is a collection of $k$ points such that all edges between these $k$ points are present.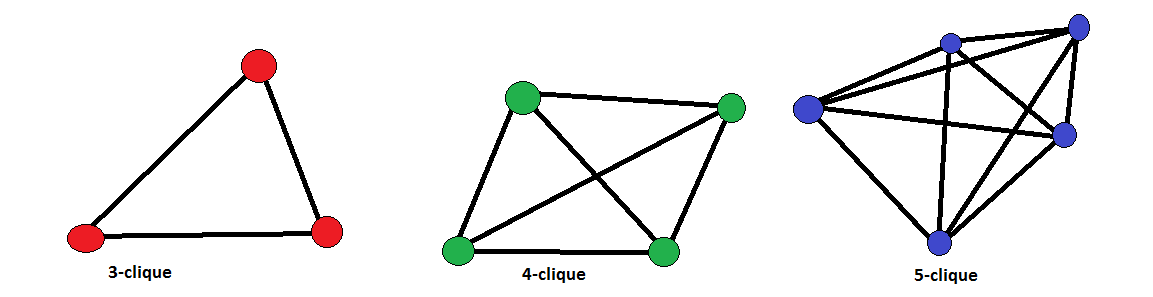

k-stable set

In a graph a $k$ - stable set is a collection of $k$ points such that no edges are present between these $k$ points are present. In the picture on the left cliques of size 3,4 and 5.

Well, if you think about this for quite some time it is remarkable what this statement says. It says that all possible graphs you can think of having a specific size either have a collection of $k$ points that are all connected to each other (a $k$ -clique), or a collection of $k$ points with no edges between any of these points (a k-stable set). 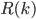A small painful detail missing from my argument is whether the Ramsey number $R(k)$ is actually a finite number, because the answer could simply be “Such a number does not exist!”, this would mean that no matter how large the graph gets it will not have neither a k-clique nor a k-independent set! Think what this means in the context of a party. Thankfully these numbers do exist! This result follows from a result Frank Ramsey proved himself in 1930.

Third occurrence

Coming closer to today, last week when I returned home I saw that the December issue of Nieuw Archief of Wiskunde had arrived. Whenever I receive a new issue I always open it to check all the articles. On page 232 I saw an article with title “Parties a smidgen smaller” written by Ross J. Kang. This article is dedicated “in admiration of the life and achievements of mathematician Ron Graham (1935-2020)”. In this article, Ross Kang recollects his time in Hungary visiting Ron Graham in 2006, the year the last major breakthrough concerning Ramsey numbers was set.

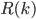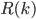Ow, something I forgot to mention, there is a very big issue with Ramsey numbers, they are extremely difficult to compute! Ramsey may have proven that his number $R(k)$ is, for every $k$ , finite but what $R(k)$ exactly is, is up to today a huge riddle. We have seen that 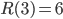$R(3) = 6$ and it is also known that 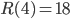$R(4) = 18$ (shown in 1969) but is still unknown what 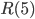$R(5)$ exactly is. The only result we have managed to obtain is that 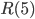$R(5)$ is greater than 43 and less than 48. On Wikipedia there is a famous quote of Paul Erdős showing the complexity of computing Ramsey numbers,

Erdős asks us to imagine an alien force, vastly more powerful than us, landing on Earth and demanding the value of 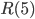$R(5)$ or they will destroy our planet. In that case, he claims, we should marshal all our computers and all our mathematicians and attempt to find the value. But suppose, instead, that they ask for 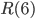$R(6)$ . In that case, he believes, we should attempt to destroy the aliens.— Joel Spencer

There is actually a result derived using computers that states that 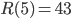$R(5) = 43$ .

Fourth occurrence

As a said in the beginning, recently there has been a major breakthrough in computing Ramsey numbers, not in the sense that a specific number has been computed but that an improvement has been found on how large these numbers can get as the number k gets larger. This new result comes fourteen years after the last breakthrough in this direction, from a young mathematician who just finished his bachelor studies at MIT, his name is Ashwin Sah! And his name is all around the news, making occurrences with Ramsey numbers a daily event!

In the end when a big step is made is some direction the information will reach you in some way or another!

Would you like to stay up to date when a new post appears on the Network Pages?

Subscribe to our mailing list