On a quiet afternoon, professor Meth is working in her office in Leiden on some tantalizing mathematics problems. Suddenly, someone knocking on her door nervously disrupts the silence.
X (nearly out of breath): Good evening, Meth. I apologize for not making an appointment beforehand. Still, I hope there’s some space on your agenda for a quick meeting. There’s a pressing matter that needs your urgent attention.
Meth (sitting calmly on her chair, with a rather large cup of coffee in her hand): I do not have an agenda, X. I go with the flow. What brings you to my compact little office? Oh, did you know that Fréchet, a French mathematician, originally coined the term “compact space” in 1904 to refer to a space where every sequence could not essentially ‘escape’? I sometimes feel I, too, cannot escape this office.
X (grabbing a bean bag to sit on): Fascinating, Meth, but I need your help. Today during my lecture, a student showed up intoxicated and, halfway through the class, decided to perform karaoke on…what was the name of the song, “Baby”, I suppose? By this person called Bieber.
Meth: Oh, I did hear about that, and that the student was, with high probability, intoxicated on Russian vodka.
X: What?! How did you know?
Meth: Just an educated guess. Students love vodka.
X: Not the vodka, Meth. How did you know about the incident?
Meth: Gossip, X. You know, you can think of all of us in a community as a network or a graph. Basically, as points connected with links, or as I prefer to call it, vertices connected with edges. And then, you can think of gossip as a disease spreading on this network.
X: Gossip as a disease? That is an interesting analogy…No, wait, Meth, that is not the issue at hand. As I was saying, this student decided to perform karaoke and then ran away from the lecture hall and is now somewhere in Amsterdam. How do I find them?
Meth (now turning to her laptop and working on the side): Gossip indeed can be thought of as a disease. It is essentially a process on a network. An excellent way to study this is using what we call spectral theory.
X: Meth, we have a missing student.
Meth: Oh right, of course. Well, spectral theory to the rescue again.
Meth: Ah, so you do not. Take this rubber sheet, X. You can see that I have drawn a circle on it, with some lines inside it. What are all the possible things you can do to this sheet so that the lines remain lines and do not get deformed?
X: I certainly cannot fold it. Why are we doing this?
Meth: To understand eigenvalues, of course! So, what can you do then?
X: I can rotate it.
Meth: Excellent! Anything else?
X: I can also stretch it, I guess?
Meth: Fantastic! These are what we call linear transformations.
X: And this rubber sheet will find my student??
Meth: Bear with me, X. There are no easy answers in mathematics. So, back to linear transformations. You may notice that the circle gets deformed when you pull the sheet. The direction in which the circle deforms is an eigenvector of the transformation. The factor by which it scales is the eigenvalue. So, suppose you place the sheet over the map of Leiden and stretch it towards Amsterdam. In that case, your eigenvector is essentially a vector in the direction from Leiden to Amsterdam. If you stretch it enough to double the radius, your eigenvalue equals 2. The takeaway from this fun exercise is that an eigenvector is a direction along which a particular transformation acts only like a stretch/compression or rotation. The eigenvalue tells you about the factor by which this occurs.
X: Okay, now this eigenvalue tells you where my student is?
Meth: Not directly, of course.
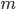X: We are wasting time, X. Meth: Trust the process, X. Let me now tell you what a matrix is. A matrix of some size by (written as 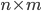) is a block of numbers. Each matrix entry is 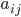where and 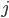range from 1 to and 1 to 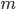. Thus, the matrix is 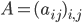. Still a little confused? Maybe this image might help!
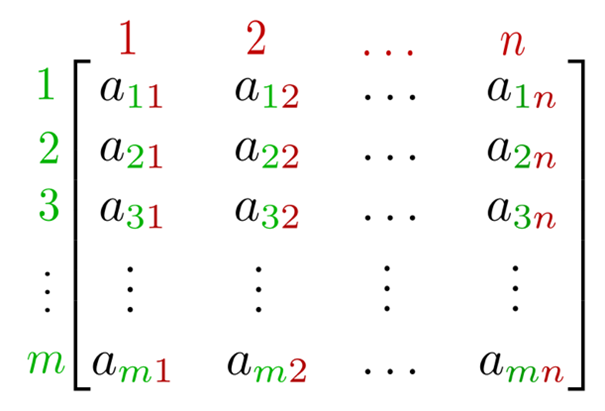
The central focus of the field of linear algebra is to study the eigenvalues of these matrices.
Curious about the word ‘linear’? Well, every matrix is a linear transformation!
X: So a matrix is a linear transformation? And thus you can find its eigen…something?
Meth: You are brilliant, X. Yes, you can find its eigenvalues and eigenvectors. Now, I had mentioned networks previously, correct? You can now think of Amsterdam as a network, with each junction connected by roads. The roads are the edges or the links, and the junctions are the vertices or the points. Please do not ask me how I know this, but I can certainly tell you that a vodka-induced walk is a random walk. So your student is essentially performing a random walk on a graph; at each junction, they change their direction randomly.
X: What does any of that have to do with eigenvalues and matrices?
Meth: Here comes the fun part, X! You can think of every network as a matrix! If you label all graph vertices as numbers from 1 to n, assuming there are n vertices, you can make an 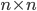size matrix. It does not matter how you label your vertices, as long as each is labelled distinctly. You can even label them with the Greek alphabet, though that might be slightly messy. If an edge or a connection exists between a vertex 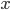and a vertex 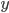, then the entries 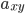and 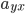are 1, and if there is no edge, these entries are 0. We call this an adjacency matrix. You can now find its eigenvalues.
X: Okay, suppose I magically do get these eigenvalues. How does it find my missing student, Meth?
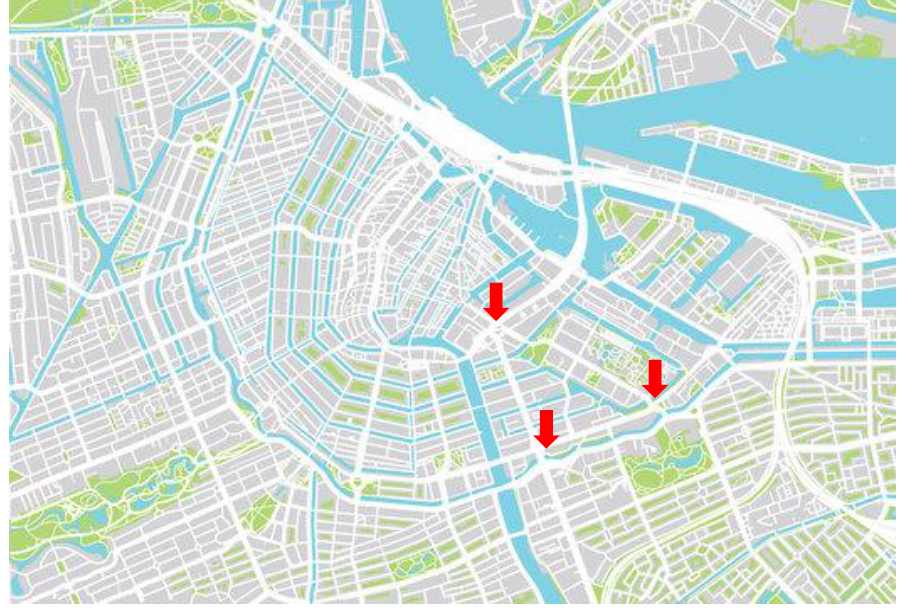
Meth (handing over a sheet of paper to X): Here is a list of three places in Amsterdam that are extremely well connected to the rest of the city, that is, they are vertices with high degree. Could you ask someone to get the places checked? Perhaps within a small epsilon-neighborhood.
X: These?? Are you sure? It seems a bit unlikely a student would end up here. And a what neighbourhood?
Meth: A sober student, perhaps.
…
(a while later)
…
X: I just received this text that says the student was found near one of the places you had listed. How did you figure this out?
Meth (finally closing laptop): You see, you will get a bunch of eigenvalues for a network. The difference between the largest two is what we call a spectral gap, which gives you information or control on what we call mixing time for a random walk on your network.
X: A mixing what?
Meth: Mixing time, X. Picture a student wandering randomly in the streets of Amsterdam after a day of exhaustive… sorry, interesting lectures. The student could start anywhere on the network, given by an initial distribution. The mixing time is the time after which the chance of the student being on any vertex of the graph or network is proportional to how connected that vertex is, that is, more connected vertices have a higher probability. Based on my estimates, during the time I was giving you a crash course on spectral theory, your student’s vodka-induced walk had very likely achieved its’ mixing time.
X: That does seem intuitive now that I think about it.
Meth: Now that you’re here, how about I reveal to you the gossip part over a coffee?
X: A coffee would be lovely, Meth.
Meth: You see, one can model epidemic spread on networks. If you’d like to know more about that, you will have to talk to my colleagues. But I can tell you one interesting thing from a spectral theory perspective. Every epidemic has an epidemic threshold. When specific parameters of your model are below this threshold, the epidemic will die out. If it exceeds that value, we will observe an outbreak.
X: You haven’t mentioned anything about an eigenvalue yet, but I feel it’s hidden in there somewhere.
Meth: It is. The epidemic threshold is closely linked to the largest eigenvalue of the graph. I won’t go into the technicalities, but I just wanted to share with you how these spectral properties of networks can help you understand many exciting things about real-world phenomena having an underlying network structure.
X: Why don’t you all do this more often for real-world networks and tell us the answers?
Meth: Oh, real-world networks are very complex. You can model them with something called random graphs.
X: Random graphs?
Meth: Forget what I said. The honest answer is funding, X. We need more funds and not-so-compact offices. Oh, did I tell you about Fréchet and compact spaces?
This line of research in NETWORKS is funded by the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant no. 945045.
Imagine you’re in a remote village and only have a limited number of vaccines to distribute to protect the community from a deadly virus, who do you vaccinate?
A difficult decision, but necessary. Assuming that the disease is just as deadly for everyone in the community, the best way to prevent deaths is to contain the spread of the virus.
How is it possible that bikes are so perfectly spread out that they are available from almost anywhere? Who are these bike fairies that distribute them evenly across the city? Continue reading if you like to find out who they are and what type of mathematics is involved.
Percolation theory is a branch of mathematics at the interface between probability theory and graph theory. The term 'percolation' originates from materials science. A representative question is as follows. Suppose some liquid is poured over a porous material. Will the liquid be able to make its way from hole to hole and reach the bottom?
by 
(written as 
) is a block of numbers. Each matrix entry is 
where 
and 
range from 1 to 
. Still a little confused? Maybe this image might help! 
size matrix. It does not matter how you label your vertices, as long as each is labelled distinctly. You can even label them with the Greek alphabet, though that might be slightly messy. If an edge or a connection exists between a vertex 
and a vertex 
, then the entries 
and 
are 1, and if there is no edge, these entries are 0. We call this an adjacency matrix. You can now find its eigenvalues. 
