New breakthrough about Ramsey numbers?
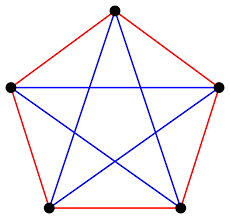
In a seminar talk in Cambridge this week, Julian Sahasrabudhe announced that he, together with his colleagues Marcelo Campos, Simon Griffiths and Rob Morris, had obtained an exponential improvement to the upper bound for Ramsey's theorem.
Playing with Colors Part 2: An open problem related to graph colouring
Mathematicians often enjoy playing around with the concept of infinity and in the following, I will describe a problem defined on an infinite graph!
Playing with Colors
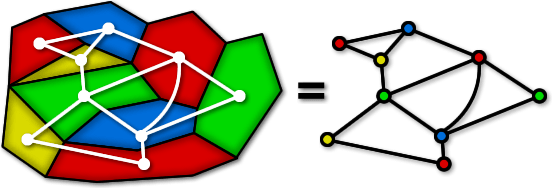
Part 1: Learn about applied and theoretical aspects of graph coloring: a tool that helps us design exam schedules or even solve Sudoku!
Let me tell you a story from my teaching
On Wednesday I was teaching an exercise class on graph theory. There was this one exercise that was troubling me for a couple of days, I couldn't solve it and it was frustrating.
Start to jet lag behind. Moving to fairer competitions.
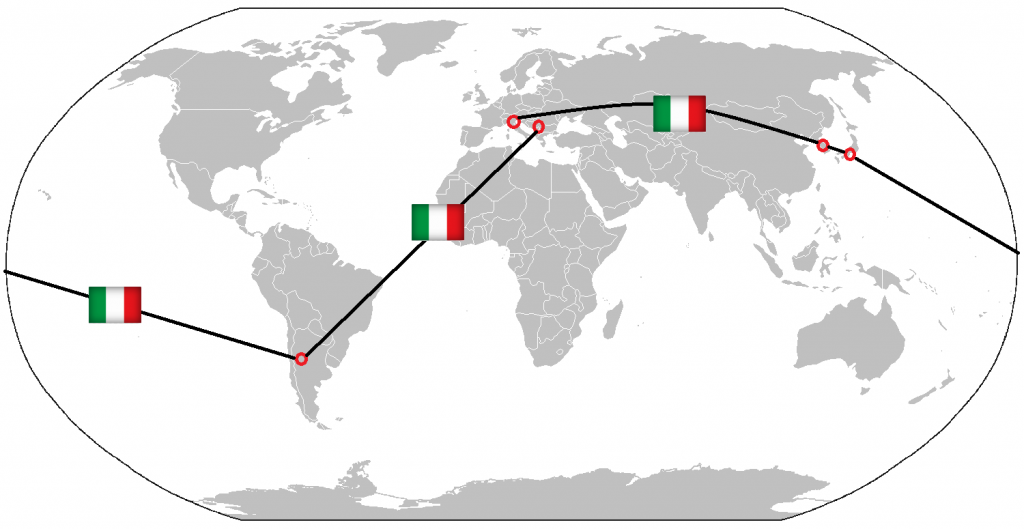
It is safe to say that traveling impacts the peak performance of teams and athletes in general - studies have been done across all kinds of sports that confirm this intuitive idea. Thus, to avoid unfair- and unhappiness, an organizer should aim to minimize the effect of travel time disparities.
From Tweets to Communication Networks
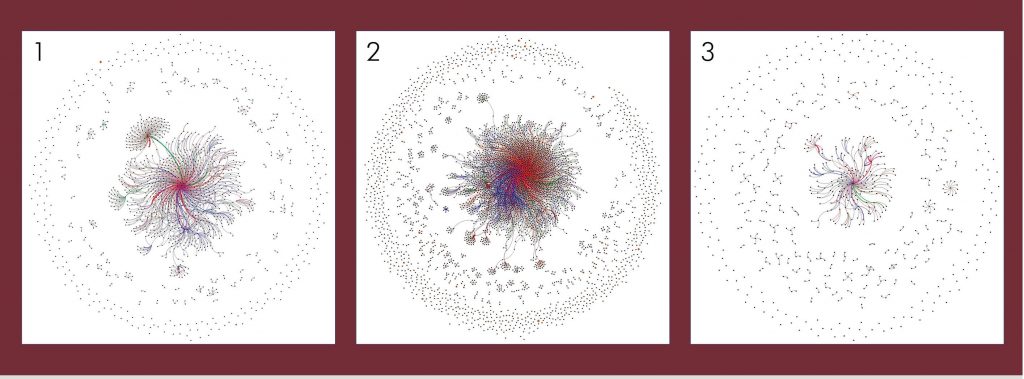
Network visualizations have the power to display how we communicate with each other in social media. We can simply depict message exchanges using communication networks. In such a network, nodes represent users, and there exists an edge between two nodes when the corresponding users exchange information (an email or a tweet).
Eigenvalues to the rescue
On a quiet afternoon, professor Meth is working in her office in Leiden on some tantalizing mathematics problems. Suddenly, someone knocking on her door nervously disrupts the silence.
What have Donald Trump, an epidemiologist and a rock in common?
In this article, dear reader, I am going to show you in which way the development of your opinion during the last political issue, the spread of a virus among your acquaintances during the current pandemic, and the alignment of some particles lying inside the device from which you are reading this article are extremely comparable phenomena.
The travelling salesman problem
Suppose you have a delivery service. You have one truck and have to deliver a large number of parcels to different cities in the country every day. Then you run into the following problem: in which order should you visit the cities?
How do you decide who is the most important?
Imagine you’re in a remote village and only have a limited number of vaccines to distribute to protect the community from a deadly virus, who do you vaccinate?
A difficult decision, but necessary. Assuming that the disease is just as deadly for everyone in the community, the best way to prevent deaths is to contain the spread of the virus.