Playing with Colors Part 2: An open problem related to graph colouring

In Part 1 of this series on graph coloring, all the graphs that we saw were finite, i.e., they had a finite number of edges and vertices. This of course makes sense since they were derived from real-world applications. Mathematicians often though enjoy playing around with the concept of infinity and in the following, I will describe a problem defined on an infinite graph.

In this graph, which I will denote with 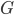$G$ , the set of vertices corresponds to all the points of the two-dimensional plane. Two vertices in 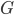$G$ are connected by an edge, whenever the two corresponding points have distance exactly equal to 1. This graph is called the unit distance graph of the plane.

Now the problem is:

What is the chromatic number of 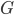$G$ ?

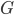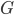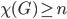Of course, it is hard to really imagine how this graph looks like since it has an infinite number of vertices and edges. But, what we could do to attack the problem is look at finite parts of $G$ . If we can show that there are finite parts of $G$ that necessarily need at least $n$ colours, then it has to be true that $\chi(G)\geq n$ .

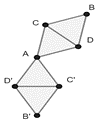
We construct a graph 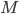$M$ with the following steps: we start with two identical rhombi 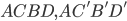$ACBD, AC'B'D'$ whose sides have length equal to 1. Then, by known properties, we also have that 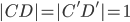$|CD|=|C'D'|=1$ . Now we will rotate the rhombus 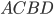$ACBD$ clockwise around point 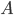$A$ . Clearly, during this rotation 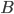$B$ comes closer and closer to 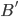$B'$ so at some point we will have 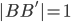$|BB'|=1$ . At that point, we stop rotating. The resulting graph is seen in the right picture below and is called the Moser Spindle. Since any two connected vertices in this graph have a distance 1, we know that 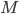$M$ is a subpart of 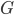$G$ , or as we say in graph theory, 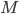$M$ is a subgraph of $G$ .

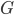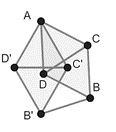
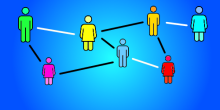
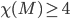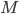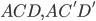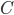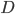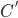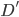It’s not hard to see that $\chi(M)\geq4$ : assume that you could color $M$ with three colors, let’s say blue, green, and red. Without loss of generality, assume that point $A$ has the color blue. Clearly, because of the triangles $ACD, AC'D'$ , vertices $C$ and $D$ must use green and red (and the same holds for $C'$ and $D'$ ). 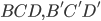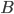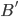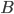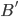But then, due to the triangles $BCD, B'C'D'$ only the color blue is left for both $B$ and $B'$ which is not allowed since $B$ and $B'$ are connected. The above argument is illustrated in the picture below.

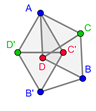
This in turn implies that 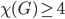$\chi(G)\geq4$ . This is what we call a lower bound for the chromatic number of the unit distance graph of the plane. Now we would like to also derive an upper bound, i.e., prove that 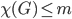$\chi(G)\leq m$ for some integer 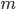$m$ . To do that we will actually show how to color 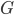$G$ with 7 colors. The idea for this is simple but elegant.

Regular tilings of the plane

A regular tiling of the plane is a way to cover the plane with copies of the same regular polygon. Below you see the three possible regular tilings of the plane: with regular triangles, squares, or hexagons. For our purposes, we will use the tiling with hexagons.

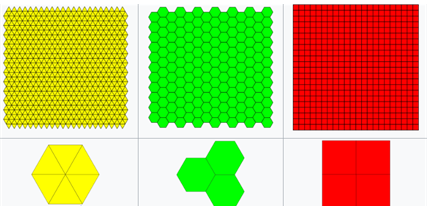
Namely, we consider a regular tiling of the plane with hexagons that have diameter slightly less than 1. In turn, this means that any two points in the same hexagon have distance less than 1, which means that they would never be connected in 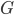$G$ . So, all the points within one hexagon can use the same color. But still, how many different colors do we need? The following picture speaks for itself:

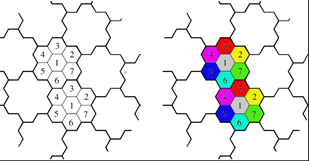
Namely, we see that if we use 7 colors as in the picture, any two hexagons of the same color, are sufficiently far away. Subsequently, any two points at distance exactly one will lie in hexagons of different color. Hence we have shown that 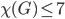$\chi(G)\leq 7$ . How many colors would you need if you would use squares or triangles instead of hexagons?

A recent breakthrough

In 2018, the famous biologist and computer scientist Aubrey de Grey using a rather involved construction that required computer assistance, generated a unit-distance graph that is not 4-colorable, hence showing that 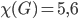$\chi(G)= 5, 6$ or 7. His idea was to combine many copies of the Moser Spindle we saw earlier in a very large graph. His initial monstrous construction had 20,425 vertices which he managed to bring down to 1,581 vertices. At this moment, the smallest example of a unit-distance graph that is not 4-colorable has 509 vertices. One could imagine that through some more involved, and probably larger, construction, a unit-distance graph that is not 5-colorable could be generated by a computer. Perhaps the interested reader could attempt to construct such a graph.