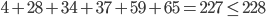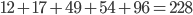An introduction into complex problems.

Are you one of those people who always seems to pack just a bit too much for your car to handle when packing for a vacation? Then you’re probably familiar with the packing-your-car-Tetris game: given a number of items and bags, can you fit all of these in the back of your car? Some will argue that this is a fun game, for other this might be a straight-up nightmare. However: most will agree, this can be a pretty hard game to win. In this article, I will introduce you to the magical world of computational complexity and will let you feel what makes packing your car generally hard.
So why is packing your suitcases into the car so complex? Obviously, it is a 3-dimensional packing problem: we want to pack certain 3D items called suitcases into a 3D space called the trunk. I claim that this is even hard in 2 dimensions. For example, take the puzzle of Steward Coffin on the right with only five(!) pieces which need to be placed into a square tray. You can see these pieces as 2-dimensional suitcases that need to fit into a 2D space, namely the square.

Even if the pieces are just rectangles, for example in the figure on the left, this is an extremely hard problem. You can try this for yourself here!
If it is already hard to do this in two dimensions, I hope you agree three dimensions is even harder.
The Arithmeum museum in Bonn has an exposition on Chip Design, which can be partly viewed on their website. If you go to here and choose Placement and then Game you can play a 2D packing game with rectangles, which is part of this exposition. I would encourage you to start with only a few items and after each success increase the number of items to pack by two. Hopefully you’ll notice it will get a lot harder with each extra item!
Bin Packing
When we play this game in only 1 dimension, we call it `bin packing’. In this case, we are given so-called bins with a certain capacity and items of a length that need to be distributed over these bins. This type of problem occurs for example when you are packing several suitcases for flying, where each suitcase can weigh at most 23kg. In business, this problem appears when distributing tasks (the items) over the workday of employees (which can be seen as the bins).

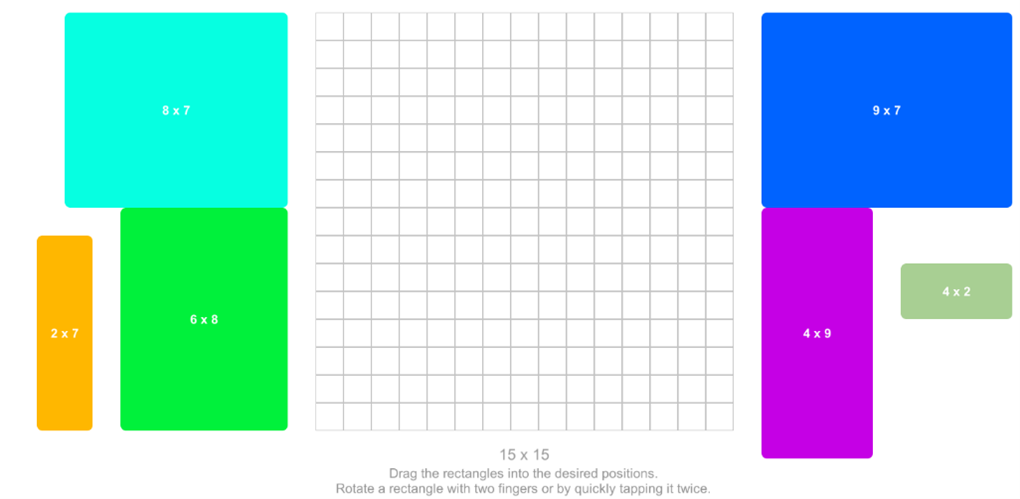
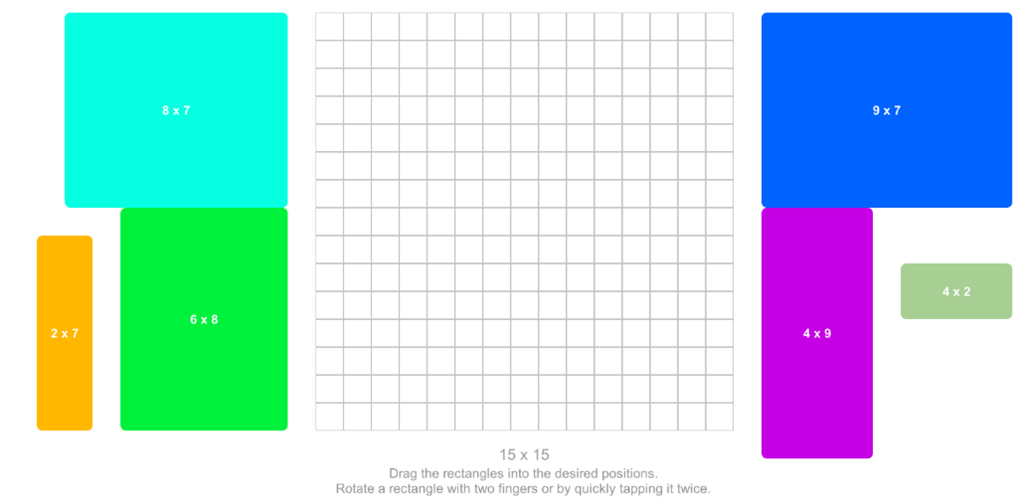
Even though Bin Packing is a problem played in one dimension, it remains hard to solve. Let us first look at a simple example, say that I have 6 items of lengths: 8, 7, 7, 5, 2, and 1, can we fit it into two `bins’ of length 15? Try to solve this in the interactive game below, you can move the items with your cursor.
Probably, you can solve this in a couple of seconds, either by just trying or by remarking that 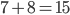 and that
and that 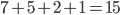 , so indeed this would fit.
, so indeed this would fit.
In the following game you can try it yourself. You can choose the number of bins you want, and you have to put the items in them so that they can fit precisely.
However, what if I give you the following set of lengths of items: {4, 12, 17, 28, 34, 37, 49, 54, 59, 65, 96} and I want to distribute them over two bins of capacity 228? Can you do that? How much harder did the problem get, even though the number of items only doubled?
Can’t we just use computers?
Well yes—and no. Of course we can use computers for this, however, a computer needs a set of instructions to follow, also called an algorithm. In other words, we need a structured way to find a solution. An example of an algorithm for Bin Packing with two bins could be:
For all combinations of items  :
:
- compute whether all of
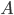 fits into one bin, and
fits into one bin, and - compute whether all items not in
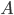 fit into one bin.
fit into one bin.
If both are yes: we found a way to distribute the items.
If the answer is no for each combination of items 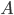 , there is no way to distribute these items.
, there is no way to distribute these items.
In the example of 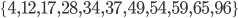 and two bins of capacity 228, the algorithm will find the solution when it chooses
and two bins of capacity 228, the algorithm will find the solution when it chooses 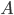 as {4, 28, 34, 37, 59, 65}.
as {4, 28, 34, 37, 59, 65}.
So, we can use a computer to solve Bin Packing. How long will the computer take to compute this?
This obviously depends on which computer you use and how fast it is: The computers that are produced today are many times faster than those that run on Windows XP from 2001. However, we can say something about the number of computations the algorithm (and therefore the computer) takes. The algorithms above will do two computations (namely a. and b.) per combination of items. So how many combinations of items are there?
Well, if  is the number of items, then each item can be either a part of, or not a part of any combination. This gives us a total of
is the number of items, then each item can be either a part of, or not a part of any combination. This gives us a total of 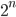 different combinations to check. Hence, the number of computations scales exponentially in the number of items. If you recall exponential growth from corona, then you’re probably aware that this is not a good thing. Because of this
different combinations to check. Hence, the number of computations scales exponentially in the number of items. If you recall exponential growth from corona, then you’re probably aware that this is not a good thing. Because of this 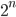 combinations we check, the number of combinations doubles if we add one item to the problem (see also the table on the right). So, if my computer takes 1 second to do Bin Packing with 10 items, it will take for Bin Packing with 20 items around
combinations we check, the number of combinations doubles if we add one item to the problem (see also the table on the right). So, if my computer takes 1 second to do Bin Packing with 10 items, it will take for Bin Packing with 20 items around 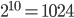 seconds which is around 17 minutes. And if you want to compute this for 50 items, well…. It would take about 35.678.376 years. I don’t think we would have time to wait for that. So yes, we are able to compute it using computers, but only up to a small number of items.
seconds which is around 17 minutes. And if you want to compute this for 50 items, well…. It would take about 35.678.376 years. I don’t think we would have time to wait for that. So yes, we are able to compute it using computers, but only up to a small number of items.
 | 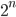 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 10 | 1.024 |
| 11 | 2.048 |
| 12 | 4.096 |
| 13 | 8.192 |
| 14 | 16.384 |
| 15 | 32.768 |
| 16 | 65.536 |
| 17 | 131.072 |
| 18 | 262.144 |
| 19 | 524.288 |
| 20 | 1.048.576 |
Can we do something smarter?
Well- not really! Or at least: not that we know of. Of course, the fact that we do not know of an efficient algorithm, does not necessarily prove that it does not exist.
For two bins, the best algorithms need about 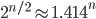 computations. For three bins, the best algorithms need about
computations. For three bins, the best algorithms need about 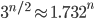 computations. For any other number of bins, there was a recent breakthrough by my co-authors and me, where we present an algorithm that needs about
computations. For any other number of bins, there was a recent breakthrough by my co-authors and me, where we present an algorithm that needs about 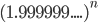 computations.
computations.
However, the computer science community believes that efficient algorithms (those that only need for example around 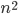 or
or 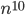 computations) do not exist for Bin Packing. This belief is based on a hypothesis referred to as “
computations) do not exist for Bin Packing. This belief is based on a hypothesis referred to as “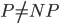 ”; If you would be able to design an efficient algorithm for Bin Packing it would show that
”; If you would be able to design an efficient algorithm for Bin Packing it would show that 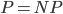 . Why does that matter?
. Why does that matter?
Well first of all, you would earn a million dollars, as showing 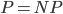 is one of the millennium price problems. In theory, which would be nice. However, it would also imply that we can solve many other problems efficiently. That may sound wonderful in theory, until you realize that our security systems are then suddenly also easy to crack! So, giving an efficient algorithm for Bin Packing would actually have a lot of impact on our society.
is one of the millennium price problems. In theory, which would be nice. However, it would also imply that we can solve many other problems efficiently. That may sound wonderful in theory, until you realize that our security systems are then suddenly also easy to crack! So, giving an efficient algorithm for Bin Packing would actually have a lot of impact on our society.
Is that only true for Bin Packing?
No! There are actually many, many so-called 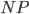 -hard problems such as Bin Packing. Giving an efficient algorithm for any of these NP-hard problems would also show
-hard problems such as Bin Packing. Giving an efficient algorithm for any of these NP-hard problems would also show 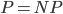 and therefore have the same impact. These are often fun games to solve with many applications. Let me give you some examples of such
and therefore have the same impact. These are often fun games to solve with many applications. Let me give you some examples of such 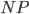 -hard problems.
-hard problems.
Steiner Tree: In this problem, you’re given points that need to be connected with using as few connecting lines as possible. You can play this game here and then clicking ‘Routing’. The website explains one of the applications of this problem: connecting parts of a chip while using the least amount of connecting fluids.
Travelling Salesman Problem: In this problem, you want to find the fastest route visiting a set of cities. You can play this game here. You can encounter this problem for example when a Picnic or PostNL car has to visit a set of customers.
3-coloring: In this problem, you’re given a set of points and lines between the points. You need to color the points red, blue or green, such that for each line, the endpoints receive different colors.
So what should I do with my car?
There is actually some good news: not all packing problems are hard! Sometimes the solution is actually relatively easy to find, and we humans seem to be remarkably good at finding these types of structures. So: maybe you’re lucky and with a bit of hard Tetris work, you can manage to pack your car. But if you can’t, there is actually a really easy solution:
Just pack a bit less next time.
Thanks for reading this article about complexity theory. If you’re searching for a subject for a school project or a 'profielwerkstuk’ related to computer science or mathematics, I can recommend studying any of the problems above, matching problems, or for example puzzles like Sudoku. Understanding (the complexity of) the problem, being able to implement/compare some of the algorithms for it, and looking for applications for the problem can all be part of the project.