The routes that pickers in warehouses take are essential to efficiency. But which route is best?
You come home late in the evening and start cooking your dinner, but to your surprise, you miss the most important ingredient of the recipe. Luckily, nowadays you can order groceries on your phone at the click of a button. Within minutes the groceries are delivered to your doorstep. But how do these companies actually deliver these groceries this fast? How can they ensure that the food is delivered within 10 minutes? To answer these questions we need to take a look at their warehouses.
Gorillas and Flink are two well-known fast-grocery-delivery services in the Netherlands. Both companies make use of a spread of warehouses throughout their regions to maintain short delivery times. So, when your order is delivered too late, you know that the picking process was the cause.
The picking of orders in warehouses is not much different from getting your groceries from the supermarket. You need a collection of items located throughout the building (warehouse or supermarket) and you walk to each item, pick them up, and then leave.
Warehouses, just like supermarkets, consist of a collection of aisles with horizontal aisles at both ends, also called cross-aisles. The cross-aisles allow the picker to move from one aisle to another, and can also be placed in the middle of an aisle. Warehouses without such a cross-aisle are called single-block, while those with cross-aisles are multi-block.
When walking into a grocery service warehouse, you would be surprised at how they look incredibly similar to supermarkets but also surprisingly different. The items are stocked similarly and the layout even looks the same. But, the products are no longer grouped by type, instead similar products lay further away from one another. It is more difficult for pickers to see the difference between products that look the same. How quickly can you differentiate between kidney beans and chili beans or garlic and onion powder?
The warehouses of these companies thus take several precautions to prevent long picking times. Nevertheless, the routing of pickers is the most crucial part of warehouse's efficiency, as walking time makes up the largest fraction of the picking time.
How would you walk through a warehouse? Play the game below and try to find the shortest route. You can play the game by clicking the I/O point and dragging your mouse along the aisles. Once you have finished your picking process, you can click the I/O point again to finish the route. You can also use the buttons above to try again, set a new order, or see the optimal route and the so-called S-shaped route.
Shortest routes may not be optimal
As you can see the shortest route is quite hard to find, especially in multi-block warehouses! And since each order has different pickup locations, this route can change significantly every time. You can imagine that taking the shortest route, over and over again for different orders, can be quite confusing, as there is no intuition to it. Especially, considering that the warehouse employees don’t see the warehouse from above.
We thus need a smarter way to walk through the warehouse, one that does not confuse the pickers but one that still is sufficiently efficient. For this, we can use the method that most supermarket visitors deploy, the so-called S-shaped routing policy.
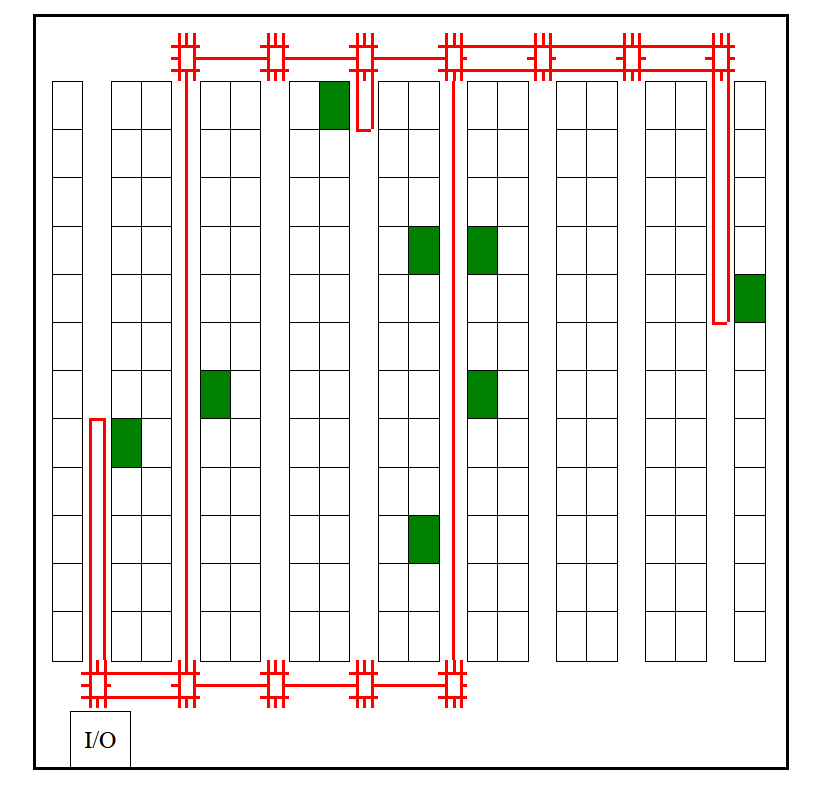
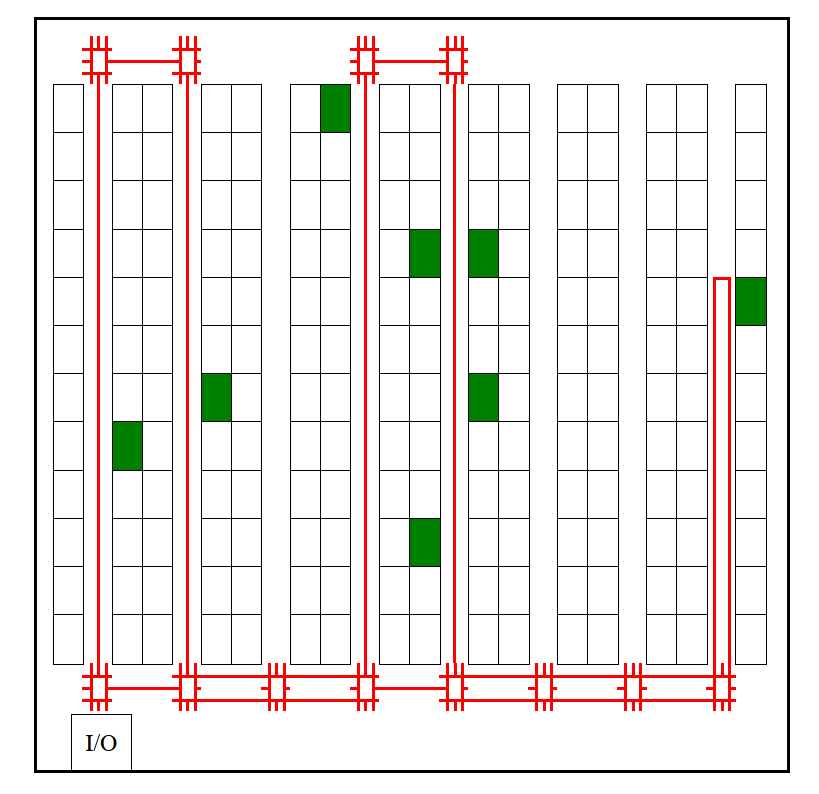
Always looking for the shortest route (left route) can become confusing. This is why the S-route policy is prefered (right route).
Under this routing policy, you slither through the aisles like a snake, creating several S’s on its side. This implies that the picker walks through every aisle with picks completely and then returns to the input/output point. Click on the S-shaped route button in the puzzle above to see how this works.
But why do we need probability theory?
Each different order that is requested contains completely different items, so each different order needs a different route. A new order has different pick locations than the previous order. Look again at the puzzle above, try pressing new order to see how this changes and see how the routes change as well. Probability theory can now help in analyzing the efficiency of a warehouse. How long does a picker have to walk on average? How can we design our warehouse to make the routes shorter on average?
The pick locations are thus randomly located in the warehouse. The route length of each of these orders thus is different. So how can we still ensure some efficiency?
Consider a warehouse with aisles and no horizontal aisles. Assume that each pick in an order has a probability to be within an arbitrary aisle. So, when a new order, containing a single item, arrives in the warehouse, the probability that an item is requested in aisle 1 is given by .
When an order containing items arrives, this probability becomes . We can see this by rewriting the probabilities as follows:
The random process behind the appointment of picks to aisles is actually related to a classic problem in probability theory: the occupancy problem. In this problem, a person throws a fixed number of balls, , at urns. Each different throw has a probability to hit a specific urn. This classic problem, variants of which you might have seen in high school, answers questions like the expected number of urns that are hit or the probability that you hit exactly one urn.
In the order-picking setting, the items can be seen as the balls and the aisles as urns. Every time you throw a ball you reveal an item's location. So, instead of reinventing the wheel, we can use the theory of this seemingly unrelated problem to answer questions about the routes in warehouses. For instance, the expected number of urns that are hit by at least one ball, i.e. the expected number of aisles with at least one pick is given by:
\begin{equation*}
\text{Expected number of aisles with picks} =
E \left[ \sum_{i= 1} ^k 1_{\{\text{aisle } i \text{ contains a pick}\}}\right] = \\
\sum_{i=1}^k P(\text{aisle } i \text{ contains a pick}) = k - k (1-\frac{1}{k})^n .
\end{equation*}
Similarly, the furthest aisle, on average, with picks is the urn with the largest index that has been hit:
\begin{equation*}
P(\text{furthest aisle with less than } j \text{ picks}) = P( \text{ all picks in aisles } 1,\cdots j) \\
= \left(\frac{j}{k}\right)^n
\end{equation*}
Using this formula we find
\begin{equation*}
\text{Expected furthest aisle with picks} =\\
\sum_{i=1}^k \left(1- P(\text{furthest aisle with less than } j \text{ picks})\right) = \\
k -\left(\frac{1}{k}\right)^n - \left(\frac{2}{k}\right)^n - \cdots - \left(\frac{k-1}{k}\right)^n .
\end{equation*}
Playing around with this formula we see that if we have aisles and orders then on average the furthest aisles with an order are aisles 7, 8, and 9 respectively. For aisles and orders we have that on average the furthest aisles with an order are aisles 20, 23, 28, and 29 respectively. Play around with these formulas and see for yourself what conclusions you can draw about making a warehouse more efficient!
We thus see that a classic problem in probability theory allows us to analyze some crucial elements of the route that pickers take. Namely, the expected distance to the furthest aisle and the expected total number of aisles that have to be visited. Recall that under the S-shaped routing policy, the picker always travels through the entire aisle, so the total length of a route that the picker takes is the sum of the two elements discussed above.
Remark: The exact theory is a bit more involved. When an odd number of aisles has to be visited, the picker ends up on the wrong side of the warehouse, so an extra aisle needs to be visited.
We saw that the routing problem in warehouses has many layers to it, including the choices you make for the routes, but also the randomness in the pick locations for each different order. I showed you how we could apply probability theory to get some insights into the picking time, to see whether or not a routing policy was efficient enough. Hopefully, with this theory, the picker was fast enough to deliver your missing ingredient on time.
Did you know that if you divide a pack of cards into 13 piles of 4 cards, then you can always pick one card from each of the 13 piles so that there is exactly one card with each rank? There is some beautiful math behind this puzzle.
You have a job interview in 20 minutes and you are in a hurry to arrive at your application in time. To make matters even more stressful, there are many routes to your destination, but you have no idea which one to select. Luckily, you have access to a navigation system that can help you in your route selection process.
On Friday 24th of September Professor Ton Koonen received a royal distinction “Ridder in the Orde van de Nederlandse Leeuw” during the symposium “Optical Networks – communication fabric of our society”, preceding his valedictory lecture “Light work(s)”.
aisles and no horizontal aisles. Assume that each pick in an order has a probability 
to be within an arbitrary aisle. So, when a new order, containing a single item, arrives in the warehouse, the probability that an item is requested in aisle 1 is given by 
items arrives, this probability becomes 
. We can see this by rewriting the probabilities as follows:
aisles and 
orders then on average the furthest aisles with an order are aisles 7, 8, and 9 respectively. For 
aisles and 
orders we have that on average the furthest aisles with an order are aisles 20, 23, 28, and 29 respectively. Play around with these formulas and see for yourself what conclusions you can draw about making a warehouse more efficient!
