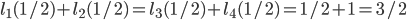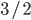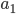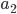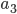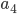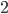Traffic congestion is a huge problem in urban areas nowadays, road networks are becoming rather complicated to design and extending the network is not always possible. But the, seemingly innocent and quite natural, idea to build more roads in order to solve the traffic problem can be sometimes quite a bad idea.
Of course when you build more roads you also give people incentives to use their cars more often because there is more infrastructure available. But that is not the only concern, adding an extra road, which may seem like a shortcut, will redistribute the traffic in the road network. Braess' paradox says that this redistribution of the traffic flow may lead to a larger average travel time! So building a new road may make the traffic problem even worse, especially when the road network is congested! This counter-intuitive phenomenon was first observed by Dietrich Braess in 1968 [1]. Similar paradoxal behavior has been observed also in other areas, like electrical grid networks and queueing systems [2]. In this article we give a detailed explanation and a mathematical description of the Braess paradox.
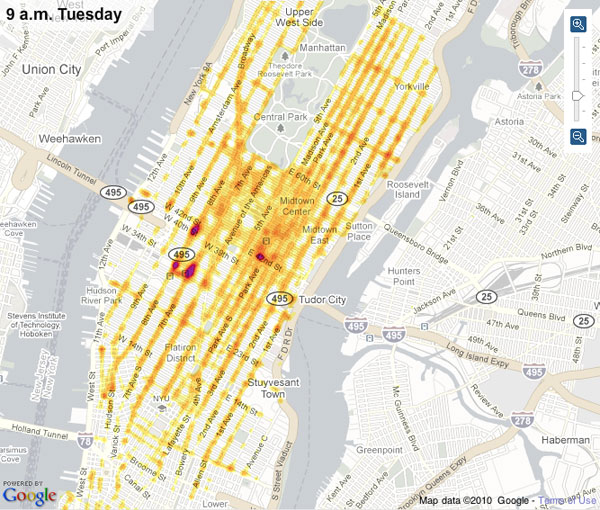
Before moving on to the mathematical analysis it is interesting to see some real-life cases where this paradoxal phenomenon has been observed! For example, there is a very nice article in the New York Times of December 25, 1990, describing a Braess paradox situation in New York City. On Earth day of that year, the traffic commissioner decided to close down 42nd Street, an always congested street. Quoting the commissioner Riccio: "Many predicted it would be doomsday". But, as it turned out, this prediction was completely false, the traffic situation actually improved when the street was closed down! Twenty years later, on February 2010, the mayor of New York decided to ban vehicles on Broadway from 47th to 42nd Streets and from 35th to 33rd Streets. The two main motivating reasons behind this action were improving traffic flow and pedestrian safety. In Figure 1 below we see the traffic times before and after the experiment, we observe that some streets get more congested while other streets get less congested. But on average the whole road network does not get much more congested than what it was before. The measurements and the figure were made by the New York City Department of Transportation.
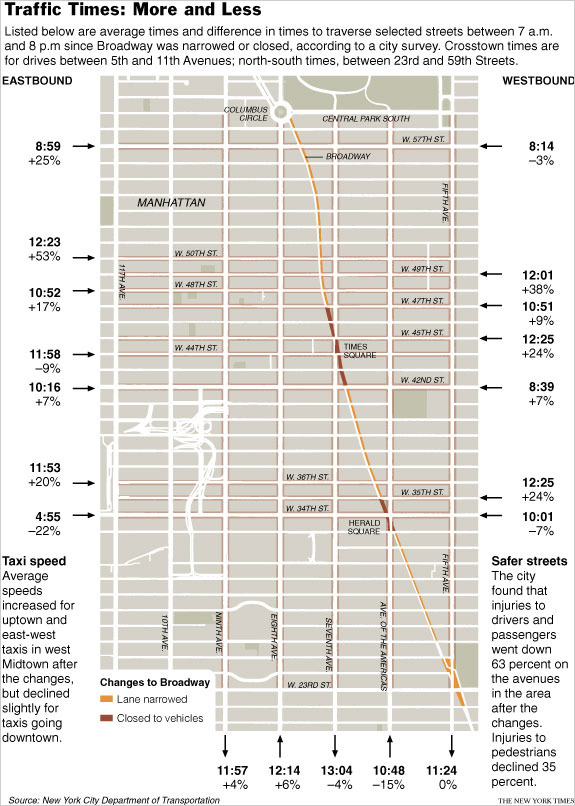
Figure 1: Traffic times before and after the experiment [5].
Mathematical explanation
In this section we give a mathematical description of the Braess paradox in the Wardop routing model [4] that we have also considered in the parts I, II and III of this series. This description of the Braess paradox, and generalizations of it, form an important role in a number of scientific papers for quantifying the inefficiency of traffic equilibria (of which we have seen an example in this article). Let us start by looking at the network below. As before, there is one unit of traffic flow that has to be routed from the origin 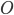to the destination 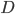. In the previous articles, we always considered the Pigou network consisting of two parallel roads. We now still have two parallel roads, but both roads consist of two parts (which is needed so that we can add an extra road section later). Remember that we use the functions 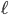to indicate the latency of a road section, which is the time needed to traverse it (and which can increase if the amount of traffic on the road section increases).
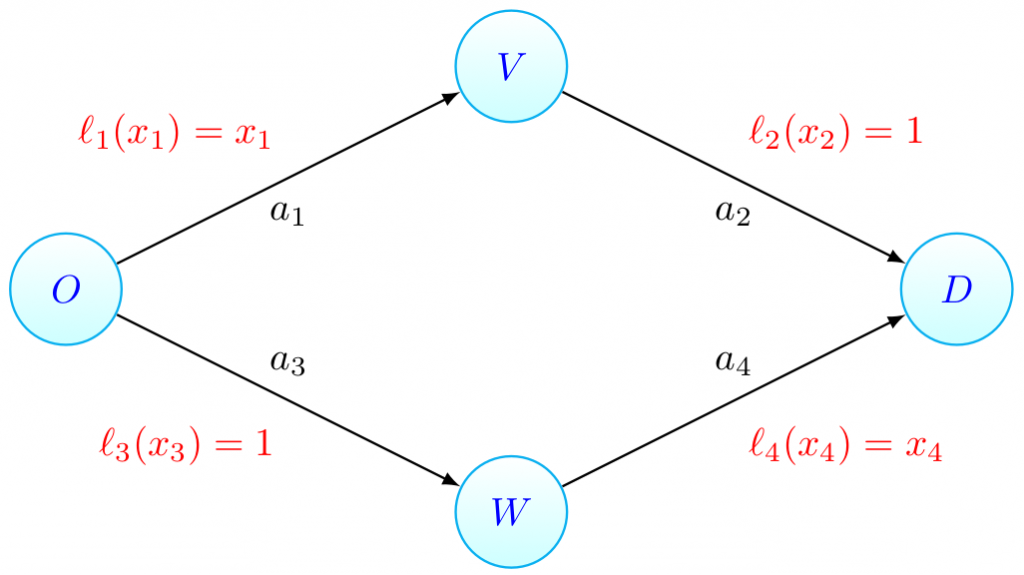
Exercise 5: What is the equilibrium flow in the network above? What is the average travel time?
Solution to Exercise 5: Notice that both roads have the same latency functions (but in a different order). Intuitively, you might suspect that the traffic splits up evenly among the upper and lower road. Indeed, if we set half of the flow on the upper road, and half of the flow on the lower road, then the latency of both roads is . Since the latency on both roads is the same, no fraction of flow can switch roads to get a better travel time, so this flow is indeed an equilibrium flow. The average travel time is .
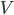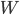We now add another road section to the network that connects the nodes and . This will be a very efficient road section, meaning that it takes almost no time to traverse it. In order to mimic the efficiency of the new road section, we give it a constant latency of 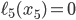. Note that we have created an extra road in the network, so the traffic flow can now even spread out over three roads leading from the origin to the destination. But, does this also happen?
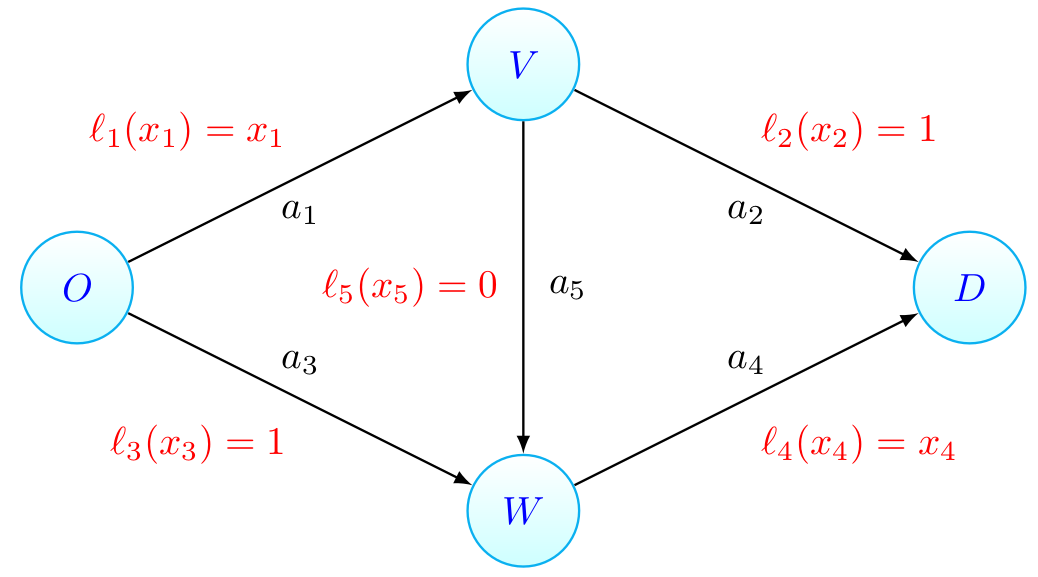
Exercise 6: What is the equilibrium flow in the network with the extra road section? What is the average travel time?
The new road section is very efficient, and therefore all drivers will want to use it. If all the flow is routed along the zig-zag road using the road section between and , then we find an equilibrium flow. To see this, note that the travel time of this road is . However, for both the upper road using section and , as well as the lower road using sections and the travel time is also (if all flow is routed along the zig-zag road), so no fraction of flow can improve by switching to the upper or lower road. The average travel time in the equilbrium flow is .
The exercises show that if we add a new road section, then the average travel time increases with 33%! Intuitively, this phenomenon can be described as follows. The introduction of the road section between 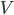and 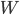gives drivers on both the upper and lower route the opportunity to improve their travel time by switching to the zig-zag path. However, as a result of this, the travel time on the upper and lower route goes up, leading to more drivers switching to the zig-zag path. But as a result of this, the travel time on the top and bottom path goes up even more. This process continues until all drivers have switched to the zig-zag path, on which the travel time has increased as well in the meantime. This is precisely the equilibrium flow we have seen in Exercise 6. Although switching to the zig-zag path is initially a good idea, this is no longer the case if everybody does this! Unfortunately, this will happen as a result of the drivers selfish behavior and wanting to minimize their own individual travel time.
The prevailing idea in the mathematics and engineering community is that when there is no traffic congestion in the network then adding new road segments will not have a negative effect on the average travel time. On the other hand, when there is traffic congestion on the network, adding a shortcut may lead to a larger average travel time! An important question that arises is the following, suppose we have a network with its latency values, are there edges in the network that have a negative effect on the average travel time when the network will be congested? This is an important question that experts need to take into account when designing a road network. The general problem is rather difficult to solve exactly, but there are algorithmic methods which can identify possible problematic edges. We refer to [3] for a nice overview and an analysis of this problem.
In the following animation, made by Bruno van Wayenburg, Braess' paradox is explained:
The Braess paradox shows that it is important to take into account selfish behavior of drivers when designing road networks. Extending a road network does not necessarily lead to a more efficient usage of the network.
References:
D. Braess (1968). Über ein Paradoxon aus der Verkehrsplanung.
J.E. Cohen, F. Kelly (1990). A paradox of congestion in a queueing network.
T. Roughgarden (2006). On the severity of Braess' Paradox: Designing networks for selfish users is hard.
J. G. Wardrop (1952). Some theoretical aspects of road traffic research.
The New York Times (2010). New York Traffic Experiment Gets Permanent Run.
Traffic jams are one of the biggest inconveniences in modern time. They lead to stressful situations for commuters, and cause huge economical and environmental damage. How could mathematics help?
In network congestion models, we make some simplifying assumptions that make our life easier. In a large-scale system, each individual driver contributes a tiny amount to congestion, if we assume that every car controls the same amount of traffic.
One way to mitigate the consequences of drivers' selfish behavior, is by introducing tolls (or taxes) on certain parts of the road network. This is also known as road pricing.
Congested road networks are a big problem in many countries. Building more roads is not always the best solution to solve this issue. One of the reasons for this is that drivers behave selfishly
Rapid urbanization without consideration for the environment is currently threatening urban dwellers. Its effects are exacerbating climate change and the urgency to adapt to our circumstances is growing. Network science may just have the key to solving our multifaceted problems.
to the destination 
. In the previous articles, we always considered the Pigou network consisting of two parallel roads. We now still have two parallel roads, but both roads consist of two parts (which is needed so that we can add an extra road section later). Remember that we use the functions 
to indicate the latency of a road section, which is the time needed to traverse it (and which can increase if the amount of traffic on the road section increases).
and 
. This will be a very efficient road section, meaning that it takes almost no time to traverse it. In order to mimic the efficiency of the new road section, we give it a constant latency of 
. Note that we have created an extra road in the network, so the traffic flow can now even spread out over three roads leading from the origin to the destination. But, does this also happen?
