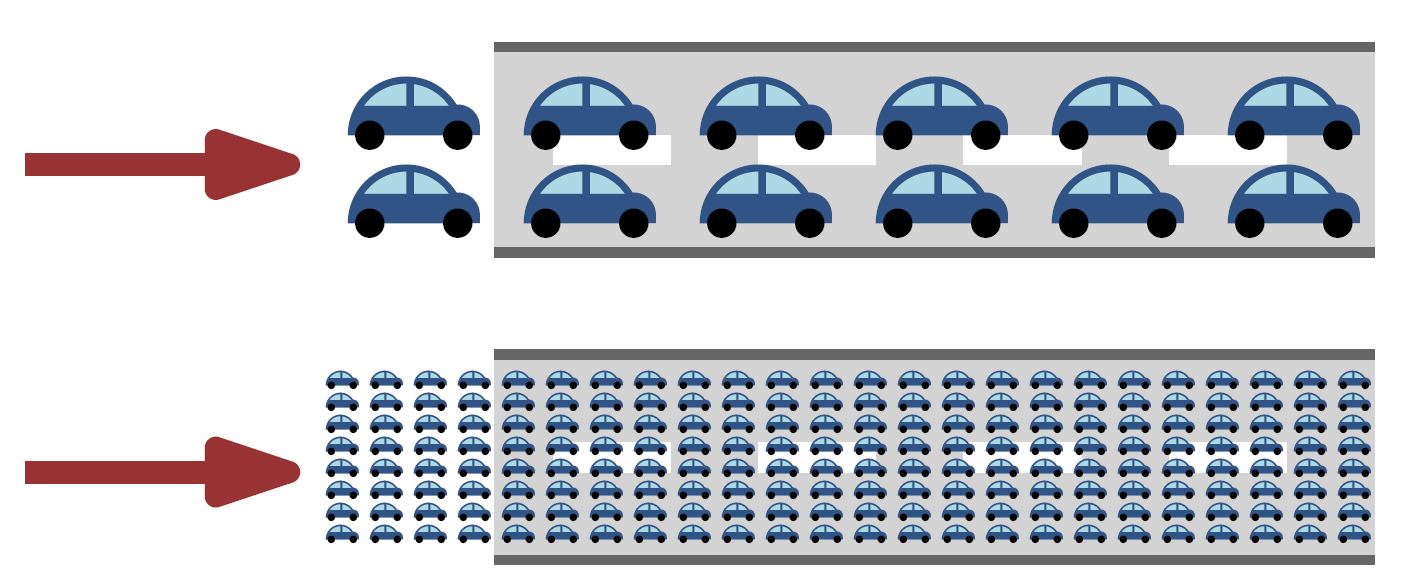
In network congestion models, we make some simplifying assumptions that make our life easier. In a large-scale system, each individual driver contributes a tiny amount to congestion, if we assume that every car controls the same amount of traffic.
That is, when we have 10 cars, we say that each one of them controls 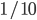 th of the traffic, or, if we have
th of the traffic, or, if we have 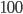 cars, then each one of them controls
cars, then each one of them controls 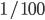 th of the traffic. In general, suppose we have
th of the traffic. In general, suppose we have 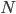 cars, then each one of them controls
cars, then each one of them controls 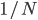 th of the traffic. This way, as N becomes very large, the fraction
th of the traffic. This way, as N becomes very large, the fraction 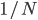 becomes very small, hence, an individual driver has negligible influence on the system, only large groups of cars have. This reasoning allows us to aggregate drivers' decisions by only considering what fraction of the flow goes into each path. These fractions determine flows on the road sections. Just like a water flow splits and merges when traversing bifurcations in a river.
becomes very small, hence, an individual driver has negligible influence on the system, only large groups of cars have. This reasoning allows us to aggregate drivers' decisions by only considering what fraction of the flow goes into each path. These fractions determine flows on the road sections. Just like a water flow splits and merges when traversing bifurcations in a river.
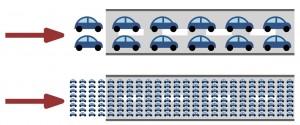
Two car flows with different levels of congestion (figures by Neil Olver).
The second assumption we make is that all drivers have full information of the state of the network. This will allow them to make informed (selfish) decisions. As mentioned in the introduction, the availability of real-time navigation systems makes this assumption reasonable. However, a fair amount of research is focused on what happens when this assumption does not hold, which is beyond the scope of this article.
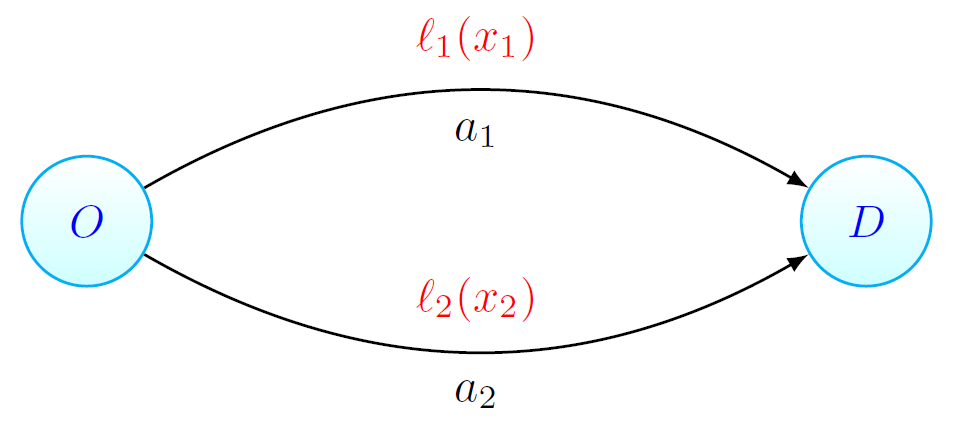
To introduce some of the challenges of modeling congestion and selfish behavior, let us begin with the simplest example: a double arc parallel network (also known as Pigou's example), as in Figure 2. In this network, the two arcs 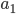 and
and 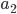 connect an origin
connect an origin 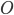 with a destination
with a destination 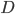 , however, these two ways of traveling might lead to different travel times, this due to different congestion levels, but also because the two roads may be qualitatively different.
, however, these two ways of traveling might lead to different travel times, this due to different congestion levels, but also because the two roads may be qualitatively different.
We quantify the travel time of the arcs by latency functions: if a fraction 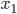 of the drivers use arc
of the drivers use arc 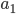 , then
, then 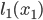 represents the time it will take to them to reach their destination; similarly, if a fraction
represents the time it will take to them to reach their destination; similarly, if a fraction 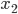 of the drivers use the alternative arc
of the drivers use the alternative arc 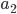 , then
, then 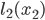 represents their travel time. Naturally, the higher the fraction of users on a road the higher its travel time, so we will assume that
represents their travel time. Naturally, the higher the fraction of users on a road the higher its travel time, so we will assume that 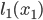 and
and 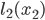 are increasing with respect to
are increasing with respect to 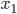 and
and 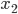 , respectively.
, respectively.
Let us think for a moment on what the government would want to happen in this network. An efficient use of the network means to minimize the average travel time, which in this case can be expressed as the minimization of 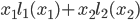 , where
, where 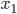 is the fraction of travelers that use
is the fraction of travelers that use 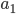 , and
, and 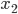 is the fraction of travelers that use
is the fraction of travelers that use 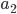 ; as they are fractions, we may impose that
; as they are fractions, we may impose that 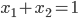 and that they are non-negative, i.e.,
and that they are non-negative, i.e., 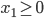 and
and 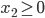 . This situation is what we call the social optimum.
. This situation is what we call the social optimum.
For our example let us take 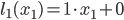 and
and 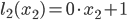 . In this way, we get
. In this way, we get 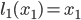 and
and 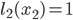 .
.
https://networkpages.nl/CustomMedia_old/Animations/SimpleStuff/TrafficPigousExample.html
Exercise 1: What values of 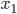 and
and 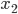 minimize the average travel time, i.e., give the social optimum?
minimize the average travel time, i.e., give the social optimum?
Drivers in general do not care about the social optimum. They are only interested in minimizing their individual travel time. What type of flow can we expect to see in the network as a result of this selfish behavior? Or said differently, how will the flow spread out over the network if we assume all drivers are selfish? Suppose a driver uses arc 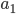 , but that the latency on
, but that the latency on 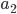 is lower. As a result the driver could improve its travel time by switching to
is lower. As a result the driver could improve its travel time by switching to 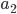 . A driver will not switch if the latency on
. A driver will not switch if the latency on 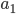 is lower or the same as that of
is lower or the same as that of 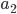 . Therefore, this means that if there are drivers on
. Therefore, this means that if there are drivers on 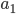 , then the latency on
, then the latency on 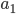 must be lower or the same as that of arc
must be lower or the same as that of arc 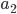 . Mathematically speaking, if
. Mathematically speaking, if 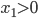 , then
, then 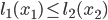 . The same holds for arc
. The same holds for arc 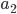 : if
: if 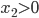 , then
, then 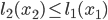 . These are called equilibrium conditions, and a flow satisfying them is called an equilibrium flow.
. These are called equilibrium conditions, and a flow satisfying them is called an equilibrium flow.
Exercise 2: For what values of 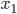 and
and 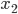 do we have
do we have 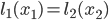 ? It turns out that these values of
? It turns out that these values of 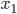 and
and 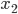 give an equilibrium. Check this using the equilibrium conditions. What is the average travel time?
give an equilibrium. Check this using the equilibrium conditions. What is the average travel time?
As you can see from Exercises 1 and 2, the travel time in the case of selfish drivers is worse than that of the social optimum (which is preferred by the government). This inefficient usage of the road network is expressed by the Price of Anarchy (PoA), defined as the ratio of the average travel time in the (selfish) equilibrium, and the average travel time in the social optimum.
Exercise 3: What is the Price of Anarchy for the latency functions as in Exercise 1 and 2? Now, choose different latency functions in the animation, and determine the social optimum and equilibrium. Can you get the Price of Anarchy worse than that of Exercise 1 and 2?
Referenties
- Tim Roughgarden and Éva Tardos. 2002. How bad is selfish routing?. J. ACM 49, 2 (March 2002), 236-259.

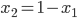
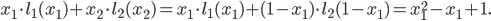
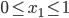
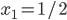
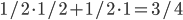
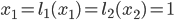
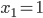
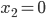

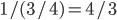
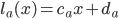
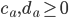
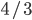
![[1]](https://www.networkpages.nl/wp-content/plugins/latex/cache/tex_35dba5d75538a9bbe0b4da4422759a0e.gif)