Below a poster about Structure in social networkswhich was made for mathematics exhibition IMAGINARY. This poster was made by Clara Stegehuis, assistant professor at Twente University.
Communities in social networks
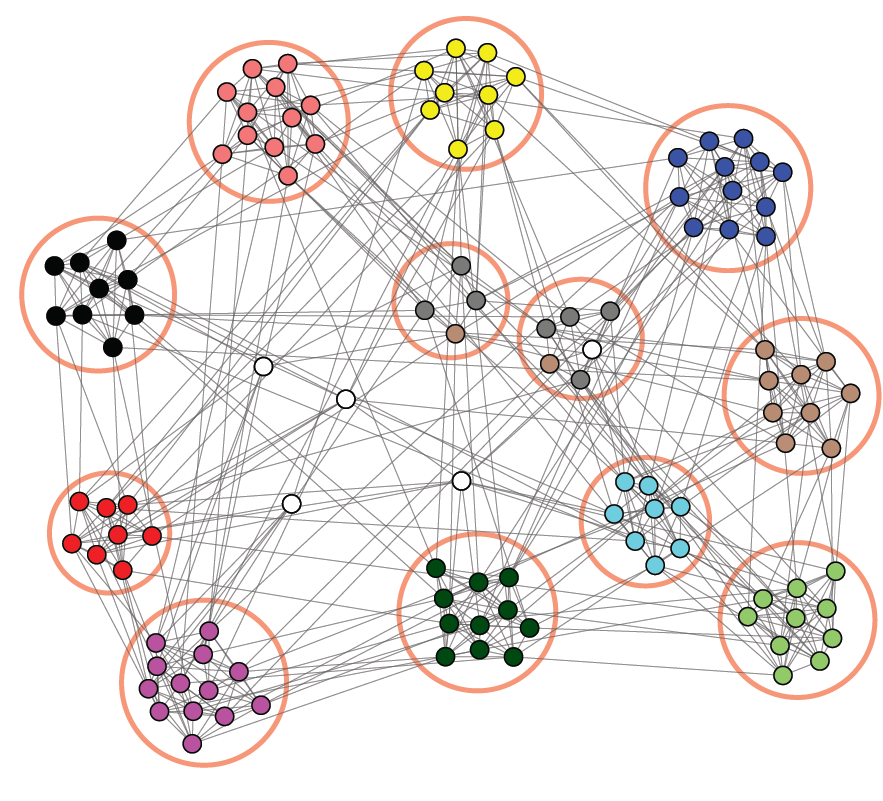
Before you can start looking for the network communities, we first have to know what a community is. The poster suggests that a community has the following properties:
- There exist relatively many connections between nodes in the same community.
- There exist relatively few connections between nodes in different communities.
To find the network communities, we need a mathematical equation that describes when a division of the network into communities meets these two criteria. One of the first such equations, the so-called modularity equation, uses exactly these two community properties.
Suppose we divide a network into several groups. Then the modularity of this network division is an equation with two terms. The first term counts the number of connections within all groups. In short, this says that we would like to have as many connections as possible within the groups. Unfortunately, only maximizing this term will not help.
If we only maximize the number of connections within the groups, then the best division is to put all nodes of the network into one large community. In that case, all network connections are within the same community. To overcome this problem, the modularity equation subtracts a second term from the first term.
This second term describes the expected number of connections within each group if we would redraw the network with the same number of connections per point, but make the connections randomly. Then the division into only one community is not too good anymore. For only one community, we already expected that all connections are within that same community, so the modularity of the one single community is equal to zero. Modularity, therefore, measures how many more connections there are within the communities than we actually expected.
Feel free to print and use this poster for educational purposes. Since this material is protected under a Creative Commons licence we ask you to mention Anna Priante and the Network Pages when using it.
Are you one of those people who always seems to pack just a bit too much for your car to handle when packing for a vacation? Then you should have a look at this article!
Imagine you’re in a remote village and only have a limited number of vaccines to distribute to protect the community from a deadly virus, who do you vaccinate?
A difficult decision, but necessary. Assuming that the disease is just as deadly for everyone in the community, the best way to prevent deaths is to contain the spread of the virus.
In this article, we will discuss a mathematical riddle that "seems impossible even if you know the answer". It is better known as the 100 prisoners problem.
