Is a rapidly mutating virus unstoppable?

How playing games and stepping through multiple fields of research makes a reliable answer inevitable.

My grandmother was born a long time ago and grew up in a world that does not exist anymore. Among farmers in the small german village Kerwienen (today’s Kierwiny in northern Poland). A world in which women had to work in the household and were not allowed to pursue their education. A time during which interpersonal abuse and violence were not rare. Especially for teenagers coming as refugees to western Germany. Experiences that hardened her heart and mind to stay a survivor forever.

Any virus appears to be trapped in similar chaos. A virus cell made up by a single microbe is only a few nanometers tall and is faced by much larger adversaries. That’s the same magnitude of size difference as comparing a human to the sun. Moreover, in general all ancestors of a virus pass away before its offspring can travel the world. Hence, there is not much space or time for a virus to develop, something we appreciate as humans trying to stay healthy.

During my time in highschool, I visited my grandparents every Saturday morning. To help my grandfather in the workshop, clean the roof of their house, cut down plants in the garden, etc. As their health didn’t allow them to do any of these things themselves, it was always a day of relieve for them. It mirrored my early childhood, with reversed roles. There was a lot of emotional trauma in both of my grandparents lives which they refused to ever address, but every now and then during lunch something spilled out and we were able to sort out a piece of the puzzle of what was causing distress.

A virus lacks many such complexities of humans. It has a simple mind and nothing that we would call emotions. Actually, a microbe contains only a code, called the genome, carrying not much more than the information required to replicate itself. We humans carry a lengthy DNA which encodes how every cell in our body should be designed and replaced once it dies. Moreover, we are able to mate with other humans to create the DNA of a new human composed of 50% of the DNA of each parent. In contrast, a virus has to take advantage of a host to create nothing more than a simple copy, usually killing cells of the host in the process. The solution to stop these tiny objects from killing more of our cells than we can restore seems obvious: learn the code they use to harm us and intervene in the replication process with a cure.

Ending the story here we only overlook the minor detail that decoding an intruder like a virus is a delicate task. Not only do we need to make no mistakes in finding and applying a cure. A successful restoration of the cells under attack is dependent on the virus not changing its strategy in the last (nano)second. To not attribute a strategic mind to a virus we perceive any deviation from its expected replication behaviour as an error. Such errors, called mutations, are a simple natural phenomenon we can observe in any species. Unfortunately, mutations can cause a major problem arising from a difference in size. For example, an assailant like Covid19 can mutate two million times faster than a human. If these mutations produce a variant of the virus that is particular harmful to humans as Covid19 was able to do it, a pandemic emerges. This leaves us with two contradictory objectives: precision and speed. We want to find a medicine which accurately starves off virus cells and do so extraordinarily fast. Otherwise new mutations can occur during the development of a cure which might render it ineffective or even useless. However, there are limitations on how low the computational cost to decode a virus can be. How can one hope to understand the precise structure of a virus if it is able to become unrecognizable within weeks?

The mathematics behind this questions didn't let go of my mind for extensive periods of time during my PhD studies in Belgium. Not because I figured it was an important question that needed to be addressed (the project started before the pandemic of 2020). Rather it’s a question that I can not ignore. One of these activities you keep coming back to because your mind would not let you abandon it. Like another one of the large jigsaw puzzles I as a child put together with my grandmother where you do not give up just because you are faced with 200 almost identically looking blue pieces.

The life of a virus is so chaotic, it sounds foolish to try to unravel the precise mechanisms that explain the patterns of mutations of its evolution. To look for statistical regularities seems more sensible. Indeed, that is what professionals tend to do. For example, the network depicted on nextstrain.org attempts to explain how the first few cases of Covid in 2019 from Wuhan evolved into the viral variants of the virus found everywhere in the world. In the following figure you can see a possible explanation of how the genomes of SARS-CoV-2 evolved over the past 6 months and how many mutations occured in this period.

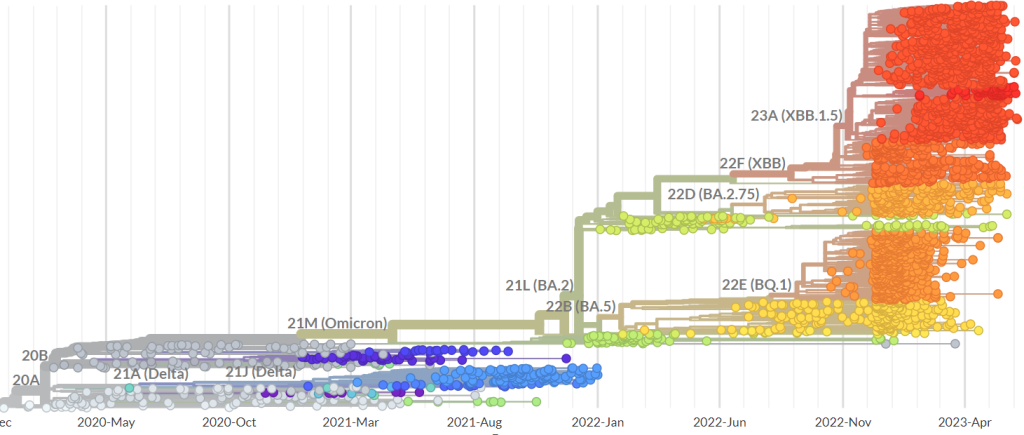
For the sake of brevity I won’t go beyond the simplest form of such a network. Therefore, you can think of edges in an evolutionary network the same way you would look at edges of your family tree. Any two members of your family have a common ancestor, connected by a path of edges in the tree. The same holds (hypothetically) for a family of viruses. Statistical regularities can be sufficiently strong to classify the variants of a virus accurately by an evolutionary network and therefore enable us to decode similar variants in the network more efficiently. However, I want to investigate the fundamental rules governing the life of a virus that allow us to produce evolutionary networks which are not only accurate coincidentally, but accurate with certainty. This is where the ability of the virus to become unrecognizable quickly creates challenges.

After I went abroad it became clear that my grandmother had Alzheimers. Something that must have been there with her for a long time but which became impossible for her to hide anymore. At the time I traveled back she understood I arrived from a different place she hasn’t been to. However, places and time changed multiple times during our conversations. Fortunately, being forced to forget the troubles of her past lightened her mood and took weight off her shoulders. She became less hardened, not only around me but also around others. Only the confusion brought by the disease kept her puzzled, leading to the painful realization that there was no path for me to go back in time to the full person she once was.

In 1967, an article titled Phylogenetic analysis: Models and estimation procedures introduced to geneticist how one can view evolutionary networks as accurate models of evolution without paying attention to the dimension of time. This meant to decode a virus looking back into the past was no longer a requirement. In other words, we want to apply methods to data available to us today to classify it without knowledge about when mutation events took place. Indeed, going back in time does not lower the complexity of building an evolutionary network and does not offer us additional support in decoding viruses from today's data. How could a timeless estimation procedure of an evolutionary network look like?

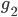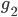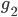Take a dataset of genomes which contains a measurement of the amount of evolution separating each pair of genomes, called the evolutionary distance. For example, for pairs of genomes $g_1$ , $g_2$ , one possible such measure is the number of mutations one can count to transform genome $g_1$ into $g_2$ . 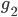If the two genomes $g_1$ and $g_2$ are at a minimal evolutionary distance among all alternatives involving $g_1$ or $g_2$ , then you call them neighboring. Now, play the following game: take a pair of neighboring genomes. Then, the data suggests that they share an ancestor. Create an artifical genome for this hypothetical common ancestor, and replace the pair in the dataset with this artificial genome. So, the ancestor takes the place of its offsprings. Continuously join such neighboring genomes until you obtain a network connecting all genomes through their common ancestors.

For example, instead of viruses, consider my genome and the genomes of my sister, brother, mother and uncle represented by the blue nodes in the figure below on the left. The dataset shows that we all have neighbouring genomes, suggested in the figure by connecting all the blue nodes with yellow node in the middle. Then, joining neighbours might produce the network shown on the right here:

Figure 1

First, you consider all genomes on the left and choose the most similar pair. Suppose the data suggests that my genome and that of my sister are the best choice. Then, you can infer that me and my sister have a common ancestor, hypothetically our father, and therefore you need to consider the network in the middle of Figure 1. Make the same decision here again, this time choosing the genomes of my mother and uncle to infer that their common ancestor might be my grandmother. Then, there is only one original genome left unprocessed, the one of my brother. Thus, you are finished with the neighbor joining construction of an evolutionary network.

The neighbor joining method can be extended to create more complex structures, too. For example, the data might suggest that separating the genomes of me, my mother and uncle from the genomes of my sister and brother, as well as keeping me and my sister’s genome at a high evolutionary distance from the rest leads to a better explanation of evolution:

Figure 2: It can be that another method than the neighbor joining method gives a better explanation of evolution.

However, keep in mind that the method I have sketched just now aims at explaining the evolution of viruses, not humans, i.e., the constructed network is accurate only if organisms can self-replicate and all hypothetical common ancestors have gone extinct.

In the end, after her mind had forgotten everything, my grandmother passed away during springtime. I don’t remember much about the funeral or the events surrounding it. It was during the crisis period of my PhD when my mind got stuck on multiple problems beyond network design that I could neither solve nor let go off. It is always a pity when desires are just out of reach. Whether a research question remains unanswered or an old friend vanishes indefinitely.

The question of how to make optimal choices to join genomes in a network as I have just described will stay an unanswered mystery for longer among many more prominent computational problems (see this post if you want to learn more about computational complexity and the P vs NP problem). Luckily, there is a path in-between the powerful forces of inaccuracy and intractability which leaves you unscathed in the quest of understanding the fundamental forces of life.

Let me introduce some integer numbers to describe the structure of an evolutionary network. For example, count the minimal number of edges separating two genomes in a network. Then, in the case of three genomes, you can view these integers as vectors in a 3-dimensional space. To illustrate, consider the following figure:

Figure 3

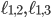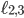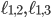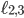Here, $\ell_{1,2}, \ell_{1,3}$ and $\ell_{2,3}$ denote the minimal number of edges in a network separating genomes 1 and 2, 1 and 3, and 2 and 3, respectively. Therefore any point in this space assigns a non negative number to $\ell_{1,2}, \ell_{1,3}$ and $\ell_{2,3}$ , i.e., every point specifies an evolutionary network on genomes 1; 2 and 3. Then, the green plane includes all the points for which 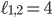$\ell_{1,2} = 4$ and the yellow plane all the points with 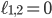$\ell_{1,2} = 0$ . Hence, in-between the two planes lie all the points for which 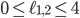$0 \leq \ell_{1,2} \leq 4$ . Some points in-between the yellow and green plane might not be meaningful in identifying an evolutionary network. For example 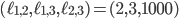$(\ell_{1,2}, \ell_{1,3}, \ell_{2,3}) = (2, 3, 1000)$ specifies an integer point in the region 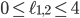$0 \leq \ell_{1,2} \leq 4$ . However, there exists no network realizing these distances between genomes 1, 2 and 3 because 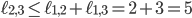$\ell_{2,3} \leq \ell_{1,2} + \ell_{1,3} = 2 + 3 = 5$ . Then, include this last inequality in the description of evolutionary networks by only considering points in between the yellow and green planes and above the red plane, cutting off the point 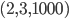$(2, 3, 1000)$ , in the following figure:

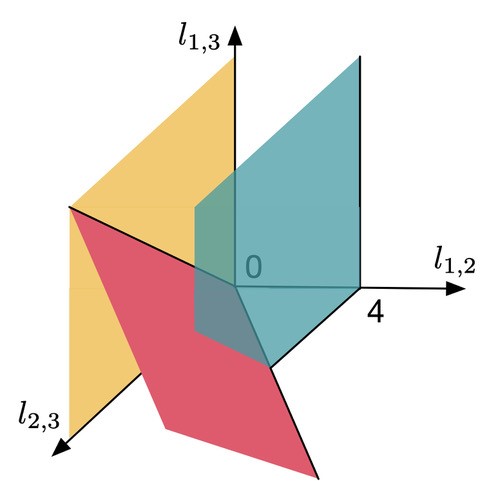
Figure 4

Among all integer points one aims at finding the one identifying the true network explaining an evolutionary process. Even though this problem is theoretically intractable, well thought out restrictions on candidates of integer points can get you reasonably close to good solutions (see this book for further reading). Indeed, often in such problems mathematicians try to define variables and come up with equations and inequalities which encompass important characteristics of the network they try to study. For a given set of networks, one calls finding the "best" description of the type shown in Figure 4 a compact description (if you are interested in what compact precisely means you might look into books like this). Compact descriptions establish a link between geometric and algebraic properties of a problem. From the point of view of an engineer a compact description allows for the development of methods to improve the solvability of problems like finding the most accurate evolutionary network. An example of such an insight is the following:

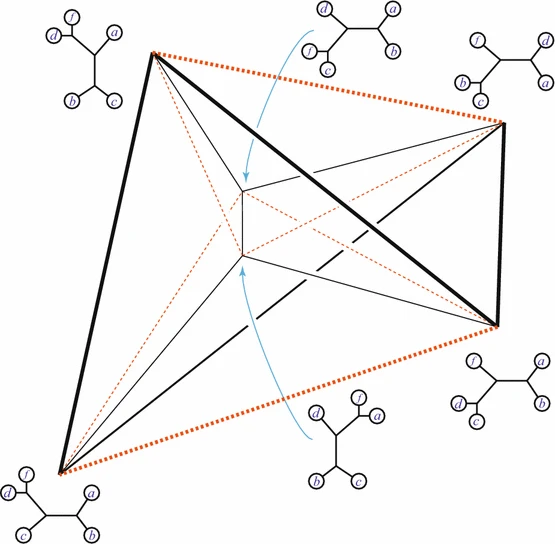
Figure 5: The Bitkhoff polytope. Image taken from this article.

Here you see the so-called Birkhoff polytope in four dimensions, a geometric object you obtain by glueing together a collection of triangles in a particular way. Since it is hard to imagine how 4 dimensional objects look like, Figure 5 shows a projection into 3D without paying too much attention to how the points connected by the black and red lines should be placed in a 3D space like in Figures 3 and 4. Notice that each one of the triangles can be described by a plane defined by its three vertices, similar to how we described the red plane in Figure 4 by three variables. The important observations here is that, like in the last example, every vertex of the Birkhoff polytope is an integer point specifing the minimal number of edges between all pairs of genomes 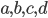$a, b, c, d$ and $f$ in a family-tree-like network. A graphical representation of the network is shown next to each of the vertices. 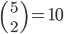If you are interested in understanding why 4-dimensional vertices are sufficient to describe ${5 \choose 2} = 10$ evolutionary distances between distinct pairs of genomes in each network you might look into this article.

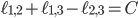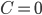It is proven that the Birkhoff polytope is part of a compact description of all family-tree-like evolutionary networks on 5 genomes (see this article for details). Consider again the red plane in Figure 4, written as $\ell_{1,2} + \ell_{1,3} - \ell_{2,3} = C$ for $C=0$ . This plane can be described as a linear function in three independent variables. Therefore, you can look at the intersection of the plane with the Birkhoff polytope for any real number 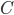$C$ . 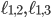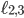Since all vertices of the Birkhoff polytope are integer, this view allows us to find an integer point including variables $\ell_{1,2}, \ell_{1,3}$ and $\ell_{2,3}$ which describes a family-tree-like evolutionary network on genomes 1 to 5 by maximizing or minimizing 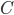$C$ (For this example the network has to fit into one of the 6 different networks shown in Figure 5). This is the key feature of a compact description, breaking down the difficult question of identifying integer points with respect to some selection criterion into the easier question of solving a linear optimization problem. Even when such a translation of the problem can not be fully done (for example for evolutionary networks on at least 6 genomes) insights into the combinatorial structure of networks lead to a better understanding of what makes solving a particular problem difficult.

The beauty of these kinds of insights into the combinatorics is that they lead to elegant mathematical formulations of the problem. Furthermore they can also be engineered to enhance the quality of solutions produced by simple and fast methods like neighbor joining. In doing so you neither loose the accuracy of the model nor reach intractability for a vast number of datasets you encounter in reality. In the end, can this approach (with enough research) succeed in dismantling any virus? I don’t know, but if we keep our attention on the true nature of the forces acting on us, then scientists as well as broader human communities will keep building systems that will stand the test of time.

The featured image is from Pixabay by Alexandra Koch.

Would you like to stay up to date when a new post appears on the Network Pages?

Subscribe to our mailing list