Some ideas on teaching graph theory in high schools

Have you ever wondered how you can make mathematics interesting to the daily life of students? Which mathematics teacher has not been confronted with the question: $``$ Why do we need to learn mathematics? $"$ at least once in their career? In this article, we will discuss two important and exciting concepts teachers can use to introduce graph theory in their classes, which is one of the fields in mathematics with applications in $``$ the real life of students $"$ . In this way, students can see why and how mathematics is important in daily life applications.

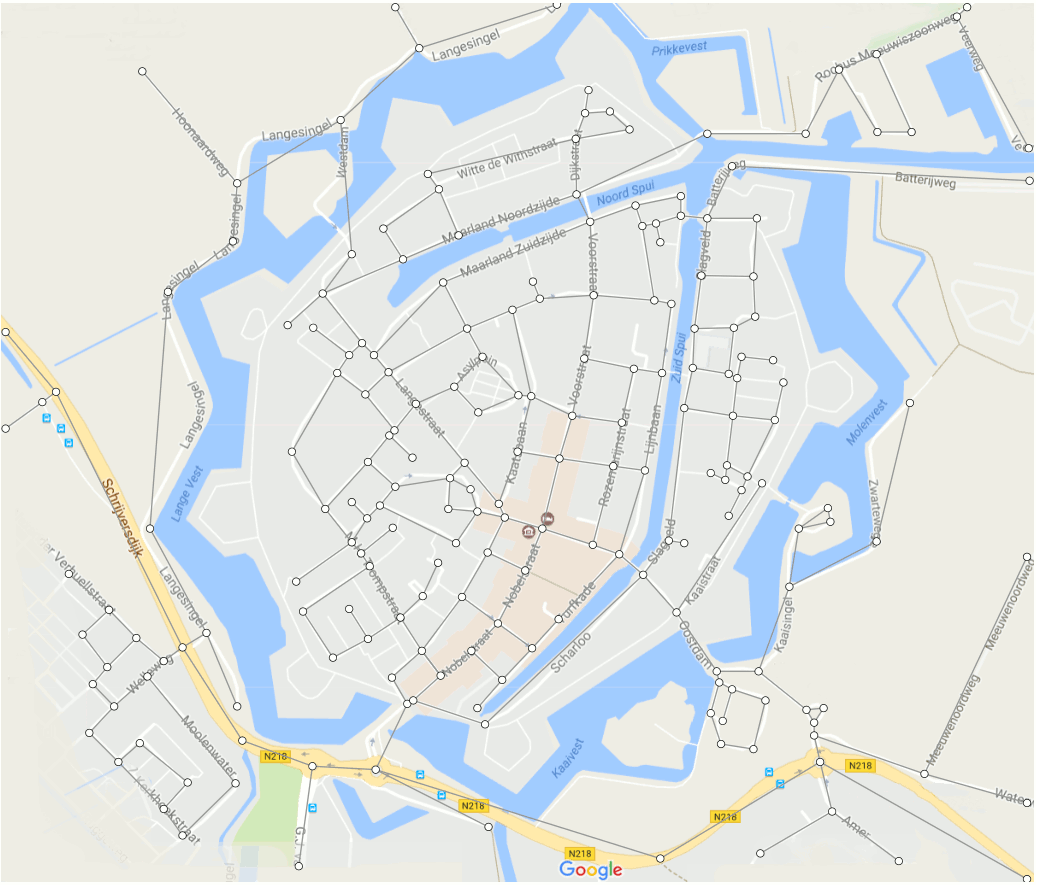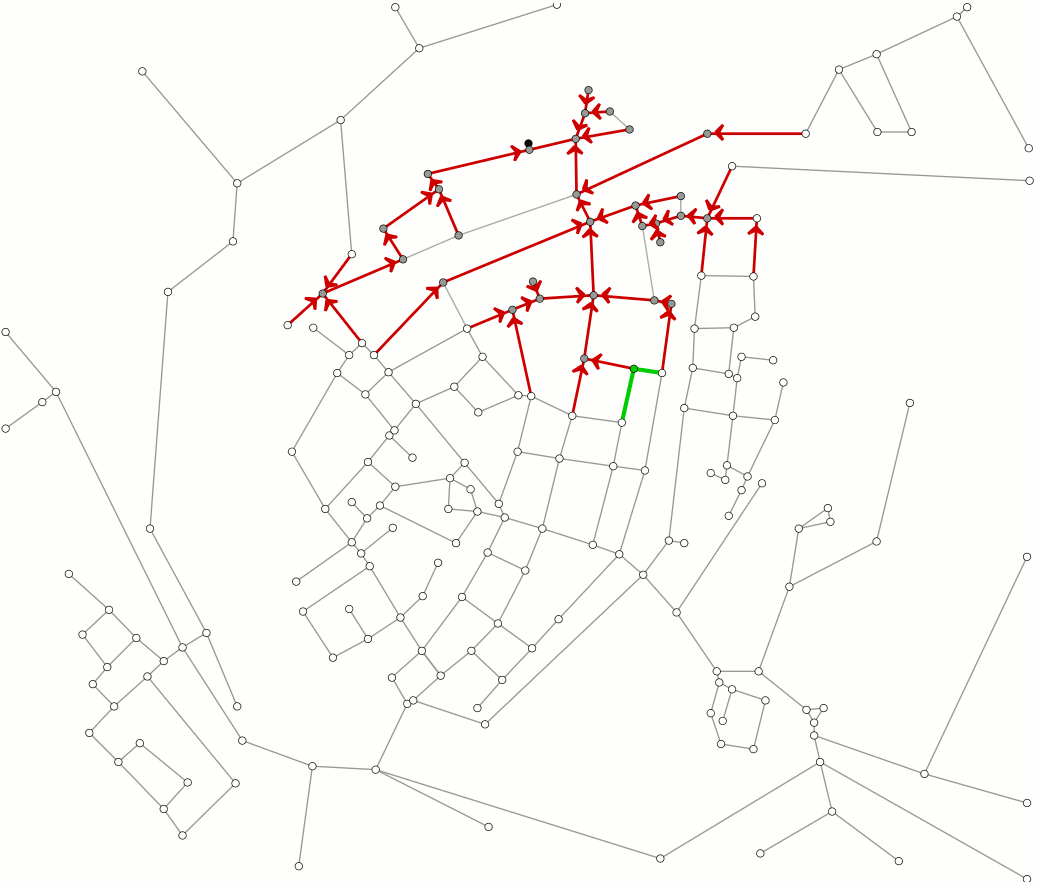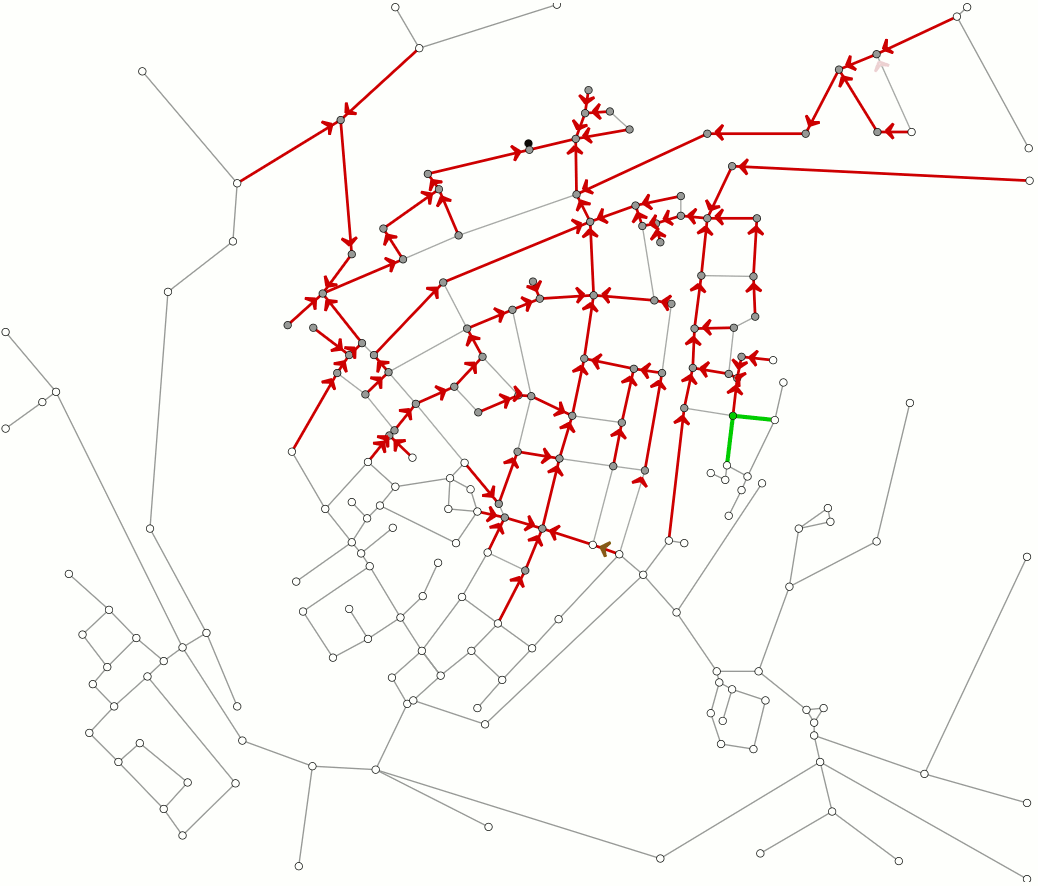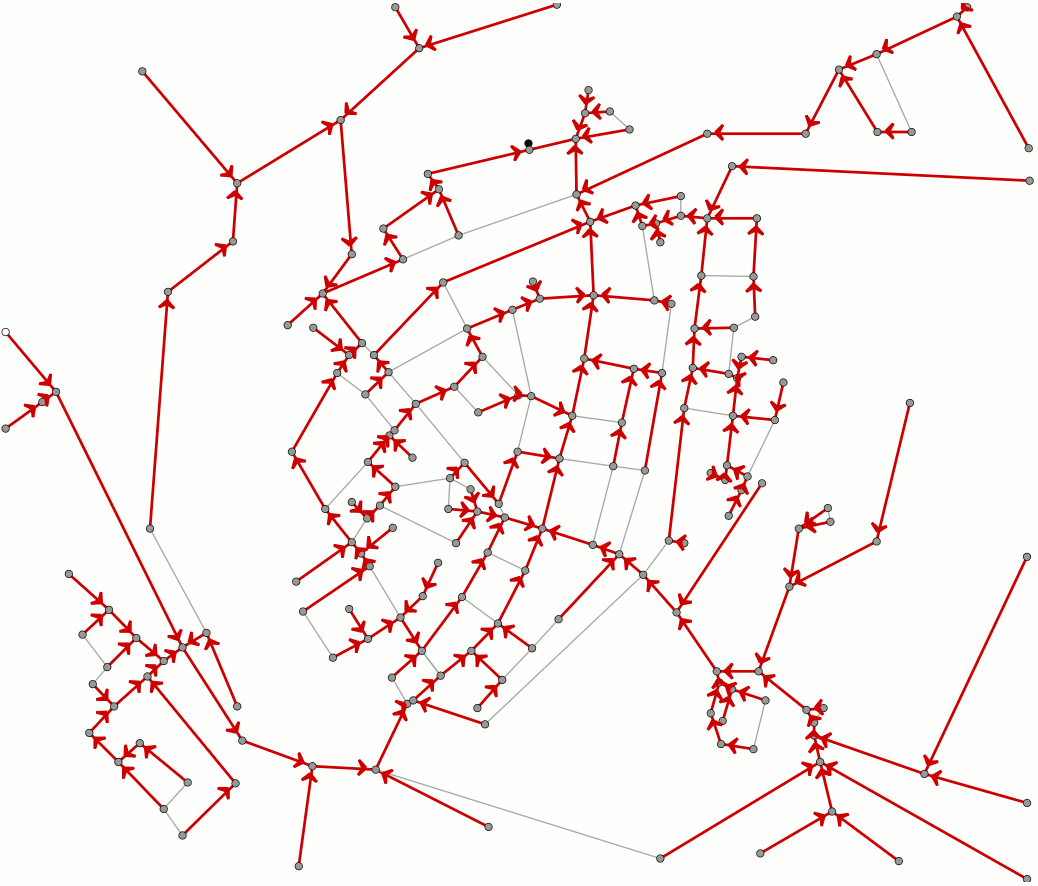
As its name suggests graph theory is the branch of mathematics that studies the properties and structure of graphs. Before we discuss the definition, let's start with some examples. Think of the railway network connecting train stations, the network of highways connecting cities, and even your own Google Maps which calculates the fastest route to get you from home to your work.

In general, a network consists of objects with connections between them, and possibly also properties of the objects and their connections. In mathematics, a network is called a graph, the objects are called vertices (or nodes), and the connections are called edges. Edges can also have weights, which are numbers that can represent, for example, distances or travel times.

The shortest path algorithm

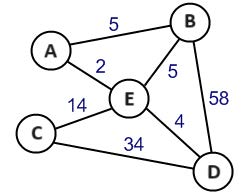
Have a look at the figure on the right. This is an example of a fairly simple graph. We let the numbers represent the distances between cities A, B, C, D, E. A classical question in graph theory is how to compute the shortest route between two nodes in such a weighted graph. To find the shortest route from city A to C, you can calculate the distances of all the routes.

But if we look at even more cities and possible routes between them, we get something like the network in the figure below, where obviously the complexity increases. If we were to calculate all distances separately, we would become utterly miserable. By treating this as a graph theoretical problem, we find that there is a simple algorithm we can use to find the shortest route between cities: Dijkstra’s algorithm.

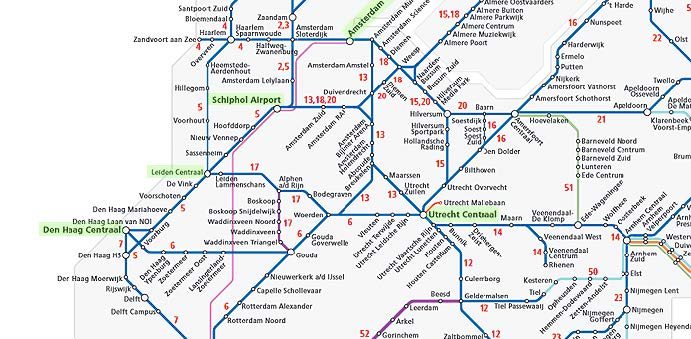
The trainrail network of the Randstad in the Netherlands.

This is one example someone could use to implement graph theory in their lessons. However, the potential of graph theory extends beyond finding shortest routes. Let us look at another topic in graph theory: coloring graphs.

Coloring graphs

Why would one be interested in coloring graphs and what do we even mean by that? Let us first discuss the why: A map of the world is always displayed with different colors for different countries. But what if we wanted to do this with as few colors as possible? This is where graph theory comes around the corner. In graph theory we can look at the minimum amount of colors needed for coloring a graph such that vertices sharing an edge don't get the same color. This number is called the chromatic number of the graph. Calculating the chromatic number is usually a really hard problem. (On the Network Pages you can find a whole list of articles on this topic.) Yet it’s an engaging challenge that can captivate students’ imagination. We can calculate it for easy graphs like the one at the beginning of the article (you can do this as an exercise!).

But how can we go from maps to graphs? We first identify the countries with nodes. If two countries share a border, they are connected by an edge in the graph. Then we can color the nodes of the graph using the least amount of colors and making sure no vertices sharing an edge get the same color. Afterwards, we color the countries with the corresponding color of the node, so we get something like the figure on the right.

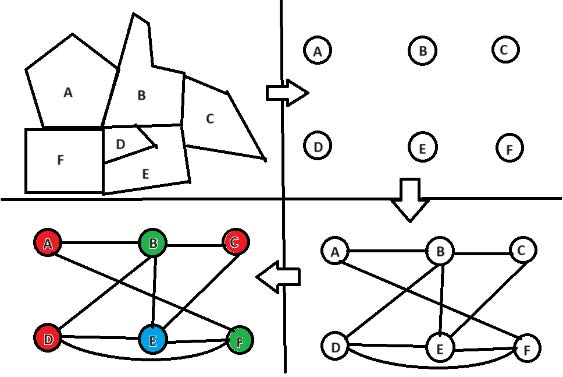
An example of how to color a map using graph theory.

We see that we can use graph theoretical problems to show students not all topics in mathematics are solving boring equations. In fact, they can be pathways to understanding and shaping the world around us. And that some parts of mathematics are even applicable to their daily life. So instead of $``$ Why do we learn this? $"$ we will hopefully get the question: $``$ Is there more to learn? $"$ .

If you would like more material related to graphs, networks, and algorithms to teach such a subject in your class then you can use the booklets written for the annual masterclasses NETWORKS goes to school!

Would you like to stay up to date when a new post appears on the Network Pages?

Subscribe to our mailing list