Imagine you want to send a letter to a friend across the country. After you put it in the mailbox, it seems to magically appear at their door. Of course this is not magic: it goes from your local post office, to a regional sorting center, then to another, and eventually to your friend's local post office before arriving. At each step, someone handles the letter and sends it on its way.
The internet works in a very similar way. When you send data from your computer - for example to load a webpage, stream a video or send a message - this data has to follow a certain route. It travels across a series of interconnected devices, called routers. Each router acts like a mini-post office, receiving your data packet and forwarding it to the next router on the path to its final destination.
To understand how the data travels over the internet, we can use TRACEROUTE. You give TRACEROUTE a destination, like google.com, and it then finds the entire journey your data takes to get there. It shows you every single router (a node) along the path, from your computer all the way to the destination.
But imagine that you don't want to know only how your letter travels to your friend, you want to know how all letters travel through the network. Then, instead of a single path, we will get millions of paths over millions of nodes. And every day, this network might change: making it very hard and time-intensive to find the complete network.
In this article we will have a look at the graph reconstruction problem. If I give you a set of nodes, how can you find all connections (edges) between these nodes as efficiently as possible? There are some rules: you only know that there are  nodes in the graph, and you can only ask so-called 'queries' to me (or the 'graph oracle'): questions about properties of graph.
nodes in the graph, and you can only ask so-called 'queries' to me (or the 'graph oracle'): questions about properties of graph.
Today we are interested in shortest-path-distance queries. Suppose we have the following network:

If we ask a query about node 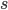 and
and  , we are given the distance of the shortest path between these two nodes, which we denote by
, we are given the distance of the shortest path between these two nodes, which we denote by  . This shortest path distance is the minimum number of edges we have to traverse to go from
. This shortest path distance is the minimum number of edges we have to traverse to go from 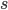 to
to  . You can imagine this shortest path is very useful: this is also how we navigate the world. If want to know more about finding shortest paths, check out this article or this one!
. You can imagine this shortest path is very useful: this is also how we navigate the world. If want to know more about finding shortest paths, check out this article or this one!
Thus, in this case we have  . This means there is no edge between
. This means there is no edge between 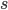 and
and  , since the shortest path from
, since the shortest path from 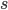 to e contains
to e contains 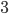 edges. If the distance between two nodes equals
edges. If the distance between two nodes equals  , however, there must be an edge between those nodes.
, however, there must be an edge between those nodes.
We want to find a strategy to find all edges in the graph with as little queries as possible. A simple upper bound on this number of queries is  : we perform a query for every node (of which there are
: we perform a query for every node (of which there are  ) with every other node (of which there are
) with every other node (of which there are 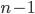 ), although we now count every node twice, so we can divide by 2. This totals
), although we now count every node twice, so we can divide by 2. This totals  queries. For a network of 5 nodes, this means we have to do
queries. For a network of 5 nodes, this means we have to do  queries, which is very doable. However, if we want to find all edges in an internet network with
queries, which is very doable. However, if we want to find all edges in an internet network with  nodes, we would have to do
nodes, we would have to do  queries. Suppose a query takes 1 second, then this means we would be querying more than 578 days!
queries. Suppose a query takes 1 second, then this means we would be querying more than 578 days!
Can we reduce this number of queries? Could, somehow, just a handful of queries be enough? No! In any case, we have to perform 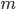 queries: one for each edge. This is because, as long as you do not query an edge, we cannot not know whether it exists or not.
queries: one for each edge. This is because, as long as you do not query an edge, we cannot not know whether it exists or not.
So we have a theoretical lower bound (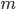 queries), and an upper bound (
queries), and an upper bound ( queries). We want to find a smart way of finding all edges in a network, which is as close to the lower bound as possible. This means that the algorithm should query as few non-edges as possible. Let's first focus on general, bounded-degree graphs. Bounded degree graphs are graphs for which every node has at most
queries). We want to find a smart way of finding all edges in a network, which is as close to the lower bound as possible. This means that the algorithm should query as few non-edges as possible. Let's first focus on general, bounded-degree graphs. Bounded degree graphs are graphs for which every node has at most  edges, where
edges, where  is a constant (a fixed number). This is not important for now, but it is important if you want to prove the results that I will show you. Later, I will show an extension of the algorithm for geometric random graphs where every node has a location in space.
is a constant (a fixed number). This is not important for now, but it is important if you want to prove the results that I will show you. Later, I will show an extension of the algorithm for geometric random graphs where every node has a location in space.
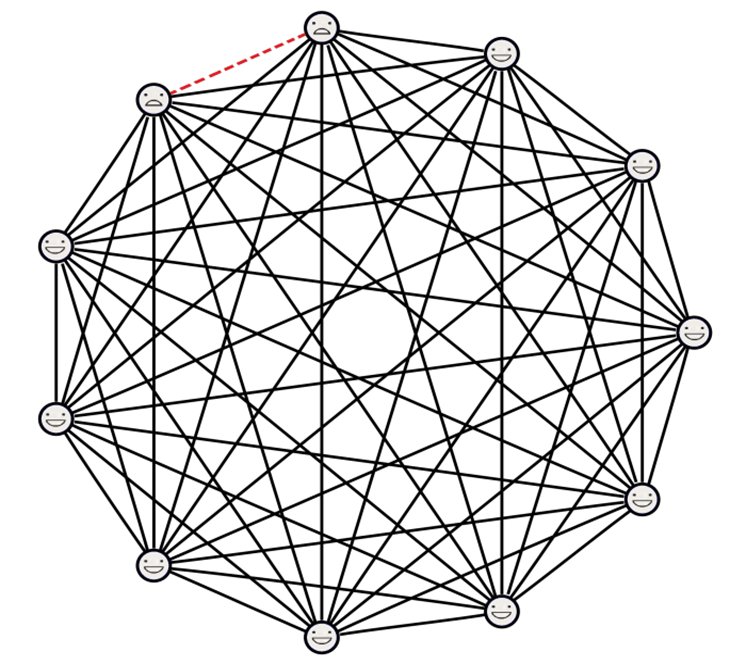
For general bounded degree graphs, Mathieu & Zhou proposed the SIMPLE algorithm1. The general idea of this algorithm is to start with a complete graph with potential edges and eliminate all potential edges that cannot exist in the real graph. So, the algorithm goes from this graph:

To this graph:

We can eliminate these potential edges by doing queries. Let's look at the example graph above. We focus on nodes  and
and  in the figure. Suppose that we know the following:
in the figure. Suppose that we know the following:
 , and
, and
From these two queries, we can deduce three things:
- There is an edge between node
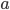 and node
and node 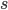 ,
, - There is no edge between node
 and node
and node 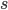 , and
, and - There is no edge between node
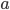 and node
and node  .
.
The first two observations follow directly from the two queries: a shortest path query of  tells us there is an edge and a shortest path query of
tells us there is an edge and a shortest path query of 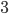 tells us there is no edge. This last observation follows from the two queries together. Suppose there is an edge between node
tells us there is no edge. This last observation follows from the two queries together. Suppose there is an edge between node 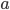 and node
and node  . Then we could go from
. Then we could go from 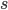 , to
, to 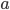 , to
, to  using only two edges. So
using only two edges. So  This is not possible, because the query tells us that
This is not possible, because the query tells us that  . Therefore, there cannot be an edge between node
. Therefore, there cannot be an edge between node 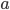 and node
and node  .
.
Thus, we have confirmed one potential edge and eliminated two! The state of our algorithm at this point is:

Here, red means an edge has been eliminated (it cannot exist) and green means the edge exists.
Now, let's generalize this observation: we can eliminate all potential edges between nodes 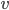 and
and 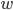 for which \begin{equation} |d(v, s) - d(w, s)| > 1. \end{equation} In other words: we can eliminate all potential edges if the difference between their shortest paths to some node
for which \begin{equation} |d(v, s) - d(w, s)| > 1. \end{equation} In other words: we can eliminate all potential edges if the difference between their shortest paths to some node 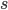 is larger than 1.
is larger than 1.
After these two queries, let's do two more queries:
 , and
, and .
.
Since the shortest path from b to s and from c to s is larger than 1, we again can eliminate both potential
edges.

Now, there are only 4 potential edges left, which we will query directly. In total, we have done the following 8 queries to obtain the full graph:
 ,
,  ,
, ,
,  ,
,  ,
,  ,
,  ,
,  .
.
In total, we performed 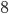 queries for this graph of
queries for this graph of  nodes. Now you may notice that we start querying distances to
nodes. Now you may notice that we start querying distances to 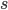 . Why did we choose a 'special' vertex
. Why did we choose a 'special' vertex 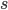 ? In the SIMPLE algorithm, we choose approximately
? In the SIMPLE algorithm, we choose approximately  of these nodes
of these nodes 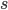 and call this the seed set
and call this the seed set 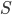 . This seed set is just a random subset of all the nodes in the graph. We call these seeds as we start with these nodes and do a query with these seeds against all other nodes in the graph. This gives us a starting point to eliminate edges. 2
. This seed set is just a random subset of all the nodes in the graph. We call these seeds as we start with these nodes and do a query with these seeds against all other nodes in the graph. This gives us a starting point to eliminate edges. 2
Let's discuss the full SIMPLE algorithm. This algorithm works as follows. We start with a subset 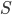 of all nodes: the seed set. We also define the set of all potential edges
of all nodes: the seed set. We also define the set of all potential edges 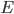 , which initially consists of all node pairs
, which initially consists of all node pairs  for all distinct
for all distinct  .
.
- For every seed
 and node
and node  , query
, query 
- If
 , there is no edge between node
, there is no edge between node 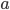 and
and 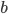 . We remove
. We remove  from the set of potential edges
from the set of potential edges 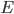 .
.
- If
- For all potential edges
 in
in 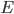 , query
, query  .
.
After step 2, we are done and we found all edges! We start with querying all nodes with a small set of nodes. If this is not too large, it only costs us  queries. Then, in step 2 of the algorithm we still do
queries. Then, in step 2 of the algorithm we still do  queries extra, to check all potential edges that we did not eliminate yet.
queries extra, to check all potential edges that we did not eliminate yet.
The proof that this set  is small is not easy, so I will skip that here. The authors of the SIMPLE algorithm show that this algorithm can find all edges in a graph with
is small is not easy, so I will skip that here. The authors of the SIMPLE algorithm show that this algorithm can find all edges in a graph with  queries, and that it works for all general, bounded-degree graphs.
queries, and that it works for all general, bounded-degree graphs.
When me and my colleague heard of this algorithm, we were wondering whether it could work even better for special types of graphs. In specific, we checked out geometric random graphs, where nodes have a position and edges only exist between nodes that are a distance less than 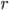 apart. Almost every real-world network has an underlying geometry: the internet network routers are located in the world; in a social network, your friends often live close to where you live and a train network connects cities that are close to each other.
apart. Almost every real-world network has an underlying geometry: the internet network routers are located in the world; in a social network, your friends often live close to where you live and a train network connects cities that are close to each other.
Our idea was that this should allow for faster reconstruction as you have more knowledge on the edges: there will not be edges between nodes that are far apart.

An example of a geometric graph
We found out that this geometry indeed causes a faster reconstruction time! We can decrease the number of queries because we can eliminate even more potential edges in the geometric graph, because we know that edges can only exist if the distance between two nodes is less than 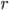 .
.
To prove this (or at least give some intuition), we have to introduce another distance. We already discussed the shortest path distance, but we now also use the Euclidean distance, which we denote by  . The Euclidean distance is the straight-line distance between two points - also called `as the crow flies'. If you could fly directly to a location in a straight line, without following roads or paths, the length of that line is the Euclidean distance.
. The Euclidean distance is the straight-line distance between two points - also called `as the crow flies'. If you could fly directly to a location in a straight line, without following roads or paths, the length of that line is the Euclidean distance.
If we know that the shortest path distance  , we know because of the geometric graph that these nodes have an Euclidean distance of at most
, we know because of the geometric graph that these nodes have an Euclidean distance of at most  apart in Euclidean distance. Dani et al.3 also found a lower bound: if
apart in Euclidean distance. Dani et al.3 also found a lower bound: if  then
then  .
.
Using these bounds, we can then find an approximate location of every node after we did some querying. This means that we can eliminate even more potential edges, as we know that nodes that are far apart will not have an edge. Therefore, there are relatively few potential edges, as those can only happen locally. And that is why we can efficiently reconstruct geometric random graphs!
- Mathieu, Claire, and Hang Zhou. "A simple algorithm for graph reconstruction." Random Structures & Algorithms 63.2 (2023): 512-532.\\ ↩︎
- By using simulations, I found out that in the geometric random graph, only 4 seeds - one in every corner - is enough to reconstruct the entire graph very efficiently! This works because these 4 strategically chosen seeds maximize the number of potential edges we can already eliminate because the difference in graph distance to two nodes is larger than 1. ↩︎
- Dani, Varsha, et al. "Reconstruction of random geometric graphs: Breaking the
 distortion barrier." European Journal of Combinatorics 121 (2024): 103842. ↩︎
distortion barrier." European Journal of Combinatorics 121 (2024): 103842. ↩︎