Have you ever found yourself less popular when compared to your friends?
Do you think you have more friends than most of the people in your friendship group? Then you probably feel popular. You are less likely to feel that way if you are isolated. Or if you believe that you have fewer, or at most an equal number of friends than your friends have.
Interestingly, in any group of individuals, on average, people have fewer friends than their friends do, or at the very most, an equal number. Not more! This dynamic between the number of friends you have, compared to the number of friends your friends have, is called the friendship paradox. This statement has a mathematical proof. It was first proved in 1991 by Scott L. Field, an American sociologist.
This fascinating phenomenon can, at first glance, only make us feel either happy or disappointed. However, it has many other perspectives to discover.
Since the friendship paradox addresses the average feeling within a friendship group, the primary question is: are the majority of us less popular than our friends? If most of us find that our friends are more popular, we might be inclined to imitate their behaviour. Could this lead to systematic biases in perceptions and social norms? From a political perspective, could it influence party voting results?
In fact, the friendship paradox extends beyond a mere statement. Delving into its deeper layers can offer valuable insights into social dynamics and their influence on our world. This story aims to uncover these insights concisely.
Formal description
In mutual friendship, if you are friends with someone, that person is also friends with you. This means both people consider each other friends.
Each friendship group with mutual friendship relations can be represented by a graph, known as the friendship network. In this graph, each individual is a point of the graph and the friendship between two individuals is a line between their corresponding points. If you take the characters of your favorite movie or show and connect them based on their friendships and alliances then you obtain their friendship network, for example like the one below for the characters of Game of Thrones.
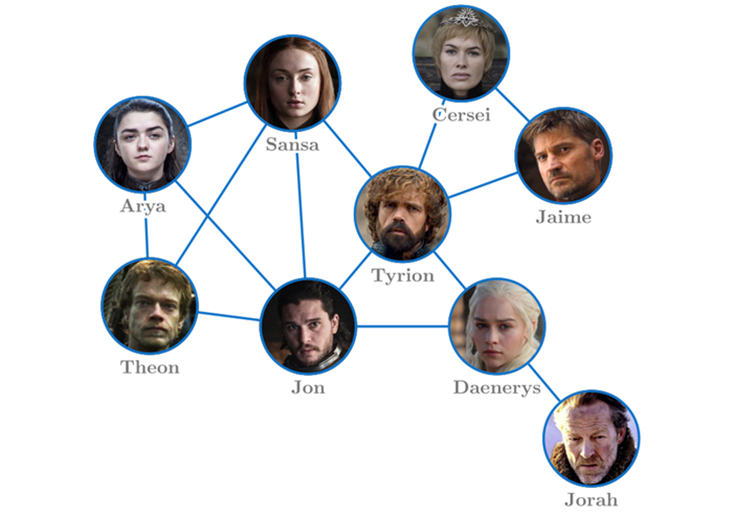
Two numbers that are important if we want to understand the friendship paradox are the average number of friends of the friends of a person, and the number of friends of that person. To see how it works in practice we will calculate both numbers in the friendship network from Game of Thrones.
Person
No of Friends
No of Friends of Friends
Average No of Friends of Friends
Arya
3
Theon
3
Sansa
4
Jon
5
Tyrion
5
Cersei
2
Jaime
2
Daenerys
3
Jorah
1
Let us calculate the difference between the average number of friends of the friends of a person and the number of friends of the person. We will call it the friendship bias of that person.
Person
Friendship Bias
Arya
Theon
Sansa
Jon
Tyrion
Cersei
Jaime
Daenerys
Jorah
Can you see which individuals could have a high friendship bias? And which would have one close to 0 or negative? Individuals who have a few friends who have many many friends will typically have a high friendship bias (their friends are very popular), while individuals with many friends who don’t have many friends will typically have a low friendship bias.
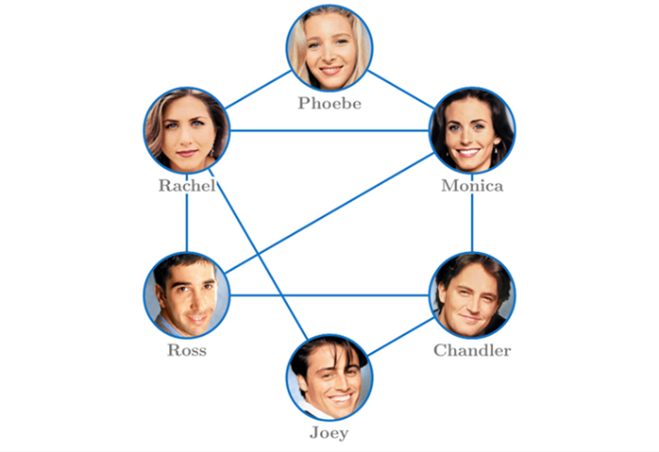
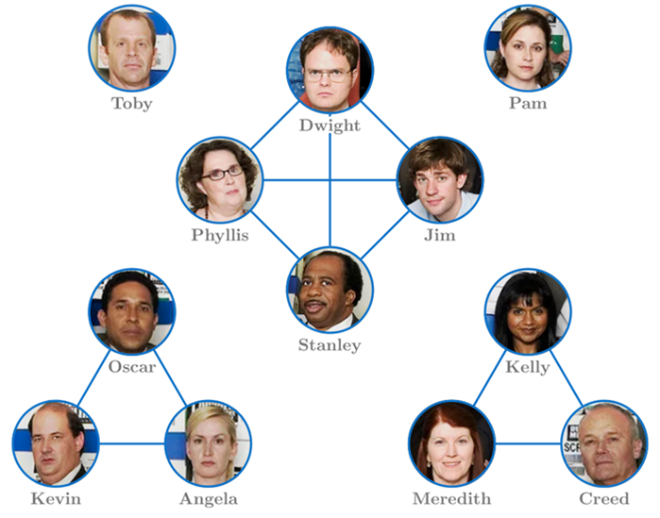
What do we learn from this computation? We see that a high value of someone’s friendship bias means that their friends are on average more popular than themselves. Since this is just on average it could mean that there is one friend who is much more popular, or that all of them are a little bit more popular. A negative friendship bias means that they themselves are on average more popular than their friends. But here comes the surprising highlight! By averaging the friendship biases of all individuals in any friendship network, we always obtain a non-negative value! We refer to this value as the average friendship bias. For the Game of Thrones network above the average friendship bias is . Can you compute the friendship bias for the friendship networks from Friends (two people are connected if they have been roommates) and the Office (people of the same department are connected)?
Is it really a paradox?
Although the friendship paradox is famous as a paradox, it is a hard fact! Let us see an example to gain some intuition why this is true. If you have 100 friends in a friendship network and each of them has fewer friends than you do, you contribute to increasing the friendship bias for each of those 100 people. In contrast, if you have one friend, you can only decrease the friendship bias for that one person. Why is this? (Look at the definition of the friendship bias). These interactions between the number of friends of highly-connected people and low-connected people produce this non-negativity of the average friendship bias.
You can play around with the GoT, Friends, and the Office-friendship networks, remove some connections or people from the network and compute the average friendship bias of the new network you obtain. By experimenting with examples on your own, you will understand beter how this delicate balance between highly-connected and low-connected people affects the friendship bias. But you will see that it always stays non-negative. This fact about networks can also be proved mathematically using concepts from the field of graph theory.
Most people in a group les popular than their friends?
You might imagine a group of people where many have more friends than their friends do. So far, we have discussed that the average friendship bias among individuals in a group is always non-negative. However, this does not mean that everyone has a non-negative friendship bias. We have also seen this in the examples, some people may have a negative friendship bias. Those who are more popular than their friends.
You may now wonder, since the friendship bias is always non-negative, could it be that most people in the group are less popular than their friends? If not, then more than half are more popular than their friends. Despite this, the friendship paradox still holds true for that network: on average, people are less popular than their friends.
Actually, the number of people with a non-negative friendship bias is NOT always greater than or equal to those with a negative friendship bias. In some networks, it can be significantly fewer. Imagine a roundtable with 11 people where everyone is friends except for two individuals who are not friends. In this scenario, only 2 individuals have a positive friendship bias, while 9 have a negative friendship bias. Yet, the friendship paradox still holds true!
This example can even be extended to a larger group, with the same result: 2 individuals with a positive friendship bias and the rest with a negative friendship bias.
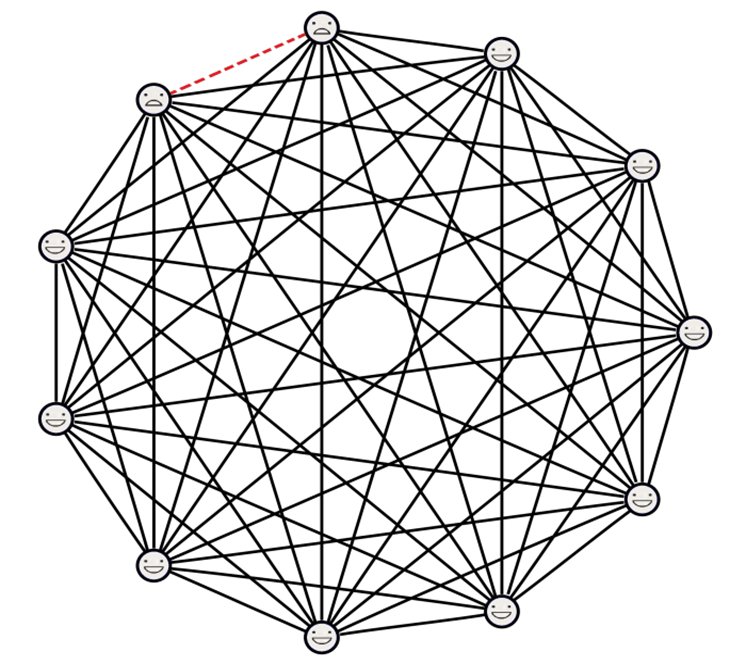
In this network, only two people have a positive friendship bias, and the other 11 all have a negative friendship bias. However the average friendship bias is still positive!
Evolution of friendship
Now, consider another scenario that is more relevant to us: a friendship network that starts with one person. Over time, additional people join the network one by one. These new people choose to connect with some person already in the network. Each new person prefers to connect, start conversations and form friendships with those who have more friends at that time. They may also become friends with less connected people, but with a lower chance. Such mechanisms arise typically in the evolution of social networks, where people with many connections (friends or followers) are more likely to attract the attention of new people joining.
This mechanism is referred to as the rich-get-richer model, where rich referred to individuals with a higher number of friends. Mathematicians have been studying this rich-get-richer mechanism by introducing a mathematical model called the preferential attachment model. In this model, points are being added to the network over time, and they are more probable to connect to points with many connections. The randomness in this network arises from the fact that newcomers do not have a predetermined choice of whom they will befriend. In social media networks for example, as the number of people in the network increases, the network structure increasingly resembles the preferential attachment model. Below you can see an animation of how a network from the preferential attachment model is generated.
If we view the world as a friendship network, the pattern of friendships is quite similar to this scenario. In other words, individuals with more friends are more likely to acquire additional friends. Furthermore, due to the large number of people in the world, this friendship network can be effectively modelled by a large preferential attachment model. For the large preferential attachment model, we recently discovered that the number of non-popular individuals significantly exceeds the number of popular individuals.
How the friendship paradox creates a biased world?
Many of us tend to gravitate toward those we perceive as popular. We all belong to social groups where we interact regularly, even if we do not have friends there. This could be at school, work, the gym, and so on. These social groups make up our friendship networks.
Consider one of the friendship networks where we are less popular than our friends. Within this network, we typically identify one person as the most popular. Sometimes there are several popular individuals, but we naturally gravitate more toward one of them. Let us focus on that person.
This individual is likely well-connected, as they are more popular than us. This person might belong to a larger friendship network where they are also less popular compared to their friends. This pattern probably applies to their most popular friends as well, within an even larger network.
This pattern continues, eventually leading to the world friendship network. However, as we discussed, only a small fraction of individuals in the world friendship network are more popular than their friends.
Now, imagine if everyone started imitating the clothing style of their so-called popular friend. What would happen next? The entire world might end up wearing similar clothes to those worn by just popular individuals in the world friendship network. While this might be ideal for a major fashion brand, it could suppress creativity and reduce the richness of fashion diversity.
Even worse! Suppose the popular people in the world friendship network support violent action against certain groups or institutions. Imagine a situation where everyone begins to adopt the political ideologies of their most popular friend. The radical views could then become deeply rooted, potentially attracting more people. This can create a dangerous bias where extremist actions become more likely, and rational, moderate discourse is undermined.
It is no wonder that sometimes we see a behaviour spreading like an epidemic worldwide. There will always be individuals who try to act independently of their friends. However, if the imitation is done by a large enough number of people, we ultimately end up with a biased world that the friendship paradox is producing. And unfortunately, it is really the case!
If, after reading the title, your immediate response is to shout "1/6-th", then you have correctly answered the question. Well done! However, in this article we will focus on the meaning of this question. What exactly is this "chance" of which you've just exclaimed it equals 1/6-th?
We want our guts to be filled with a diverse range of mutually beneficial and competitive interactions, a perfect blend of friends, frenemies, and enemies to keep our guts active and body on its toes. Read how networks can help understand these interactions!
In this article, dear reader, I am going to show you in which way the development of your opinion during the last political issue, the spread of a virus among your acquaintances during the current pandemic, and the alignment of some particles lying inside the device from which you are reading this article are extremely comparable phenomena.
Common sense tells us that objects of comparable size should be equally hard to find. Yet, when searching inside a random network, surprises are awaiting . . .
. Can you compute the friendship bias for the friendship networks from Friends (two people are connected if they have been roommates) and the Office (people of the same department are connected)?
paradox
, it is a hard 
