Media created for the networkpages.nl
Algorithms
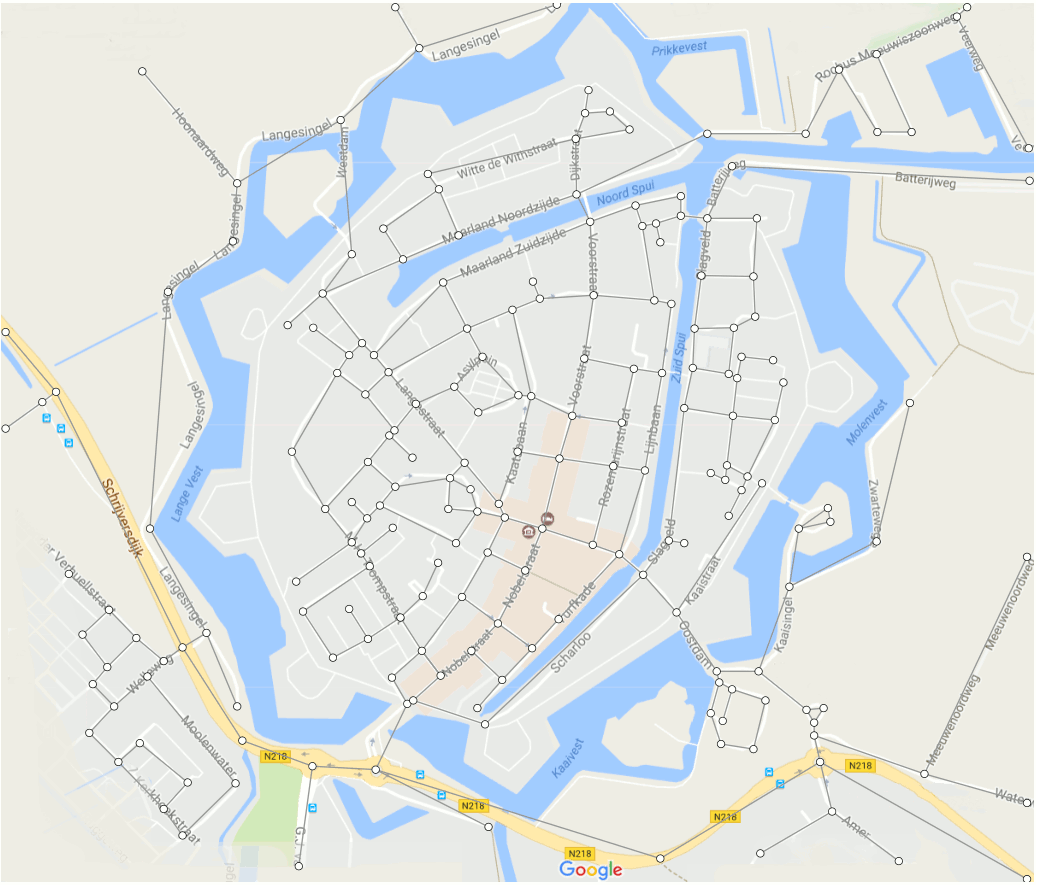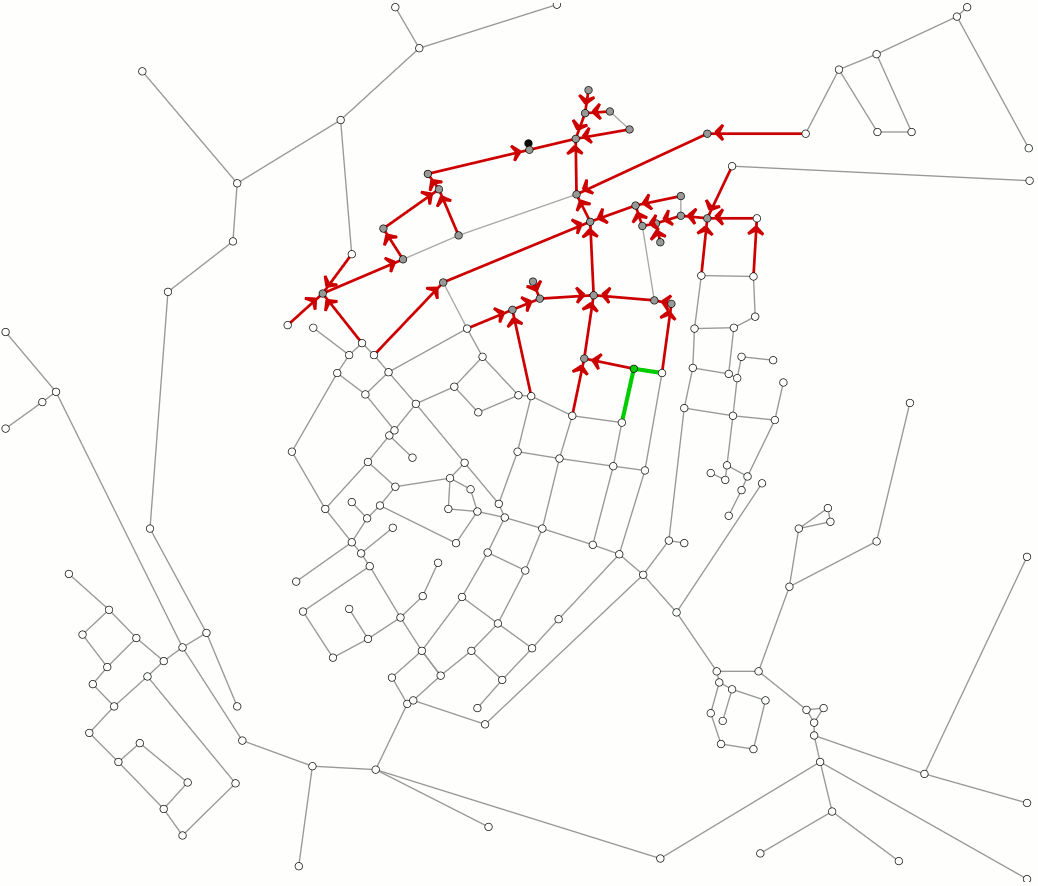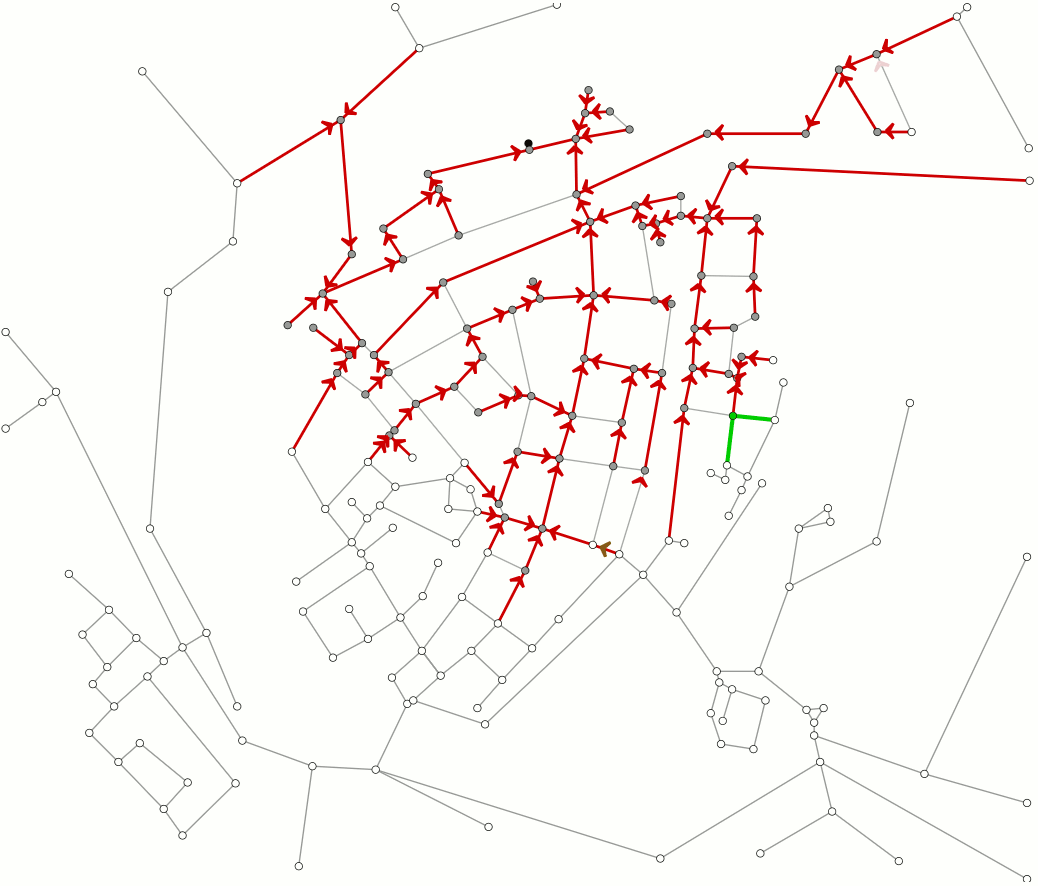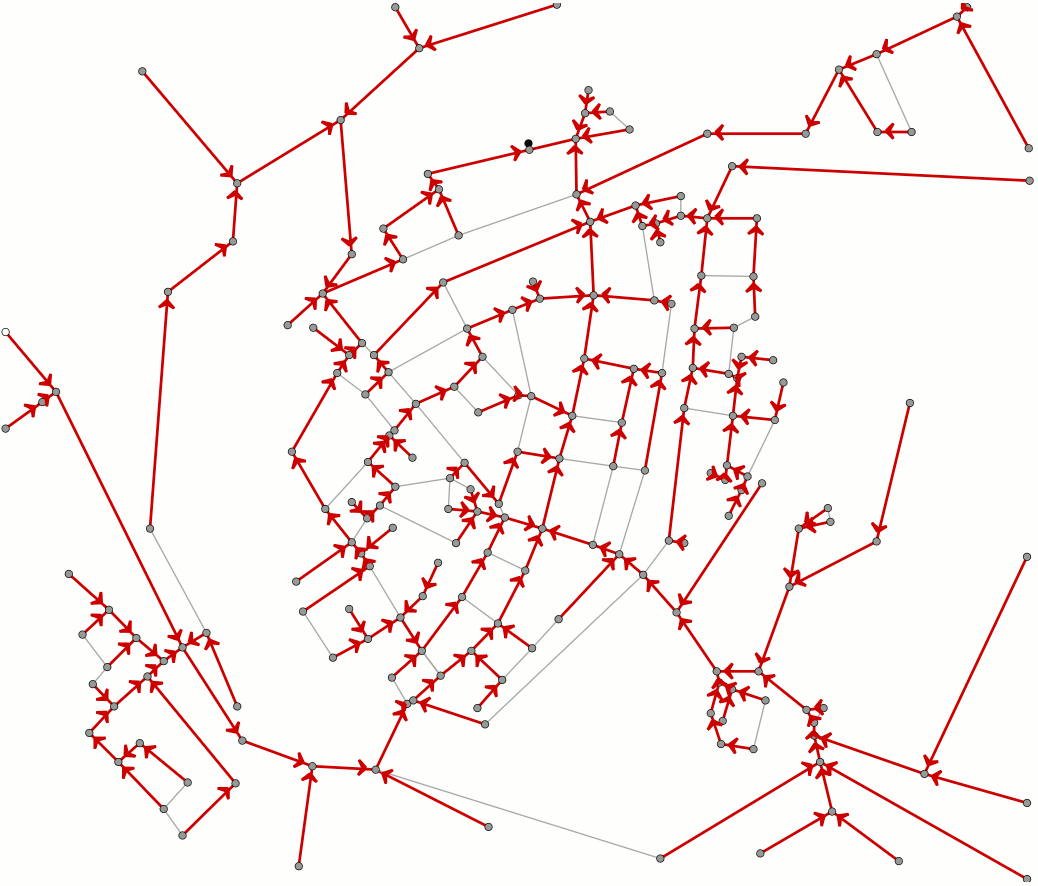
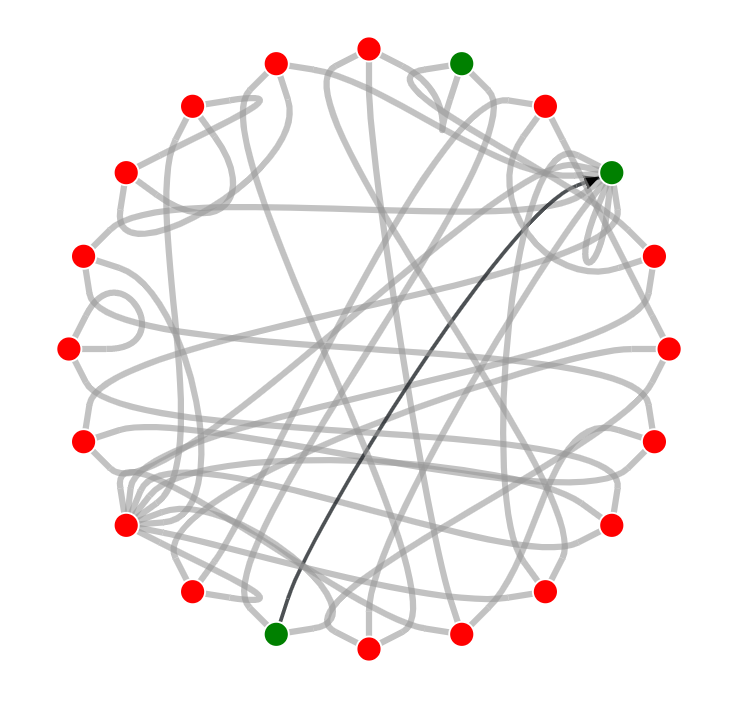
This animation shows how Dijkstra's algorithm works. This algorithm is used to compute the shortest paths between locations. As an example we use the streets of the Dutch town of Brielle. You can also read this article on Dijkstra's algorithm.
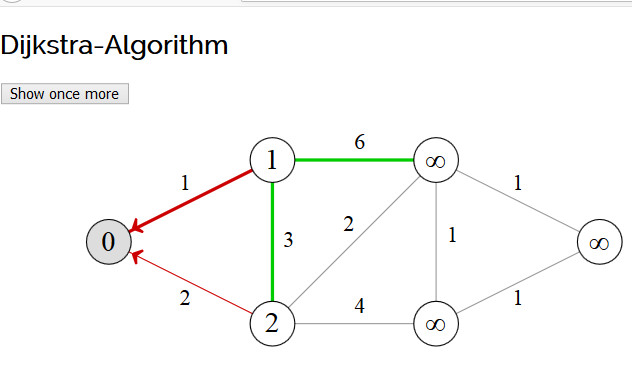
This animation shows in steps how Dijkstra's algorithm works, on a simple graph. You can also read this article on Dijkstra's algorithm.
- Simple trial and error to jump on top.
- Trial and error, but by using the best previous attempt as initial point.
- The program looks for solutions that require a small initial speed.
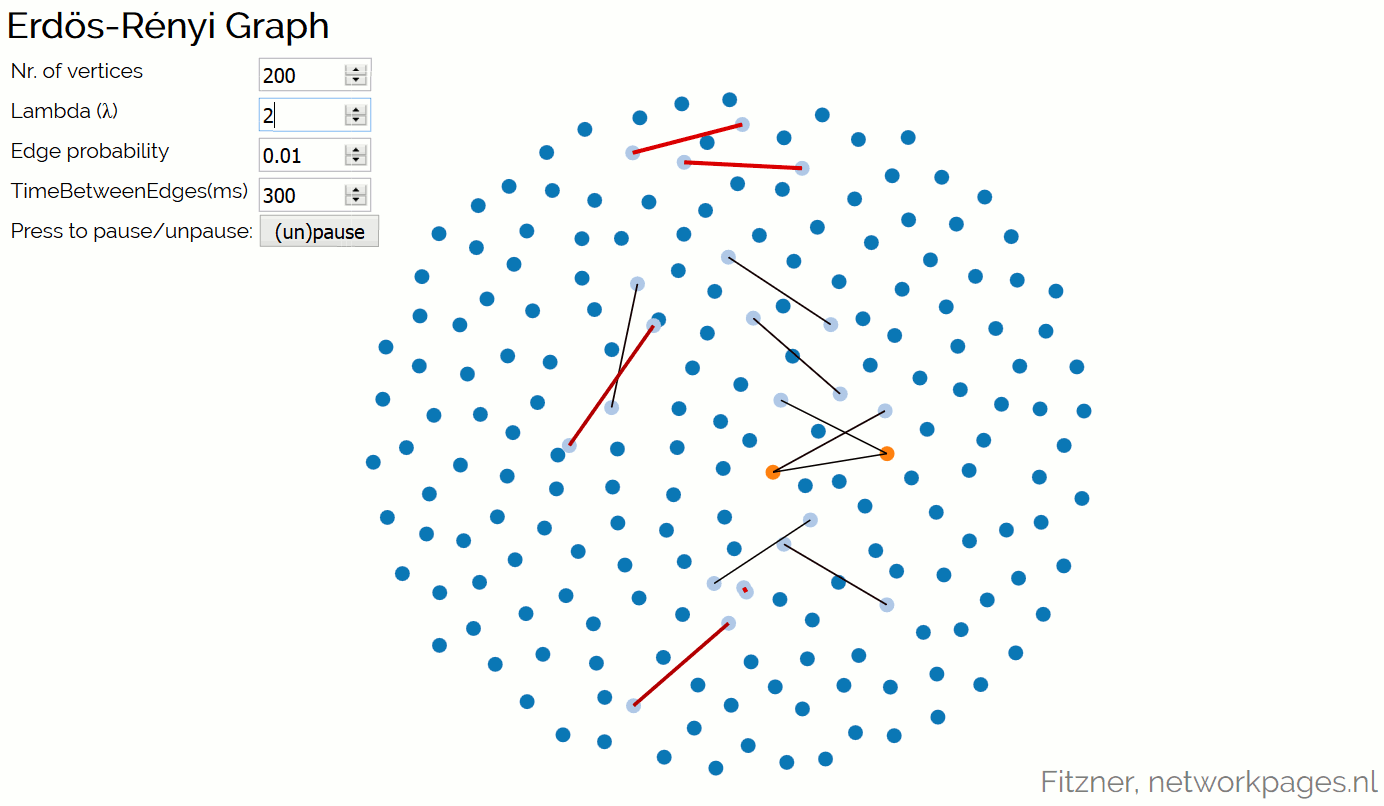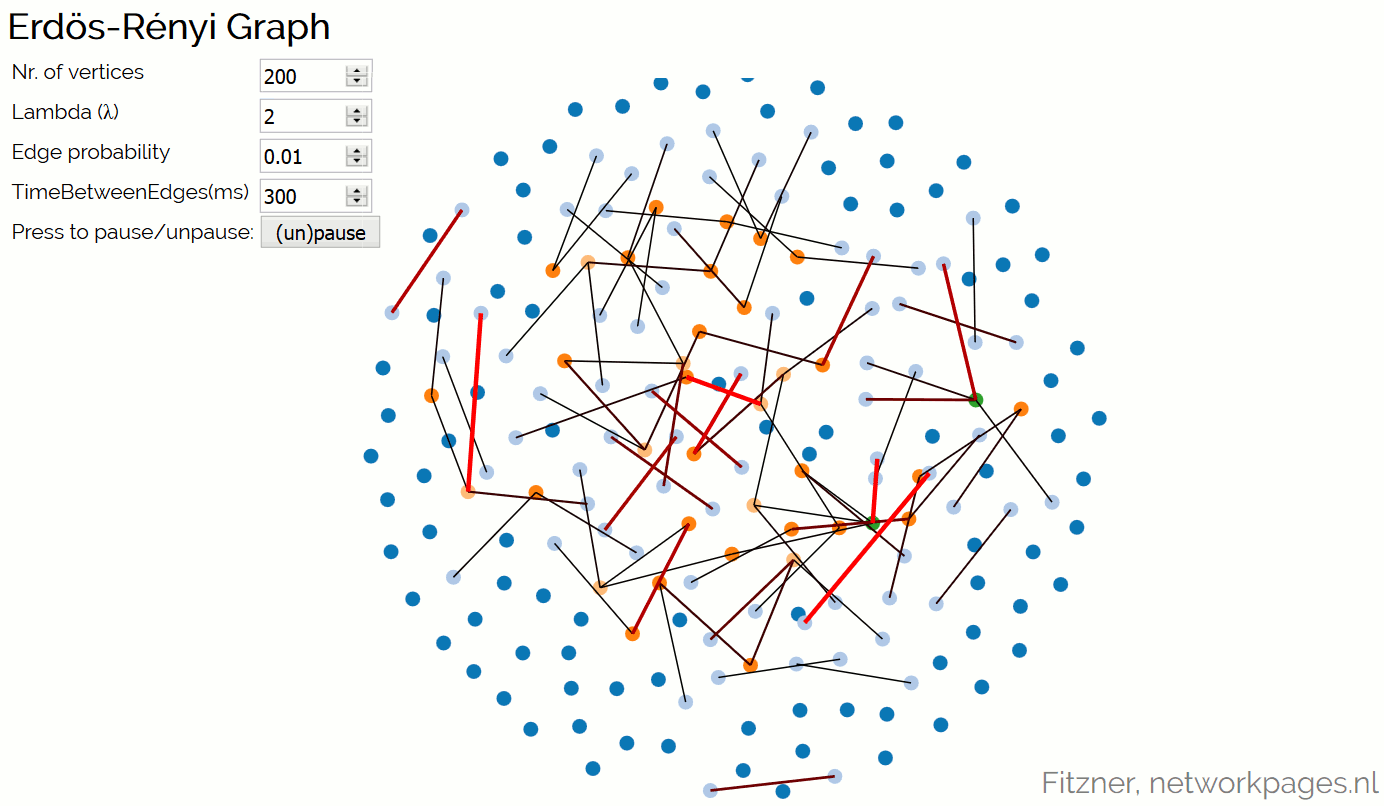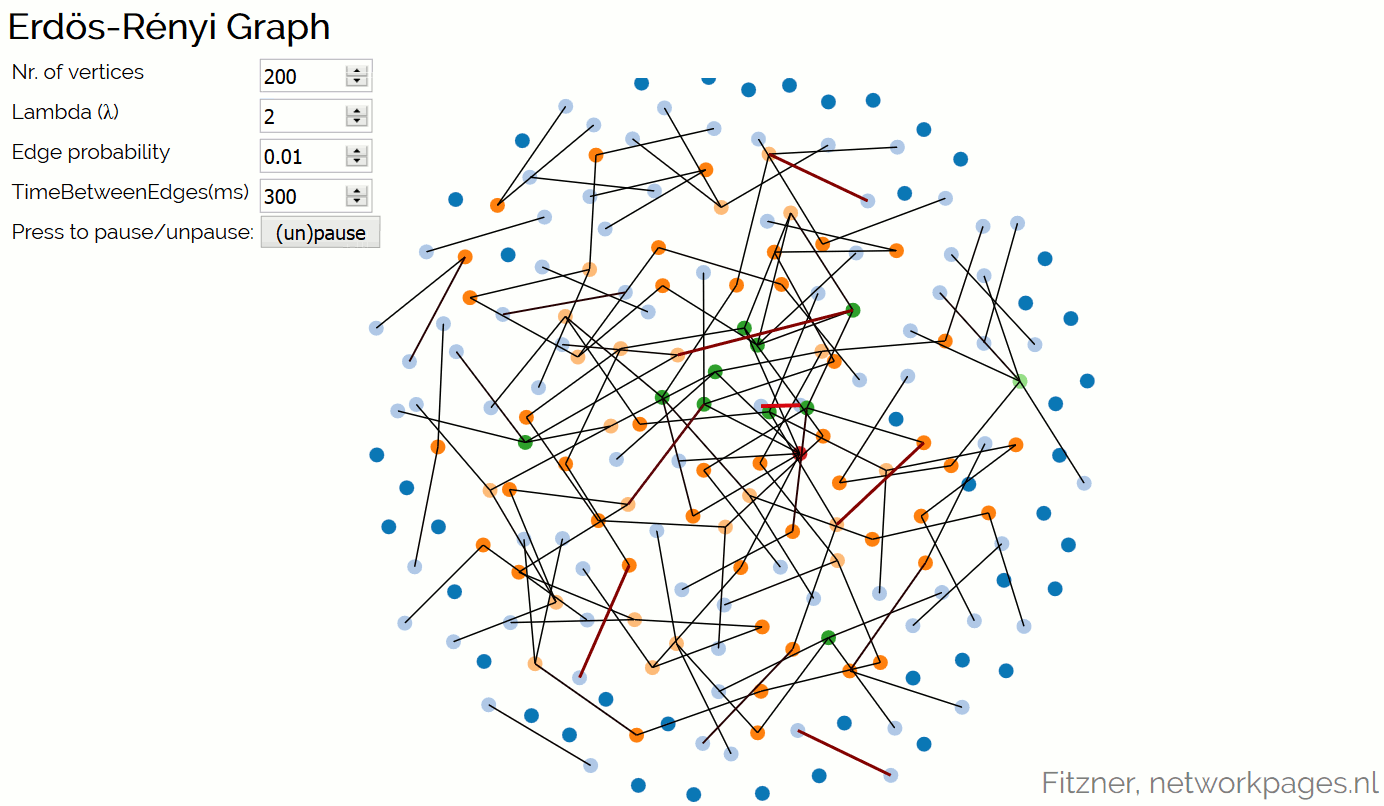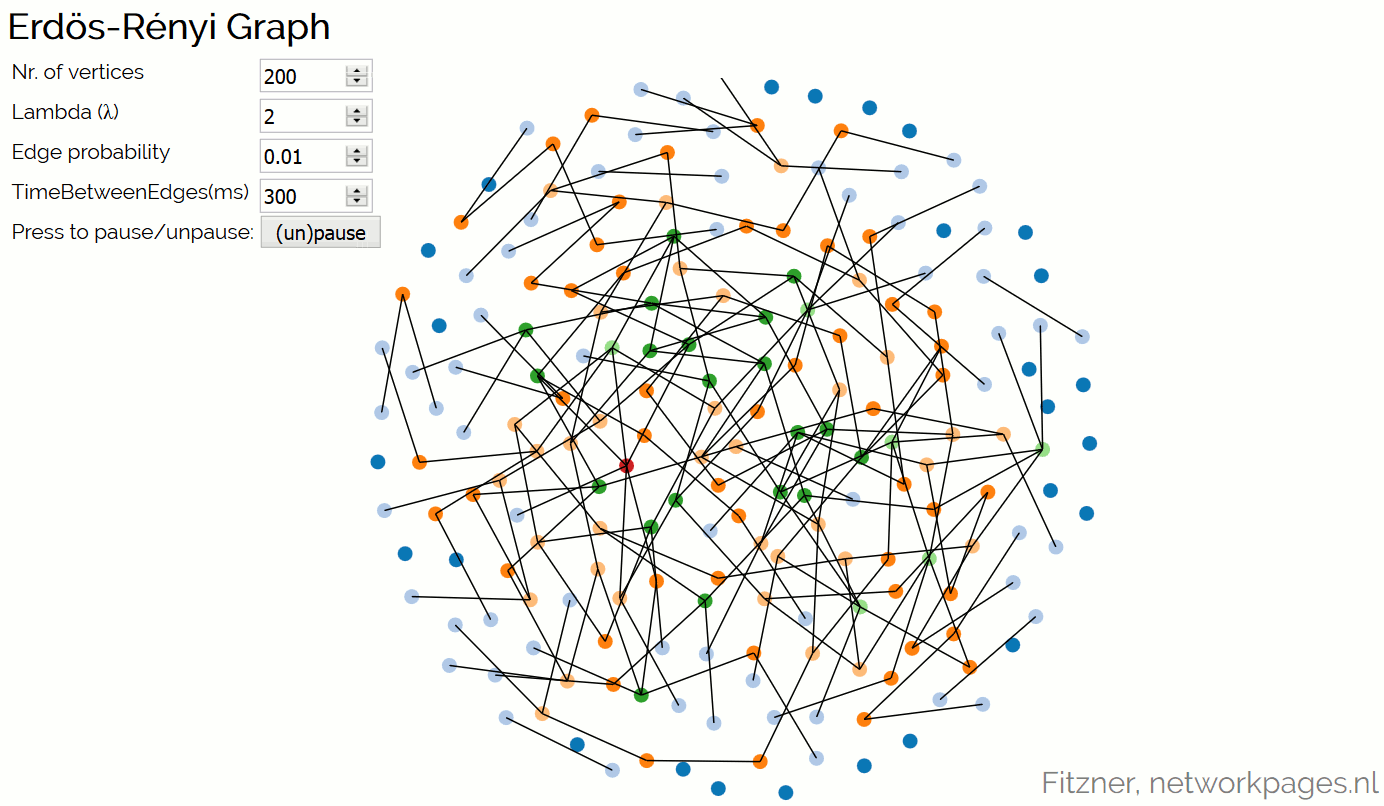
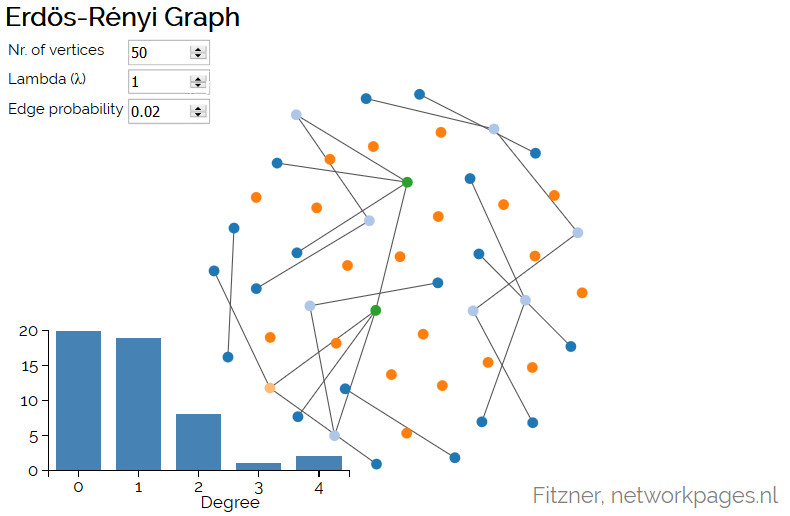
Erdős-Rényi Graph
Configuration model
Generates a graph from the Configuration model with the parameters given by the user. We also have an extension where we show a random walk on the resulting graph. Once the random walk starts, the color of the nodes indicates the local time. The aim it show mixing of the random walk.
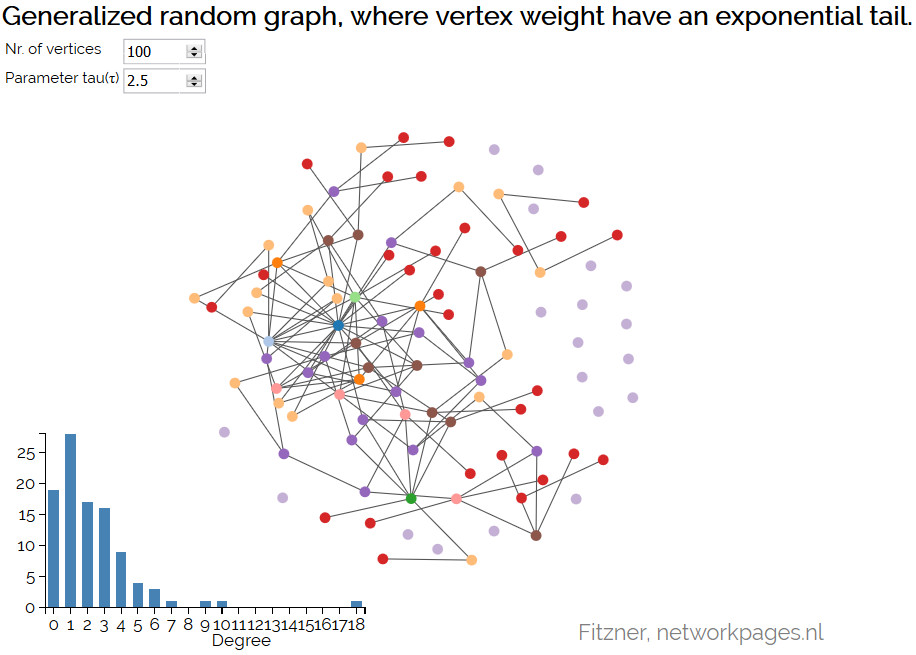
Inhomogeneous random graph
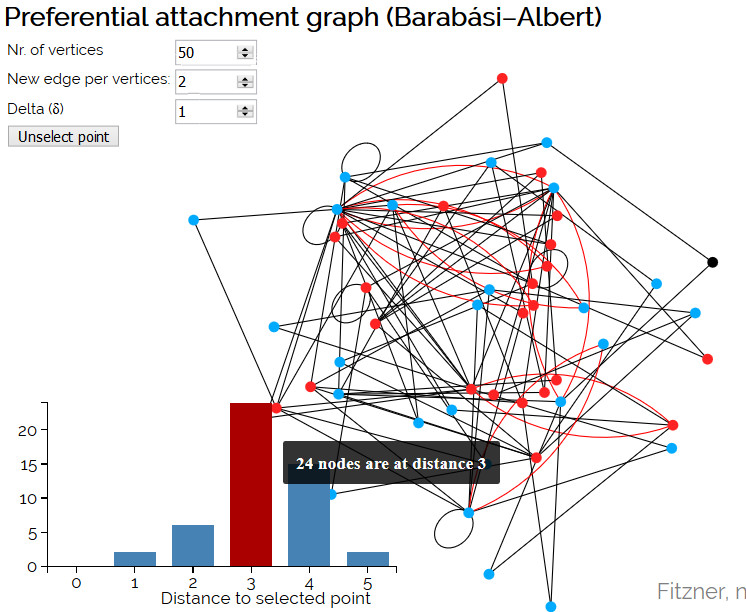
Preferential Attachment
Games
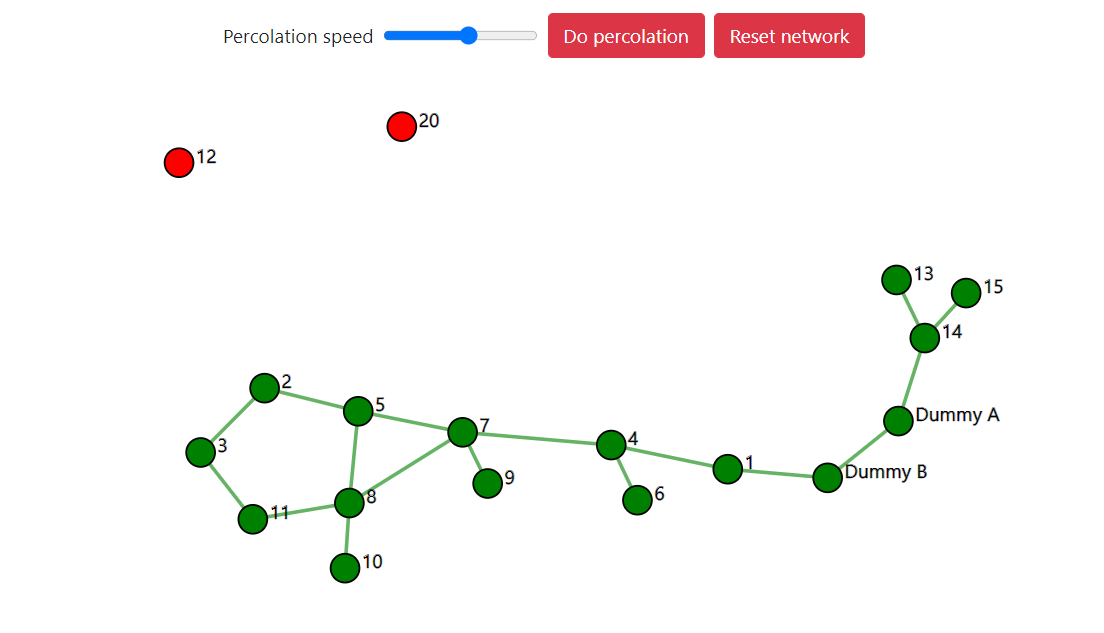
This Percolation game was made for a study day of the Dutch Association of Mathematics Teachers. Detailed instructions can be found here.
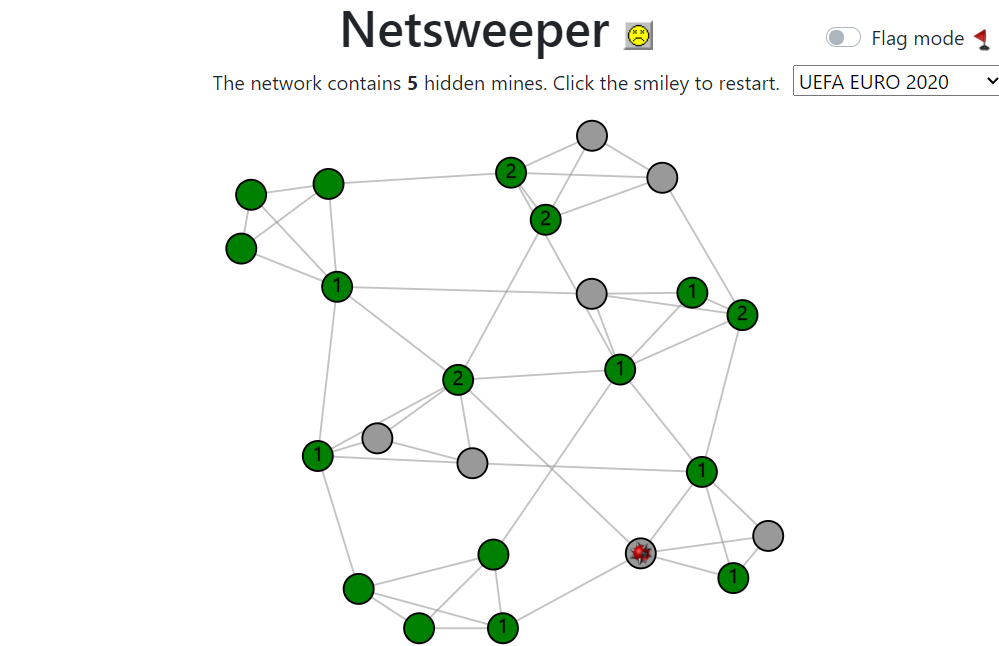
A variant of the classic Minesweeper game where the grid is replaced by an arbitrary network. The game is described in this article written by Martijn Gösgens.
Simulations
A simulation of a network with a community structure. In this simulation we generate a random network with communities and we show how an infection can spread on the nodes of the network.
Simulation of the two-community Kuramoto model for synchronization of the body clock. Used in this article by Janusz Meylahn.
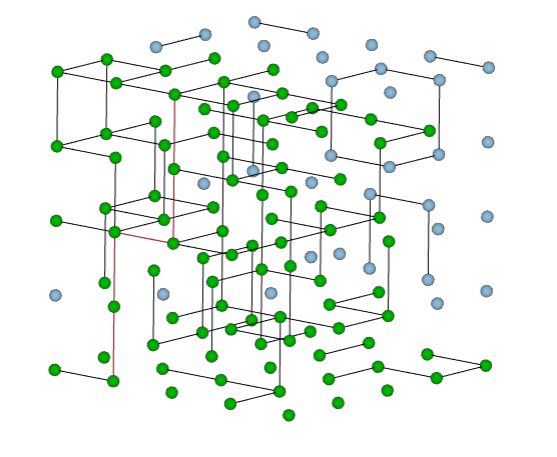
Simulation percolation on 3D grid. Used in this article by Nicos Starreveld.
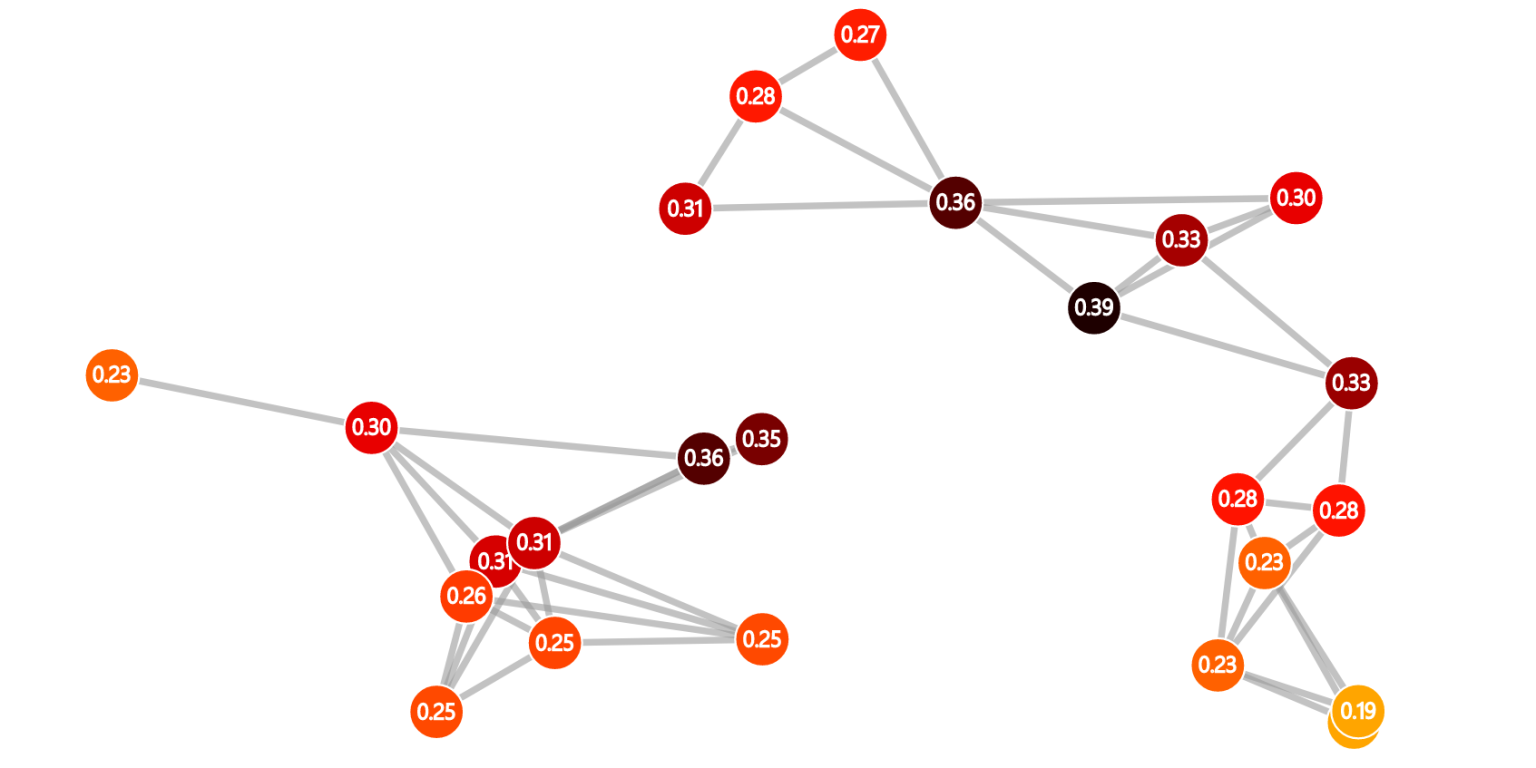
Simulation of removing the most central nodes in a graph. Used in this article by Manish Pandey.
In this simulation you can see which nodes are the most central given some centrality measure. You choose a graph generated from the Erdős-Rényi Random Graph, Preferential Attachment, Geometric, and Configuration Model. You can also choose a centality measure from Betweeness, PageRank, Closeness, Harmonic, Degree, Eigenvector, and Game of Thieves centrality.Simulation of a simple voter model on a CM network. The visualization also shows the network generation phase. Used in this article by Federico Capannoli. Several variations on other graphs:
Animation showing how Szemerédi's regularity result works. If you want to read more about this you can have a look at the article of Jop Briët.
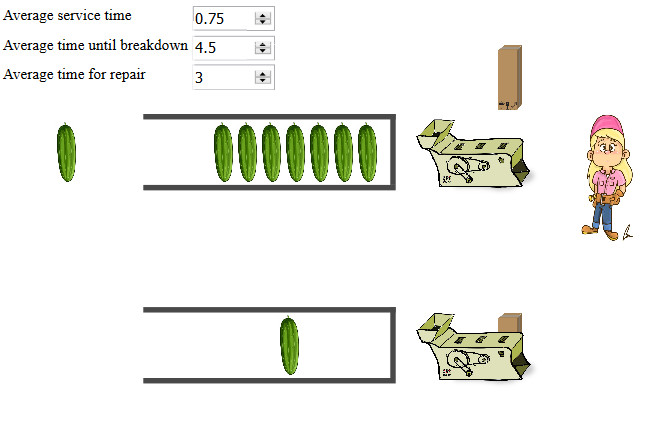
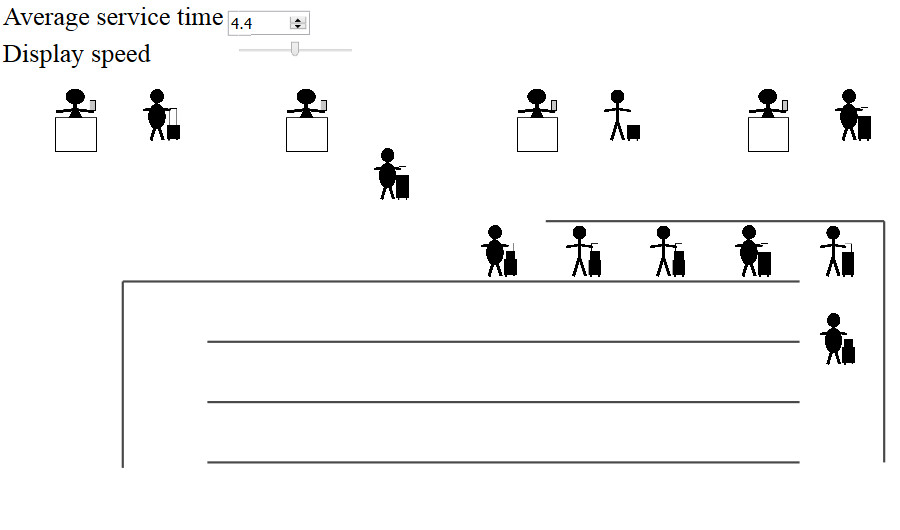
Queueing systems
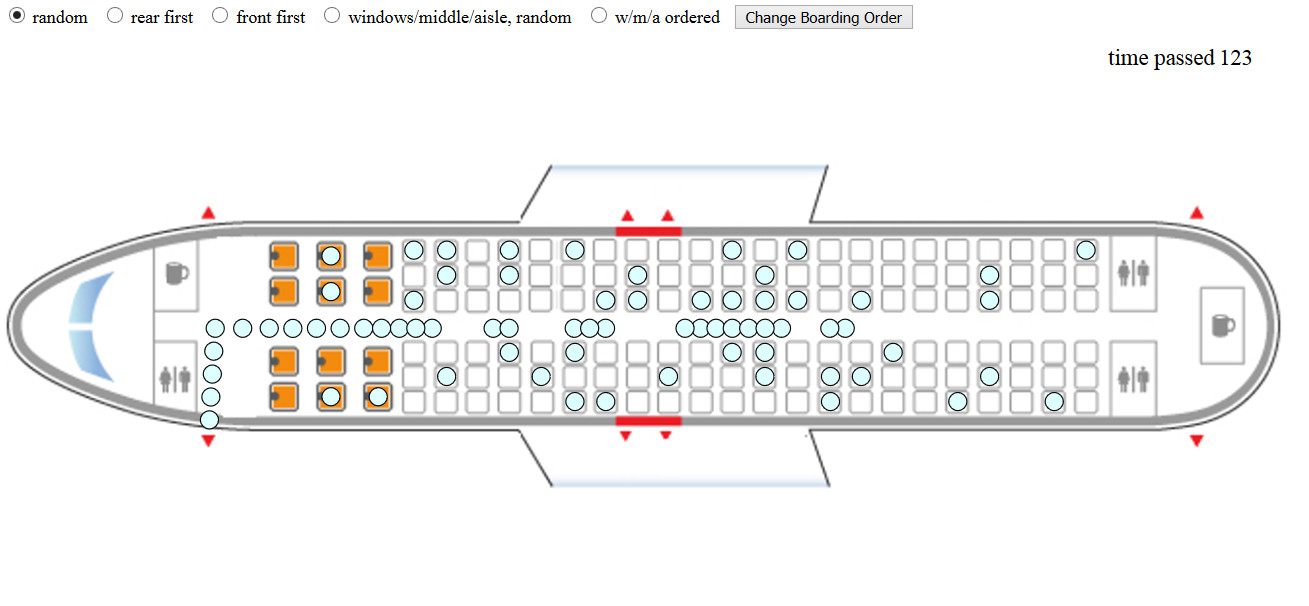
A simulation where you can try out boarding orders and see how they affect the total time it needs for all passengers to get on the plain. Do you think the best way could be implemented in an actual airport?
Infection spread and Vaccination
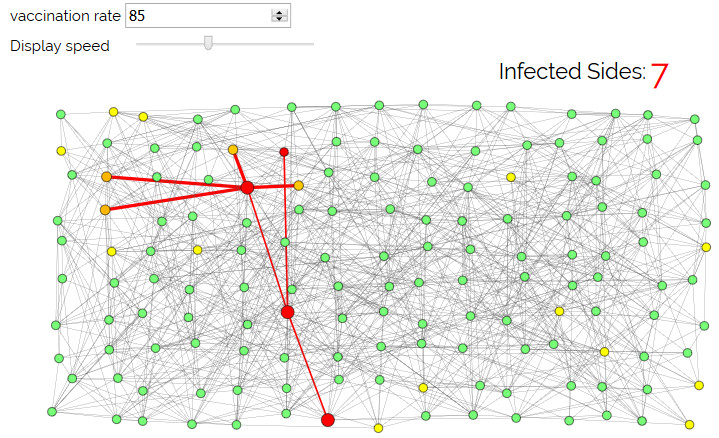
In this simulation we generate the connections of a random network shown on a grid. We show how an infection can spread on the nodes of the network.