Remember hearing: 'Please hold while you are connected to the next available agent'? Why not spend some of the time mathematical modeling saved you, on reading about it.
The use of phones is central in our everyday lives. Surprisingly though, as it was their original purpose, phones are hardly used to make calls anymore. People love the efficiency of multitasking, and being completely devoted to a conversation just is not that efficient, especially when the person you want to speak is not answering their phone.
Waiting is frustrating
We can all agree, a no. 1 source of frustration is the endless waiting on hold for a call center agent to pick up the phone (and no, listening to the annoying musical tunes while waiting doesn't soothe the torture). Interestingly, over the last 111 years mathematicians have been working on a vast theory to solve this call center inefficiency. Initially focusing on telephone exchanges, it was applied in call centers as soon as they popped up in the 80s. The theory is, as you will see if you read on, still highly relevant today.
The rise of contact centers
Call centers, probably due to widespread awareness of their infamous inefficiency and the inefficiency of making phone calls in general, are more and more a thing of the past. Nowadays, when you as a customer have a question for KLM about your (canceled) flight, you can resort to countless other options instead of dialing a phone number: KLM contact center can be reached through Twitter, Facebook, Instagram, WhatsApp and e-mail.
This development didn't quite solve the problem of waiting, unfortunately. In fact, it gave a whole new dimensionality to the problem, namely the distribution of employees over the different tasks (social media, e-mail, calls).
Job of manager
Imagine being the person in charge of this, the contact center manager. You need to make countless decisions, such as:
- How many employees with certain skills to hire?
- How to schedule them during the right (busy) period of the day?
- What task to assign them to?
Of course, you would totally stress out if you spot a team of idle employees waiting to answer phone calls, while a bunch of others try to cope with an overload of incoming questions through social media. There is no denying that the diversity in tasks brings new challenges. The good news is, the mathematics that has been developed for call centers have the potential to be applied in this setting too, with some adaptations.
Efficient customer care
Balancing between quantity of employees (who you have to pay) and quality for the customers (who pay you), the manager wants to keep everybody happy. To keep things simple, we will tackle the problem of efficiently managing call centers. It is useful to know how to answer this simpler question, before extending it to the case of contact centers:
How many agents do I need to immediately answer almost all of the incoming calls?
Mathematical modeling
When a call center is viewed through the eyes of a mathematician (or more specifically: a queueing theorist), it is put in the framework of service systems. Here competition is the driving force for efficiency. Customers enter service systems to compete for the scarcely available resources (which often comes down to handling time/service by an employee). At the same time, the service system (a.k.a. its manager), being in competition with rivals, strives for cost-efficient use of the resources. That is to say, queueing theory is a theory to avoid queues.
Many different models have been proposed to describe call centers. For these models performance measures as the average waiting time per customer and the average number of waiting customers, or the probability that a customer has to wait upon entrance can be computed. From the resulting expressions, a so-called desired service level can be attained by solving an inequality:
Find the minimum number of employees such that the performance measure is below a certain threshold.
As might not come as a surprise though, keeping in mind your own experience with call centers, mathematicians did not entirely solve the call center problem yet.
Golden rule
So, why is this not solved yet? To answer that question, we first have to look at the golden rule prescribed by mathematicians to determine the right number of employees. It is based on the so-called infinite-server approximation, which is a model where surprisingly no limit is set on the number of employee (meaning that no customer would ever have to wait). This approximation is useful because it allows us to apply a deep mathematical result, called asymptotic normality.
What we'd like to optimize here is the probability that the instantaneous load (which is related to number of open calls/requests) exceeds the capacity, which we can choose up to our liking. The instantaneous load is exactly the amount of time (in seconds) that it would take to handle all calls coming in that second. The capacity is the amount of work (in seconds) that can be done that second and is directly related to the number of employees to be assigned: the idea is that an average employee processes one second of work every second.
To compute the number of employees to be allocated using this rule, we just need to know two values: the average (instantaneous) load of the call center (we call this value '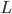') and the threshold we want to attain (we call this value ''). You can imagine that if the average load would be smaller than one, a single person could relatively easily handle the situation: on average, every second that goes by, he/she processes a second of work while at most another second of work comes in. Pretty balanced, right? Ideally, the number of employees handling calls is larger than or equal to the instantaneous load during every second of the day. However, it's not simple to attain this, most importantly because the instantaneous load is varying over time and subject to uncertainty, i.e., not known beforehand. The square-root staffing principle (aka the golden rule) aims to tackle the uncertainty using the concept 'hedge':
#employess = +.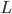
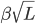The size of the hedge is a constant (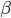) times the square root of the average load, hence the name of the rule. If the instantaneous load happens to be larger than the mean at times, the hedge will make sure that the extra load can be taken care of and no excessive waiting lines are formed. Imagine what would happen if we left out the hedge… The load would grow bigger and bigger without any sign of improvement, due to the slack of queueing callers.
Why a square root?
At this point you might have two questions. First, why is the hedge chosen in this way, or more specifically, what's the square root doing there? Second, where is the threshold mentioned before in this formula? Explaining what single observation underlies the square-root staffing principle will answer both these questions.
The relevant observation in fact is the previously mentioned result of asymptotic normality, which is stated in the famous central limit theorem (see this article by Jaap Storm for more on this). It describes the behavior of the sum of independent measurements of identical type, in the context of this article measurements on the instantaneous load. The central limit theorem tells us that the scaled sum of such measurements can be approximated by a standard Gaussian random variable, which is in turn described by the famous Bell curve.
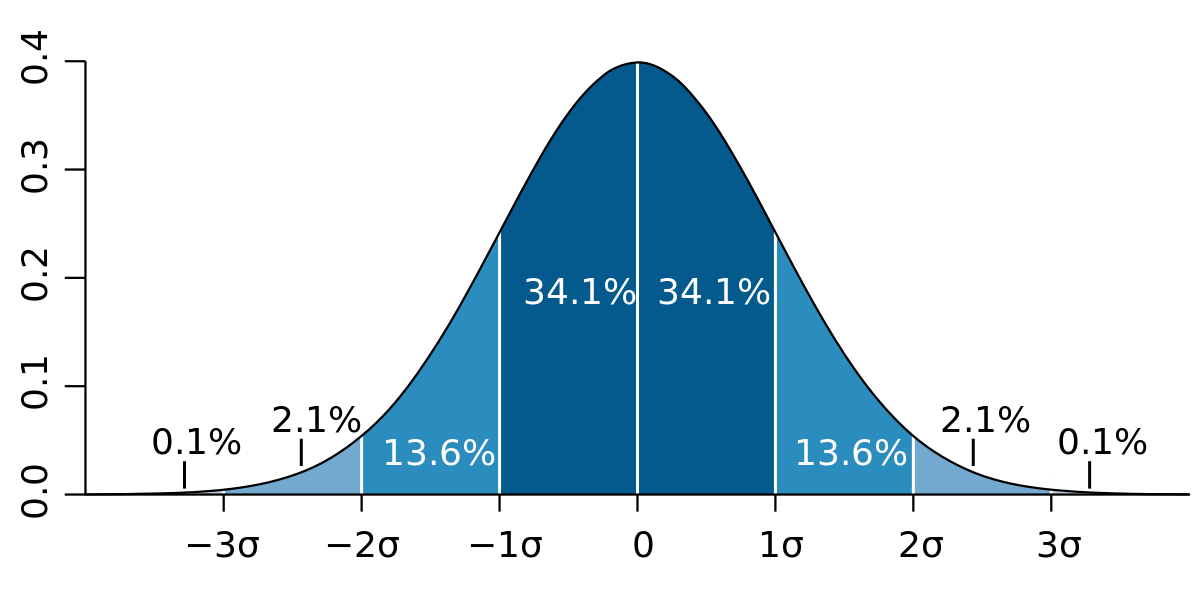
Figure 1: The bell-shaped curve of the normal distribution.
No memory
A standard assumption that mathematicians make about the stream of incoming calls is that the time between subsequent calls is uncertain in such a way that knowing that the last call arrived seconds ago gives absolutely no information about when the next one will show up (in comparison: when calls always enter 10 minutes apart, knowing gives the exact information on how long it takes until the next call arrives). This is called the memoryless property. It's reasonable to assume it holds because we often don't have any more information. Callers don't know about each other’s actions. Therefore, information on one caller's arrival does not guarantee anything on the arrival of the next.
This assumption is enough to ensure that the distribution of the instantaneous load approximately follows a bell curve, as this load can be seen as a sum of independent contributions (of identical type) of calls that arrived in the past and did not leave yet.
Consequently, it will look approximately like the curve in Figure 1, after shifting the curve of the instantaneous load by subtracting the mean load. Note that 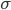in Figure 1 equals the square root of the variance (standard deviation). And as a matter of fact, in the classical theory the mean and variance of the load are assumed to be the same (both equal to 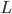), so the standard deviation is .
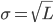Role of threshold
What does this mean? Well, suppose we set the capacity is set equal to 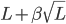(that is, more or less equal: we first round up to avoid split employees, as 2.5 employees unfortunately don't work faster than 2). Then from the Bell curve in Figure 1 we can extract the probability that the instantaneous load (on the 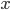-axis) is larger than what these employees can deal with right away (the capacity). We use that the surface under a specific section of the Bell curve represents the probability to end up in that section. For example, when 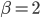the probability of `failure' is just 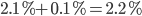(note that the Bell curve is centered, so 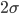in Figure 1 corresponds to a load of 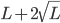. This is where the threshold reappears in the storyline. If we wish to only fail less than 0.1% of the time, then the correct choice for 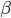is 3; the two values depend on each other through the Bell curve.
Example
Let's consider the example of a Q&A session at the end of an academic course. The idea is that students can visit the teacher's office to look into their corrected exam. Suppose a total of 100 students are expected to hop by between 10-12 AM and we have no specific information about their arrival times. On average it takes 6 minutes to answer all of one student's questions. The load is 6 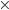100 / 120 = 5, which means that every minute we expect 5 'minutes of work' to arrive at the office. We conclude that it seems reasonable for the teacher to ask 4 of colleagues to assist him during the Q&A session, so that the 5 of them can handle all the incoming questions.
However, there might be periods where suddenly the office is crowded with newly arriving students and periods where no students arrive at all. This uncertainty makes it more complicated to decide whether 5 teachers can sufficiently complete this task in time. To keep students happy and maybe because of limited space in the office, we might want to ensure that no more than 1 out of 5 students has to wait before they can speak to a teacher/assistant. To guarantee this, we need some additional assistance: a hedge of order 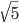, with 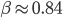, or: 1.88 = 2 extra assistants.
The square-root hedge will compensate for the uncertainty in the arrivals.
No waiting in the end?
Easy does it, a child could do the laundry as the Dutch would say. But it's not that simple. Although the memorylessness assumption and the infinite-server approximation are pretty defendable, there is a hidden assumption in the above which is tricky: we assume that at every moment in time, we must shift the curve with the same value 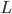for the average load. In practice, daily patterns in the load are observed, meaning that for example the load of callers in a call center is on average a lot lower in the morning than in the afternoon. Things get even worse, as the variance of the load in practice turns out way larger than the mean, rendering the 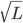incorrect.
The classical models for call centers were not realistic enough, which explains why we often had to wait on the phone when trying to reach a call center. As contact centers are getting more popular anyway, queueing theorists are currently focusing on how to extend the classical models available for call centers in order to save us valuable time waiting for a reply. The only valid reply to that: thank queue!
In 2014, in the Netherlands, Belgium and Germany, the average person spend approximately 40 hours in a traffic jam - that is 5 work days! In this article, I will explain how mathematical models with uncertainty help traffic engineers to make decisions that improve traffic.
average waiting time per customer
and the 
') and the threshold we want to attain (we call this value '
'). You can imagine that if the average load would be smaller than one, a single person could relatively easily handle the situation: on average, every second that goes by, he/she processes a second of work while at most another second of work comes in. Pretty balanced, right? Ideally, the number of employees handling calls is larger than or equal to the instantaneous load during every second of the day. However, it's not simple to attain this, most importantly because the instantaneous load is varying over time and subject to uncertainty, i.e., not known beforehand. The square-root staffing principle (aka the golden rule) aims to tackle the uncertainty using the concept 'hedge':
.
) times the square root of the average load, hence the name of the rule. If the instantaneous load happens to be larger than the mean at times, the hedge will make sure that the extra load can be taken care of and no excessive waiting lines are formed. Imagine what would happen if we left out the hedge… The load would grow bigger and bigger without any sign of improvement, due to the slack of queueing callers.
seconds ago gives absolutely no information about when the next one will show up (in comparison: when calls always enter 10 minutes apart, knowing 
in Figure 1 equals the square root of the variance (standard deviation). And as a matter of fact, in the classical theory the mean and variance of the load are assumed to be the same (both equal to 
.
(that is, more or less equal: we first round up to avoid split employees, as 2.5 employees unfortunately don't work faster than 2). Then from the Bell curve in Figure 1 we can extract the probability that the instantaneous load (on the 
the probability of `failure' is just 
(note that the Bell curve is centered, so 
in Figure 1 corresponds to a load of 
. This is where the threshold reappears in the storyline. If we wish to only fail less than 0.1% of the time, then the correct choice for 
100 / 120 = 5, which means that every minute we expect 5 'minutes of work' to arrive at the office. We conclude that it seems reasonable for the teacher to ask 4 of colleagues to assist him during the Q&A session, so that the 5 of them can handle all the incoming questions.
, with 
, or: 1.88 = 2 extra assistants.
incorrect.
