In this article, we have collected all the articles concerning algorithms and the mathematical theory of graphs. Enjoy!
In the first and the second part of our summer reads last week we collected some articles on the broad topic of technology and computation, and interviews and personal blog posts respectively. But there would be no Network Pages if we wouldn't pay attention to modern research into algorithms and graphs - a mathematical concept used to study networks.
Four colors to paint them all
A mathematician once told me that problems that are very simple to state can be very deceiving, and sometimes turn out to be extremely difficult to solve. One such problem was the Four Color Problem. In this article, we take you back to London, October of 1852, and into the scripts of mathematics student Francis Guthrie who was puzzling with this problem. A problem that would need more than a century to be solved!
A traveler trying to visit them all
If you want to read more about the Traveling Salesman Problem. Suppose you are running a delivery service. You have a single truck and each day you must deliver a large number of parcels to various cities throughout the country. Then you face the following problem: in which order should you visit the cities? In other words, you want to find a round-trip that starts at the depot where the parcels are kept, then visits each of the given cities, and finally returns to the depot. Such a round-trip is called a tour of the given cities. Of course, the goal is to find a tour with minimum travel cost. Here, travel cost can refer to the average time it takes to follow the tour, or the total length of the tour. Computer scientists call this problem the Travelling Salesman Problem, or TSP for short. You may think that if we know the cities to be visited and the travel costs of the roads connecting them, then a computer can easily compute a shortest tour. But the fact that TSP is so simple to state is deceptive: it turns out finding the best tour is extremely difficult, even with state-of-the-art computers. Want to know why? Readthis article.
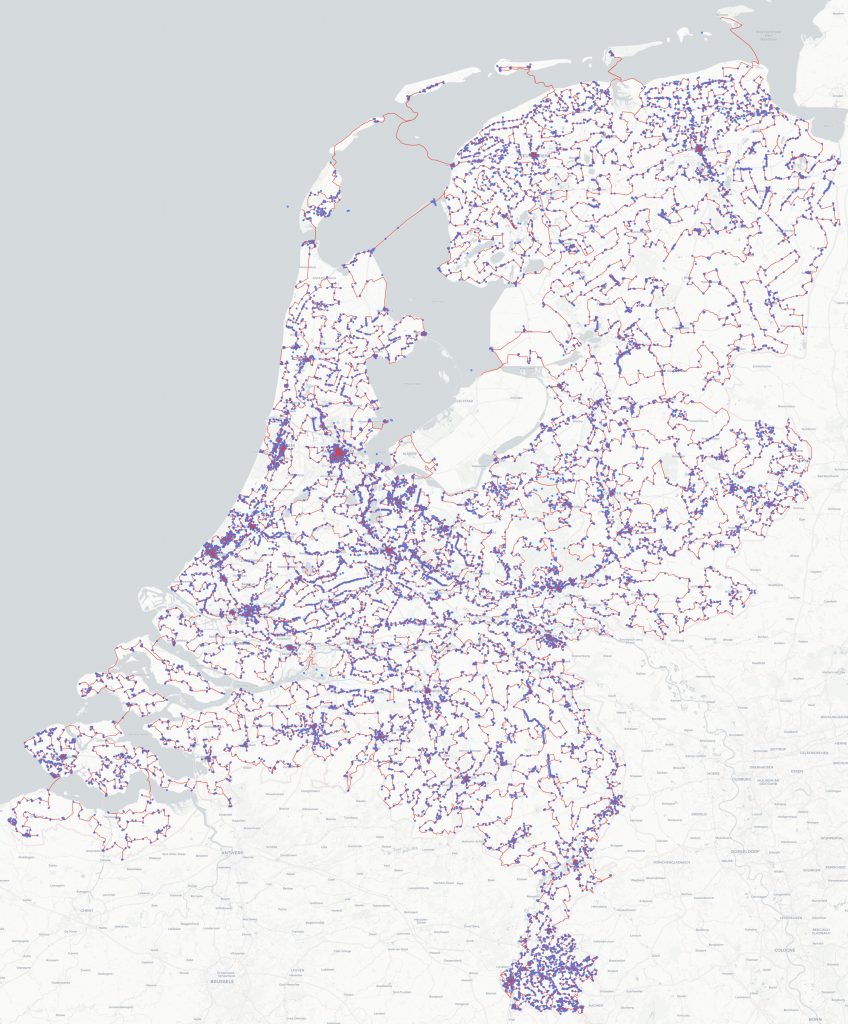
And if you want to read how the optimal tour between 57,912 national monuments in the Netherlands was computed, then you should have a look at this article!
Gossip, DNA and graphs
For those of you who want to learn about percolation theory and see a beautiful, but more abstract, result from mathematics you can have a look at this article.
Or maybe read how DNA-assembly is related to problems from graph theory? Then have a look atthis article!
Enigma: a complexity titan
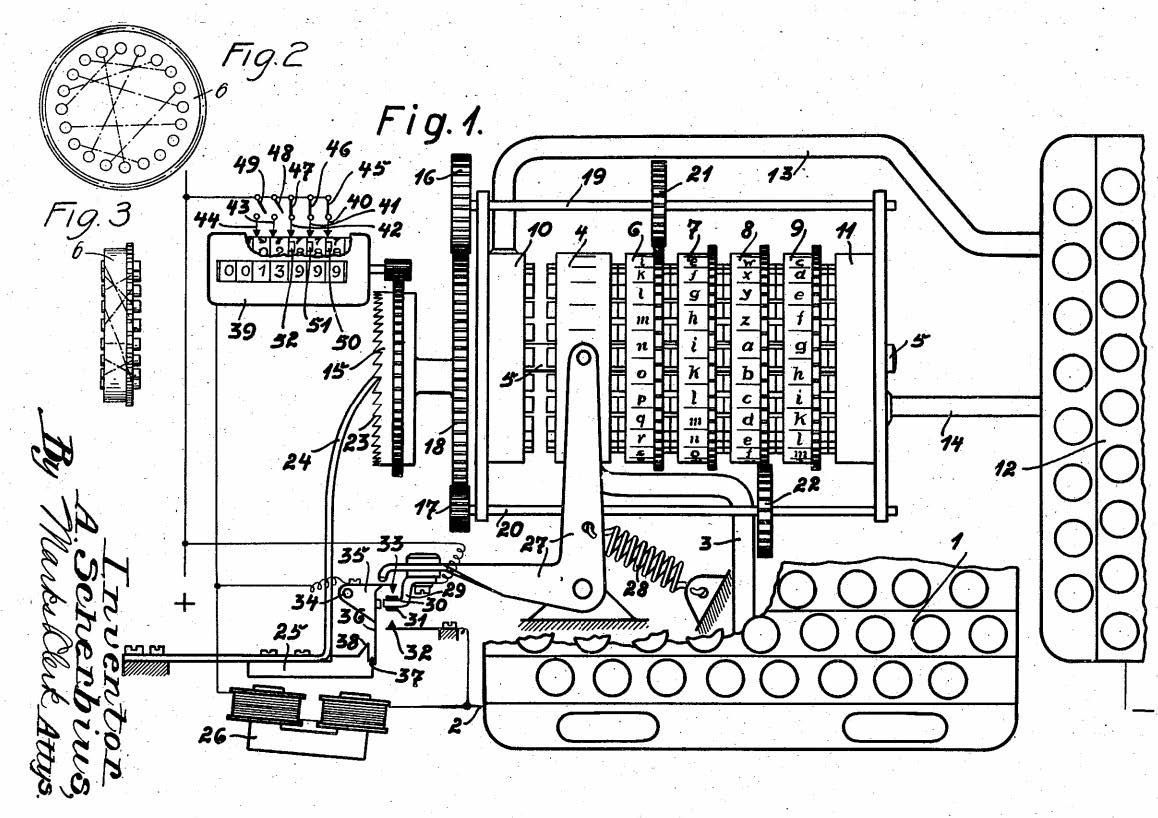
If you want to learn how the German encryption machine Enigma worked and how the British managed to crack it then have a look atthis article!
Next week the fourth and last part of our summer reads: articles on applications of mathematics in real-world problems!
Would you like to stay up to date whenever a new post appears on the Network Pages? Then subscribe to our mailing list, follow us on Twitter or on LinkedIn.
Last January I was very pleased to attend an annual summer school in discrete mathematics in Valparaíso, Chile. It was the very first time for me to attend such a summer school overseas as a master’s student. It was a wonderful journey, especially when discussing mathematics.
A conjecture of Erdős and Hajnal from 1989 says that forbidding any specific substructure results in existence of a very large homogeneous one! In this article you will have a look into one of the most fascinating problems in modern graph theory.
A mathematician once told me that problems that are very simple to state can be very deceiving, and sometimes turn out to be extremely difficult to solve. One such problem was the Four Color Problem.
Have you ever wondered how you can make mathematics interesting to the daily life of students? In this article, we will discuss two important and exciting concepts teachers can use to introduce graph theory in their classes.
