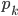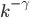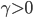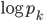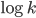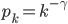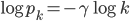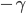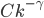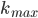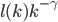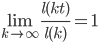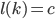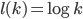In 2016 a company calculated that the average number of followers in Twitter was about 707. Although this might already sound like a lot, it pales in comparison with the top Twitter users. There are currently more than 100 users that have more than ten million followers. Some, like Barack Obama or Katy Perry, even have more than one hundred million followers, which is roughly 140.000 times larger than the average.
When the average number of connections in a network is not representative for the many large values we observe, network scientists call the network scale-free. This term reflects the fact that there is no typical scale. Many nodes have far more connections than the average suggests. The vast research on scale-free networks and their properties has helped make network science become the prominent research field it is today.
However, a cumulating lack of understanding and misconception among scientists regarding scale-free networks has led to confusion what scale-free networks are and if they are as omnipresent as earlier research suggested.
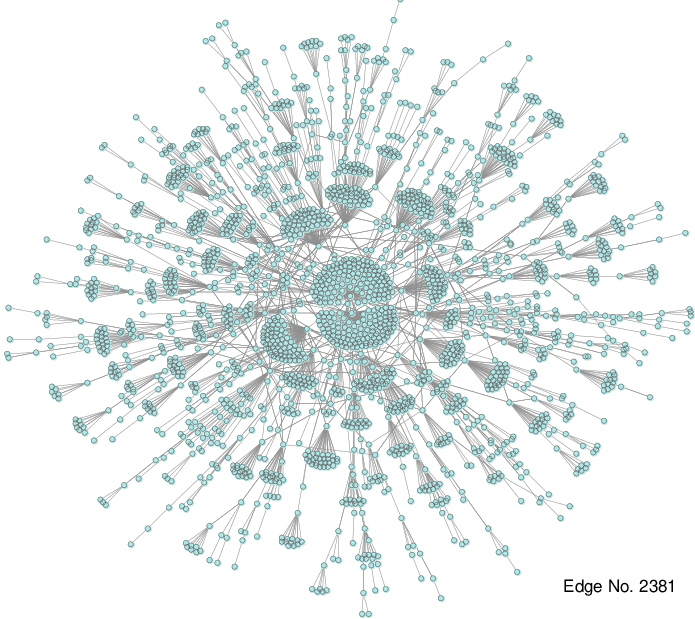
Visualisation of a scale free network
This problem is currently shaking the foundation of many branches of network science. Much research on networks has been based on the scale-free property. If most networks would turn out not to be scale-free then these results would end up in the garbage, setting network science back decades.
So what are scale-free networks exactly, what is the problem with them and most importantly, how can mathematics help resolve this?
Artistic visualization of a scale-free network.
No typical users in Twitter
Let us go back to the example of Twitter. This is a social network, a place where people interact and share information and opinions. When network scientists look at Twitter they also see a network, but in a more scientific way. For them a network is an abstract object made up of nodes and connections between them. In some cases these connections can be symmetric, like friendship relations. Other times they can have a direction. In the Twitter network, nodes are users and there is a directed link pointing from one user to another if the first user follows the second one. If you follow Barack Obama, then there is an link pointing from you to him. The number of followers a user has is called its degree. Users with many followers, such as Barack Obama and Katie Perry, have very large degrees and are called hubs.
The world around us is littered with many different types of networks. There are other social networks such as Facebook or Snapchat. Technological networks like the World Wide Web, consisting of webpages and hyperlinks. You probably used this network to find this article. Even the collection of intricately connected neurons that make up our brain form a network. Although these networks describe different systems, researchers have found that many of them contain hubs whose degree is several orders of magnitude larger than the average degree in the network. Think about how many friends/fans Katie Perry must have on Facebook or how many webpages have a link to the Wikipedia page of Stephen Hawking.
Why there are no real giants on earth
This extreme variety in the degrees of nodes is quite different from many other quantities we encounter in our everyday lives. For example, the tallest person in the world, Sultan Kosen, is 251cm. Although he might seem like a giant compared to the average Dutch male, whose height is 186cm, he is not even twice as tall. Imagine the heights of people would be like the number of followers in Twitter. Then the tallest person in the world would be approximately 260km!
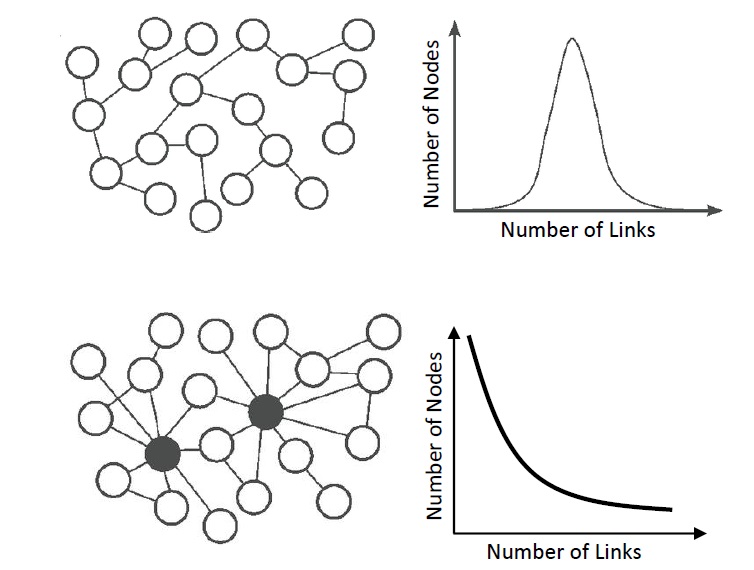
The absence of extremely large people can be observed mathematically, by looking at how the heights of people are distributed. Like many other every-day quantities, this distribution closely resembles what we call a normal distribution. This distribution is characterized by a symmetric curve, whose peak is at the average value and which quickly decreases when we move away from this value (see top picture on the left). The first part means that the height of most people will be very close to the average. The second part tells us that, although there are people that are reasonably smaller or larger than average, it is very unlikely to see values that are really far from the average. There are no giants among us.
Why there are giants in Twitter
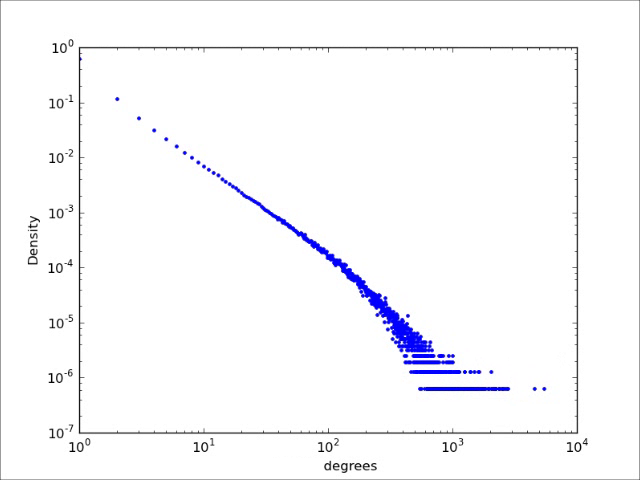
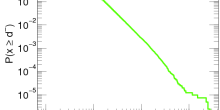
For the number of followers in Twitter the story is different. Researchers found that this distribution is not a normal distribution but exhibits a so-called power-law behavior. In fact, many other networks were found to have a degree distribution which resembles a power-law. Unlike the normal distribution, power-law type distributions are not centered around their mean and decrease much more slowly (see the bottom plot in the figure above). This increases significantly the probability to see, for example, users with a large number of followers or webpages with many links.
The number of followers in Twitter has a power-law behavior
How fast power-law distributions decrease can be characterized by a number, called the power-law exponent. This exponent is always greater than 2, and the larger it is, the quicker the distribution decreases. In other words, the larger the exponent, the smaller the variation in the degrees. An important situation occurs if the exponent is between 2 and 3. In this case the mean of the distribution is finite, but the variance is infinite. This means that although the average degree is some finite number, we are expected to see extremely large deviations from this value.
For Twitter the exponent is estimated to be around 2. This agrees with the existence of giants, like Barack Obama and Katie Parry, with more than one hundred million followers while the average number of followers is only 707. We must conclude that the average number of followers in Twitter is by no means a good indication for the number of followers we can expect to see. The existence of such extremely large deviation from the average degree implies that there is no typical scale for the degrees. That is why network scientist referred to such networks as scale-free networks.
In many networks, the fraction of nodes with degree seems to decrease approximately as an inverse power of . That is, if we denote by the fraction of nodes with degree , then is approximately , for some exponent . This type of behavior is referred to as a power-law. The existence of power-laws can be seen visually on a log-log plot, where we plot as a function of . If then and hence the log-log plot of resembles a straight line with a negative slope . These straight lines with negative slop on log-log scale is what many network scientist found when analyzing a great variety of networks between 1995 and 2002. In many cases, when they tried to fit a straight line to the data they found the slope (the exponent ) to be between 2 and 3. Such a log-log plot can be seen in the figure below.
Visualisation of a scale-free network
The power of the power-law exponent
The value of the power-law exponent has significant implications for the behavior of the network. For example, networks with exponent smaller than 4 are often small worlds, which means that one can travel between nodes in this network by visiting only a small number of nodes compared to the network size. If we randomly select two users in Facebook, they are connected via only 4 other users on average. If you compare this number to the billion users the network actually has, this distance definitely deserves the term small.
Facebook is a small-world network
These small distances are partly responsible for the fact that information on networks with small exponents can spread very efficiently. This influences what the best strategy is to contain it. Something that can be very important if the information that is spreading is false. On the other hand, networks with small exponents are more resilient to attacks that remove connections. This happens for example when a hacker disrupts communication between servers on the internet.
In conclusion, if the degrees of a network follow a power-law, one can gain significant insight into the behavior of this network by simply estimating the exponent.
Are there many scale-free networks or very few?
Because of the significance of the power-law exponent, the early years of network science were filled with articles where researchers analyzed the degrees of real-world networks, trying to see if they were power-laws and estimating the exponent. To their surprise they found many cases where this exponent was estimated to be between 2 and 3. This led to the believe that most networks are scale-free and thus allowed them to make universal statements about the behavior of real-world networks.
However, over the last decade, these claims have led to discussions and at times heated debates. Researchers can’t agree on what is means for a degree distribution to be power-law. They have never been explicit about this and all have their own definition in mind. Often, they can only agree on the intuition behind the concept. That makes it almost impossible to have scientific discussions about the topic. This leads to the other problem: “How to properly estimate the power-law exponent of a degree distribution?” If researchers cannot agree on what a power-law is, how can they analyze them in networks. It is as if two carpenters are standing around a chair and arguing about whether or not it is a good chair, with one carpenter thinking of a chair as a beach chair while the other has a chesterfield armchair in mind.
At the end of 2018 a group of researchers published a paper in which they claimed that scale-free networks are actually rare. For their approach however, they relied on a very restrictive definition of what a power-law is. This created even more controversy in the debate on scale-free networks. Many researcher disagreed with this claim, arguing that no real networks would satisfy this definition. Others were happy to have some definition they could test, even though it could be too restrictive.
The 2018 paper defines a power-law degree distribution as a distribution for which (the fraction of nodes with degree ) behaves exactly like for all larger than some value . This definition allows for small degrees to be distributed in an arbitrary manner and only forces the large degree to be distributed according to an exact power-law. The problem with this definition is that many models for networks have degree distributions that do not satisfy this definition. One particular example is the Barabási-Albert model, which is often considered to be the architype model for scale-free networks. In this model decays as where is some function that converges to a constant as becomes large. By this new definition, the Barabási-Albert model, and many others would no longer create networks with power-law degrees. Which many researchers find unrealistic and undesirable.
Choosing between a rock and a hard place
The real problem is that this disagreement about what scale-free networks are and how to test if a network is scale-free can have far reaching consequences. Suppose, for example, that we want to use network analysis for designing effective strategies to combat the spreading of misinformation. Since the way information spreads in networks depends on the existence of large hubs, so does the choice of the right strategy. Thus it really matters if the network on which the misinformation spreads behaves like a scale-free network or not. If one group of researchers claims this is not the case, using this new restrictive definition, while another claims it is, based on a non-rigorous definition, then what should we do?
There are two obvious choices. However, each of them has the potential to undo years of research on networks. If we choose to stick with the restrictive definition we will likely conclude that scale-free networks are rare and as a consequence lose many results regarding the behavior of networks. This actually does not have to be true, since the behavior observed for scale-free networks could remain valid if we consider other, less restrictive, definitions. On the other hand, if we decide to continue with classifying scale-free networks using intuitions that lack a rigorous foundation we can end up making claims about the behavior of networks that are wrong.
To really resolve this problem, we need a proper definition of power-law degrees and scale-free networks. But how should we define these notions in such a way that it is maximally inclusive in capturing the associated intuitions and still allows us to estimate their presence among networks in the real world?
Extreme event mathematics
This is where mathematics enters the stage. More precisely the field of mathematics that studies extreme events. These are events that do not occur often but can have a large impact, such as earthquakes and tsunamis, or the resulting very large claim amounts with insurance companies.
We can think of seeing nodes with large degrees as such an extreme event; there are not that many of them but they can have a significant impact on the network.
A key tool in this field of extreme-value theory is the so-called Extreme Value Index (EVI) of a distribution. This index can be estimated from the data and tells you how large the extreme values can actually be. For example, the maximal strength of an earthquake or the largest claims an insurance company is expected to receive. In the context of Twitter, extreme events can correspond to observing a user with a very large number of followers.
Using extreme value theory we can properly define scalle-free networks
From the depths comes a solution
The connection between the Extreme Value Index and power-laws comes from a deep result in extreme-value theory. This result tells us that the distributions with positive index behave like power-laws, in a way that corresponds with the long standing intuition of network scientists. More precisely, distributions with positive index belong to the class of so-called regularly varying functions. This class includes the restrictive definition used to conclude that scale-free networks are rare, but contains many other functions which have similar mathematical properties.
A regularly varying function has the form . Here is a function that is said to vary slowly at infinity. Mathematically, this means that for any . Specific examples of slowly-varying functions are constant functions , logarithms and functions that converge to a constant as becomes large. The idea is that for large , the influence of this slowly varying function is negligible compared to the . In particular, if we make a log-log plot of these functions, it will look like a straight line with a negative slope. This is precisely the intuition behind the concept of power-law degrees that researchers have. Thus these functions are the perfect definition of power-laws.
Distributions with positive EVI are thus the best definition for capturing the intuition network scientists have concerning power-law degrees. In addition, the EVI is directly related to the power-law exponent, which was so crucial for the behavior of networks. Therefore, by estimating the EVI of degree distributions in networks we can solve both problems. We say the degrees behave like a power-law if the EVI is positive and call the network scale-free precisely when the corresponding estimated exponent is between 2 and 3.
Finally, since estimation techniques for the EVI have been in development since the 1950’s, a variety of powerful and precise estimation tools are readily available to use. This way, mathematics gives us a powerful notion of a scale-free network, using the right combination of a broad but precise definition, while at the same time providing researchers with tools to test this on real-world networks.
It is as if we can give those two carpenters a mathematical definition of a chair that captures both their ideas, as well as a machine that can tell them how good the chair in front of them is. The Extreme-Value approach to scale-free networks will aid networks scientist in engaging in productive scientific discussions on the topic. This will create a better understanding of scale-free networks and their behavior, while still being able to rely on known results. Thus saving decades of network research from the trash bin.
The visualizations of the scale-free networks were made by Yuntao Jia, Jared Hoberock, Michael Garlang and John Hart and published in "On the Visualization of Social and other Scale-Free Networks". The featured image was made by P.J. Lamberson and can be found here.[
Many networks, from technological to social networks, and from the world-wide web to collaboration networks, have a hub-like structure. Why is this the case, and why are they not much more homogeneous?
Have you ever wondered what makes a video go viral? Or how it is possible that they can spread so quickly? Maybe you didn't (that's fine), but many economists, marketeers, and even mathematicians have wondered.
How are elements in real-world networks connected? That is the question we aim to answer in this post. Most real-world networks turn out to be extremely inhomogeneous.
Have you ever wondered what mathematicians mean when they talk about mathematical models of real-life phenomena? And what can such a model tell us about the network-phenomenon we are studying?
An echo chamber is a community wherein the same opinions are bounced around, endlessly ‘echoing’ with barely any change. And as they do, any other opinion is shunned, pushed aside, and eventually just rejected without consideration.
