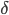Some webpages are enormously popular, and many thousands of other webpages link to them. Yet, most webpages have only few, or even no, other webpages that link to them.
Some people have millions of followers on Twitter, while most only have few. If a Twitter user with lots of followers retweets your post, then it is much more likely to go viral, so these highly- connected super-spreaders, sometimes also called hubs, play a very important role in spreading information. Many networks, from technological to social networks, and from the world-wide web to collaboration networks, have such a hub-like structure. Why is this the case, and why are they not much more homogeneous?
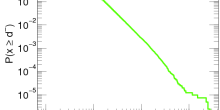
Jane is very excited. Yesterday, in her most popular class `Documentary Making' at the Film Academy, she was assigned to write an essay about collaboration between actors, with the aim to make a documentary about it. While most of her fellow students planned to describe qualitatively how famous actor duos such as Ryan Gosling and Emma Stone, or Julia Roberts and Brad Pitt, interact in their movies, she was intrigued about how such collaborations could be investigated quantitatively.
She remembered the Kevin Bacon game, a prank of a few computer science students from the University of Virginia, who challenged each other to find short connections between their favorite actors and Kevin Bacon, and built a website about this. Could she use this for her assignment? And would it be possible to use this to investigate how popular actors serve as role models for others, and inspire other actors while playing at the same movie set?
Jane looked up the website about the Oracle of Kevin Bacon, as the challenge is called, and realized that on that site, a tremendous amount of data could be downloaded about collaborations between actors through the Internet Movie Data base (IMDb). This data base describes collaborations between all actors as a network.
Two actors are connected in the network if they have played in the same movie.
A network is a collection of elements with connections between them. In the IMDb example, the elements are the actors and two actors are connected when they have both played in the same movie. This is just one example of a network and there are plenty of others.
In the Internet, the elements are routers that are connected to one another by physical cables. In the world-wide web, the elements are webpages that are connected by hyperlinks, and in social networks such as FaceBook, the elements are people connected to each other by friendships.
Many of these networks are very large in that they have several million elements. It is not even known how large the world-wide web is, but certainly it consist of more than a trillion webpages. That is a 1 followed by 12 zeroes.
Jane realized that the Internet Movie Data base offered her a wealth of quantitative information about collaboration patterns between actors, and she was eager to investigate those. She had not realized just how much information was really hidden there, and how networked this data really was!
Jane downloaded the IMDb data, and started doing an exploratory data analysis. Here, she was lucky to have taken a statistics course in her bachelor, so she knew how to juggle around big data sets. Because indeed the data set was big: it contains information about more than a million actors and over five million movies!
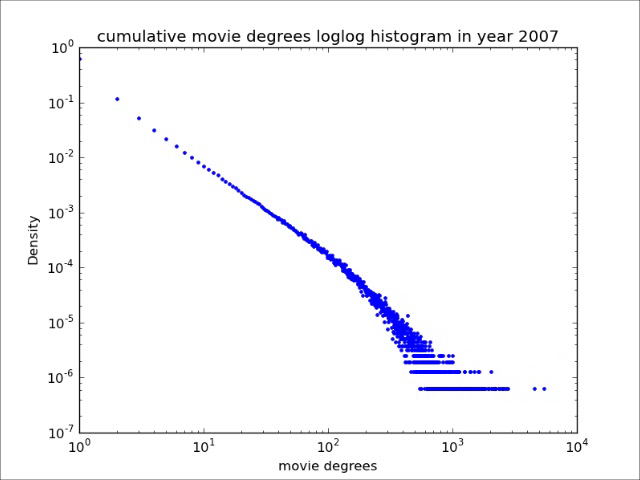
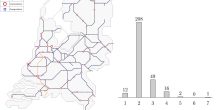
After hours of painstaking work to massage the data into a workable format, she was ready to analyse it. She started with the basics, namely, the data about how many neighbors actors in the IMDb have. She plotted this distribution.
On the horizontal axis in this plot we see the degree of an actor in the movie network. The degree of an actor is a number representing the number of other actors that this actor is connected to in the network. And being connected in the network means that they have played in the same movie. A blue point in this plot represents the fraction of actors in the network with that given degree. Take the first point on the left for example, it means that 10% of the actors in the network is connected to, or else have collaborated with, two other actors. Hence the points on the left represent actors who don't have many collaborations yet. On the other side of the figure, the points on the ``fat tail" on the right represent actors with many collaborations. The furthermost point for example shows that there is a very small fraction, almost 0.000001% of all the actors, that has collaborated with almost a thousand other actors.
Jane was rather surprised to see that while the average number of actors that an actor has worked with is not so large, there are actors with an enormous number of neighbors, up to several tens of thousands. She thought that the successful actors act as role models, and inspire other actors while playing at the same movie set. With the fact that there are actors who have worked together with so many fellow actors, such role models could play a highly profound role indeed, which would make her essay all the more exciting!
The number of elements that an element in a network is connected to is called its degree. Jane has found that there are many actors with lots of collaborators. In other words, there are many `hubs' in the collaboration network amongst actors, meaning network elements with enormously large degrees. This turns out to be a common feature of many real-world networks.
The IMDb network contains many hubs
And these hubs play an important role in the network, just like the actors with many connections can have an important role for actors within the film industry. Twitter users with many followers are the hubs in the Twitter network, and their posts receive much more attention than posts by users with hardly any followers. In turn, if a post is retweeted by one of the Twitter users with many followers, the post is much more likely to go viral. Webpages that have many links to them are visited much more often, and are thus good places for advertisements.
The histogram of the number of connections per element in a network is called the degree distribution, and it has received enormous attention in network science, as it is a signature feature of the network. Remarkably, even the degree distributions of many real-world networks are similar: the degree distribution of web pages in the world-wide web is similar to that of actors in the IMDb!
In this video we see that every year nodes of higher degree appear. This increase in the degrees of the nodes corresponds to actors becoming more popular.
While investigating the IMDb, Jane realized that the IMBb also contains time stamps of the releases of the movies it contains. Since these movies create the connections between actors, she decided to plot how the degree distribution changes between 1940 and 2007. Being a film academy student, she realized that she could even display it as a movie, plotting the degree distribution for different years as different frames. She was quite surprised by the result: this movie was rather smooth, and was getting smoother as the network became larger. Why is this? Are there organising principles in how actors start working together that give rise to such an effect?
Jane was quite puzzled by this movie. It was obvious to her that she was onto something, but there were many things that she did not understand. How did the hubs in the IMDb collaboration network arise? That hubs are important was now clear to her, but why and how they arise much less so! And why does the degree distribution evolve so smoothly? She decided to check whether there was a simple explanation for this phenomenon. Could it be that actors who already have a large degree are more likely to be involved in another movie, thus making their degree even larger? In other words, could it be the dynamics of the network formation that gives rise to such hubs?2
Instructions for the animation: The animation shows how the network is being generated. Each new point will connect to the points that were already present; the point to which a new point will be connected is chosen according to the degree of the existing points. If a point has a higher degree, then a new point will connect to that point with higher probability. This resembles the actor network. A new actor is more probable to cooperate, or connect, to an actor who has collaborated with many other actors, and hence has a high degree in the network. The parameter indicates how strong this rich-get-rich phenomenon is, smaller means that it is more likely that new points connect to older points with higher degrees.
Network science comes into play
Network science studies networks from a scientific perspective, by studying their empirical properties, as well as by proposing models for networks that have a similar structure as the real-world networks of interest. Most network models have a fixed number of elements and describe how connections between the elements arise: the networks are static. However, as Jane observed for the IMDb, most networks grow in time and are thus dynamic. This sparks the question precisely how networks grow.
In the IMDb example, probably the actors with many connections, that form the hubs of the network, are the popular actors, and these are more likely to play in the next blockbuster, so that their degrees will grow even larger:
the rich get richer!
Here we think of actors that have a large degree in the network as being `rich', and for them it is more likely to be playing in yet another movie than for the average actor, so that their degrees will go up even more.
In a class of models for such dynamic networks, called preferential attachment models, the network evolves by adding the network elements one by one, and connecting them to older network elements with probabilities that are proportional to their current degrees. In the IMDb context, this would mean that a young actor is more likely to play together with an older actor that is already famous and thus has large degree in the network. Much is known about preferential attachment models. In general, they have a hub-like structure where the number of neighbors of hubs is several orders of magnitude larger than the average.
Popular actors are more likely to play in another movie, thus making their degree even larger!
Even though the mechanism is very simple, it offers a possible explanation for the abundance of hub-structured networks: it is all due to the dynamics! Below you can see an animation that shows how such a network grows.
Further, in preferential attachment models, the degree distribution stabilizes, in that the proportions of elements with a given number of connections converges when the network grows, very alike what Jane observed in the IMDb network of actors. Below is a demo that shows how such networks look like, and shows the degree distribution that corresponds to them.
Reading about these theoretical findings, a click formed in Jane's head. She immediately knew what the conclusion of her essay would be: Actors who have co-acted with many others are more likely to co-act with even more of them. In other words, collaborations between actors follow a rich-get-richer pattern. This simple pattern explains why the movie of the evolution of the number of neighbors in the network looks so smooth. She was sure that this essay would give her fellow students much to think about, and she was looking forward to their reactions!
Have you ever wondered what makes a video go viral? Or how it is possible that they can spread so quickly? Maybe you didn't (that's fine), but many economists, marketeers, and even mathematicians have wondered.
A graph consists of objects called vertices and connections between them called edges. For every vertex, we can count how many neighbors it has, which is called its degree.
How are elements in real-world networks connected? That is the question we aim to answer in this post. Most real-world networks turn out to be extremely inhomogeneous.
