On the 6th of April David Aldous received the Brouwer Medal 2020 for his contributions to probability theory. The prize was supposed to be awarded last year but due to the cancelation of the Dutch Mathematics Conference (NMC) the ceremony was postponed. The prize was awarded this year during the Scientific Days of the NMC2021, which were held online due to the COVID-restrictions.
The Brouwer Medal is a triennial award presented by the Royal Dutch Mathematical Society and the Royal Netherlands Academy of Sciences. The award carries the name of the Dutch mathematician Luitzen Egbertus Jan Brouwer (1881 – 1966), who was a professor at the University of Amsterdam. The Brouwer Medal is The Netherlands’ most prestigious award in mathematics.
David Aldous is an emeritus professor in the statistics department in the University of California at Berkley. Anyone working in or with a scientific interest in probability theory or statistics will definitely encounter or have encountered his name at some point. The scientific committee decided to award the Brouwer medal to Aldous for his significant contributions in both theoretical and applied probability.
Photo from the website of the NMC 2021
Let me cite the words of Frank den Hollander, member of the nomination committee
The work of David covers both pure and applied probability, and is characterised by great originality, combined with depth, breadth and beauty. David has introduced a wealth of new concepts, which have had an enormous impact not only on probability itself, but also on other scientific fields. David has initiated flourishing new areas of research and has inspired researchers worldwide.
In particular, the following scientific contributions of David Aldous were highlighted during the award ceremony:
The ALOHA protocol, which is used in communication networks and was modified after Aldous proved that the original protocol was flawed.
The probabilistic analysis of performance of algorithms in combinatorial optimization.
The Aldous tightness criterion, which provides a connection between stopping times and tightness and links general theory of stochastic processes and weak convergence.
The cut-off phenomenon for mixing times, a new concept for Markov processes pioneered with Persi Diaconis.
His landmark series of papers on limits of tree-like structures which lead to a better understanding of universality.
His work on exchangeability that led to extensions of de Finetti’s theorem and became a major tool in different areas of probability theory, including random graph theory.
Local weak convergence, a key concept for convergence in random graphs.
The Poisson clumping heuristic, a guiding notion for description of rare events with a wide range of applications
His description of critical clusters in the Erdős–Rényi model for random graphs.
Miscellaneous work on scale-invariant random spatial networks, discrete spatial networks, flows through random networks, recursive distributional equations, and stochastic models for phylogenetic trees.
Some, or maybe even all, of these concepts may say nothing to you but that is fine. I am myself familiar with some of them, not all of them, but believe me if I say that they are all beautiful mathematical concepts and theories to dive in and to learn about. Each one of them corresponds to a beautiful small, nevertheless very important, piece of modern probability theory. All ten of them are elegant and very challenging to work on, demanding curiosity, creativity, hard work and persistence.
David Aldous also maintains an incredibly rich website, named “Probability and the real world” which aims at popularizing probability theory. On his website you can find opinion articles on various topics, from aspects of the real world that involve chance to teaching of probability theory, and opinion blogs on the use of mathematical models. One particular discussion that I found very intriguing concerned how we interpret everyday information to make estimations. I found this very interesting because it questioned the way I learned to think of probabilities and estimations. Below I present my version of what I read on Aldous’s website, most of it is taken from the original blog, but I elaborate a little bit more on two crucial steps.
The twins example
Reading various blogs on Aldous's website I started questioning multiple school-book examples used to teach probability theory. To cite Aldous’s words:
“I assert one can find many examples where the formal math setup can lead you astray.”
Isn’t this intriguing? How can the formal math setup lead anyone astray? Well, everyday experiments are much more versatile than school-book simplifications. The twins example concerns the following hypothetical everyday life scenario:
“In casual conversation with a stranger in the next airplane seat, you ask "do you have children?" and the response is "yes, two boys". Based on this, what is the chance that the two boys are twins?”
The first step to consider is the following: is the answer to this question purely given by the percentage of families with only two boys that are also twins? This likelihood is given by
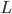= (number of families with only two twin boys) / (number of families with only two boys).
Here we only need to consider families with two boys (twins or not) since from the answer given we already know this information. This percentage turns out to be approximately 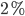, see the blog post for a more detailed discussion. Is also the chance in the twin problem equal to 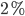? Aldous says that he would bet his money on a significantly smaller chance. Why is this?
Because when a parent answers a question like “do you have children?” probably the answer will convey some additional information about the children. Parents having children that are twins may often mention it when asked about them for example. Hence if their answer does not convey any information on the children being twins maybe they are more likely to be parents of non-twins. How can we use this extra intuition to make a more accurate estimate of the desired chance? Aldous defines two probabilities,
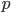= Probability that a parent of two twins answers in a way that it is not possible to infer if the siblings are twins
and
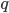= Probability that a parent of two non-twins answers in a way that it is not possible to infer if the siblings are non-twins.
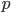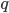If I had to make a guess on the value of and I would say that 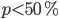(parents of twins relatively often mention it) while 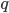seems to be close to 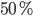(I leave it to yourself to think why 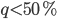and 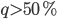don’t seem very realistic, initially I wrote it down but then I thought it is too nice to spoil it). The case 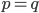, which would lead to 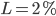being a good estimate of the chance we are looking for (why?), also doesn't seem very realistic, since parents like to talk about what makes their loved ones so special. Aldous gives an guess - estimate for 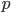equal to 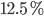and for 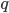equal to 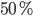. Having these estimates how can we compute the desired chance?
The answer of the parent “yes, two boys” doesn’t allow us to infer if the boys are twins or not, hence, since 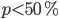, it seems more likely that the parent we asked is not a parent of twins. We see that the nature of the given answer implies that a good estimate of the desired chance might be 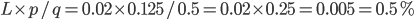much lower than the likelihood .
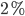Aldous’s writes on his website:
“an approximate answer to the right problem is worth a good deal more than an exact answer to an approximate problem.”
This is an idea that I find very interesting to think about, along with the riddle above of course, that shows that everyday experiences demand some flexibility in order to grab their essence.
In times of war, secure communication can be the difference between life and death, or even winning or losing a war. The first to patent a rotor machine in Europe was Arthur Scherbius in 1918. Scherbius’ version of the rotor machine became a commercial success, unlike the other patented machines. Scherbius named his machine Enigma.
On a quiet afternoon, professor Meth is working in her office in Leiden on some tantalizing mathematics problems. Suddenly, someone knocking on her door nervously disrupts the silence.
The new date for this event is April the 7th 2022 from 19:00 to 21:00 uur. In April the Dutch Academy of Sciences and Arts (KMAW) organizes the "Evening of the Abel prize", a yearly event with as goal to discuss aspects of the research of the latest Abel prize laureates. The event is meant for a […]
The Turing Award of 2020 was awarded to Alfred Vaino Aho, from Columbia University, and Jeffrey David Ullman, from Stanford University, whose work has contributed greatly to the way computers are controlled.
= (number of families with only two twin boys) / (number of families with only two boys).
, see the blog post for a more detailed discussion. Is also the chance in the twin problem equal to 
= Probability that a parent of two twins answers in a way that it is not possible to infer if the siblings are twins
= Probability that a parent of two non-twins answers in a way that it is not possible to infer if the siblings are non-twins.
(parents of twins relatively often mention it) while 
(I leave it to yourself to think why 
and 
don’t seem very realistic, initially I wrote it down but then I thought it is too nice to spoil it). The case 
, which would lead to 
being a good estimate of the chance we are looking for (why?), also doesn't seem very realistic, since parents like to talk about what makes their loved ones so special. Aldous gives an guess - estimate for 
and for 
much lower than the likelihood 
