Most people are familiar with the game Set. A bunch of cards are laid out, and players race to spot a triple where each feature is either all the same or all different. Such a triple is called a “set.” It’s a game of sharp eyes and quick thinking.
In the original game, there are four features (color, shape, number, and shading) with three options each. For my school research project, I added a fourth option to each feature: an extra color, shape, number, and shading. In the new version, a set consists of four cards instead of three. This version of the game didn’t exist yet, so I had it made. In my project, I explored the mathematical principles behind both versions of the game. The main research question I investigated was:
What are the mathematical consequences of increasing the number of options for each feature in the game Set?
The first and most practical consequence was playability. While the original game is fun and playable, the version with four options turns out to be nearly impossible to play and not much fun. For starters, it takes way too long: the deck is more than three times as large. Furthermore, finding a valid set of four cards isn’t easy. In the regular Set game, any two cards point to exactly one third card that completes the set. But in the extended version, two cards can match with several possible third cards (though most cards are not a match). Then you still need a fourth card, which usually isn’t even on the table. All these factors make the game practically unplayable.
Luckily, I didn’t make the game just to play it, I made it to research it! My project centered around three main questions:
- How can both versions of the game be represented mathematically?
- What’s the maximum number of cards you can lay out without forming a set?
- What’s the total number of sets in each version of the game?
I explored the answers to all three questions for both versions of the game. Then I compared the results from the original Set game with those from my expanded version. In this article, I’ll focus only on the third question: the total number of sets.
Calculating the total number of sets in the game with three options is fairly straightforward. You can use the fact that for any two arbitrary cards, there’s exactly one third card that completes the set. There are  cards in the game, so the number of possible sets is
cards in the game, so the number of possible sets is  .
.
However, this count includes a lot of duplicates! Combinations like 123, 132, 213, 231, 321, and 312 are all counted separately, even though they form the same set. Since each set consists of three cards, every unique set is counted  times. To find the actual number of distinct sets, we divide the total by the number of duplicate permutations. So the total number of sets is
times. To find the actual number of distinct sets, we divide the total by the number of duplicate permutations. So the total number of sets is  .
.

The extended version of the Set game made by Femke.
Unfortunately, this “simple” method of calculation breaks down when there are four options. That’s because the number of possible third cards depends on how different the first two cards are. If the first two cards differ in only one feature, then there’s only one possible set to form. But if the first two cards differ in all features, then (in the version with four options) there are still eight different sets that can be formed.
Since each type of set requires a different calculation, we need to distinguish between four groups: sets where all features are different, sets where one feature is the same, sets where two features are the same, sets where three features are the same
Each group requires its own separate calculation, and the results must be added together. Below is the breakdown for each group.
Sets where all features are different: For the first card, you can choose any of the 256 cards in the deck. For the second card, you must pick one that differs completely from the first. There are 81 such cards (you’re missing one option for each feature, so you’re left with a base game of three options per feature). The third card must be completely different from both previous cards. There are 16 possibilities for that (a game with two options per feature). For the fourth and final card, only one possibility remains. The calculation becomes: \begin{equation} 256 * 81 * 16 * 1 = 331,776 \text{ sets.} \end{equation}
Sets where one feature is the same: For the first card, you can still choose from 256 cards, and for the second card, one feature must remain the same. Suppose you picked the first card in the top left corner (a single purple dotted oval) and you want to keep the color feature the same. The cards are laid out in batches of sixteen, in four rows and four columns. To keep the color the same, you must choose cards from the first row. But all the cards in the first batch of sixteen have the same shape. The other three batches of sixteen do contain cards, each with nine cards:
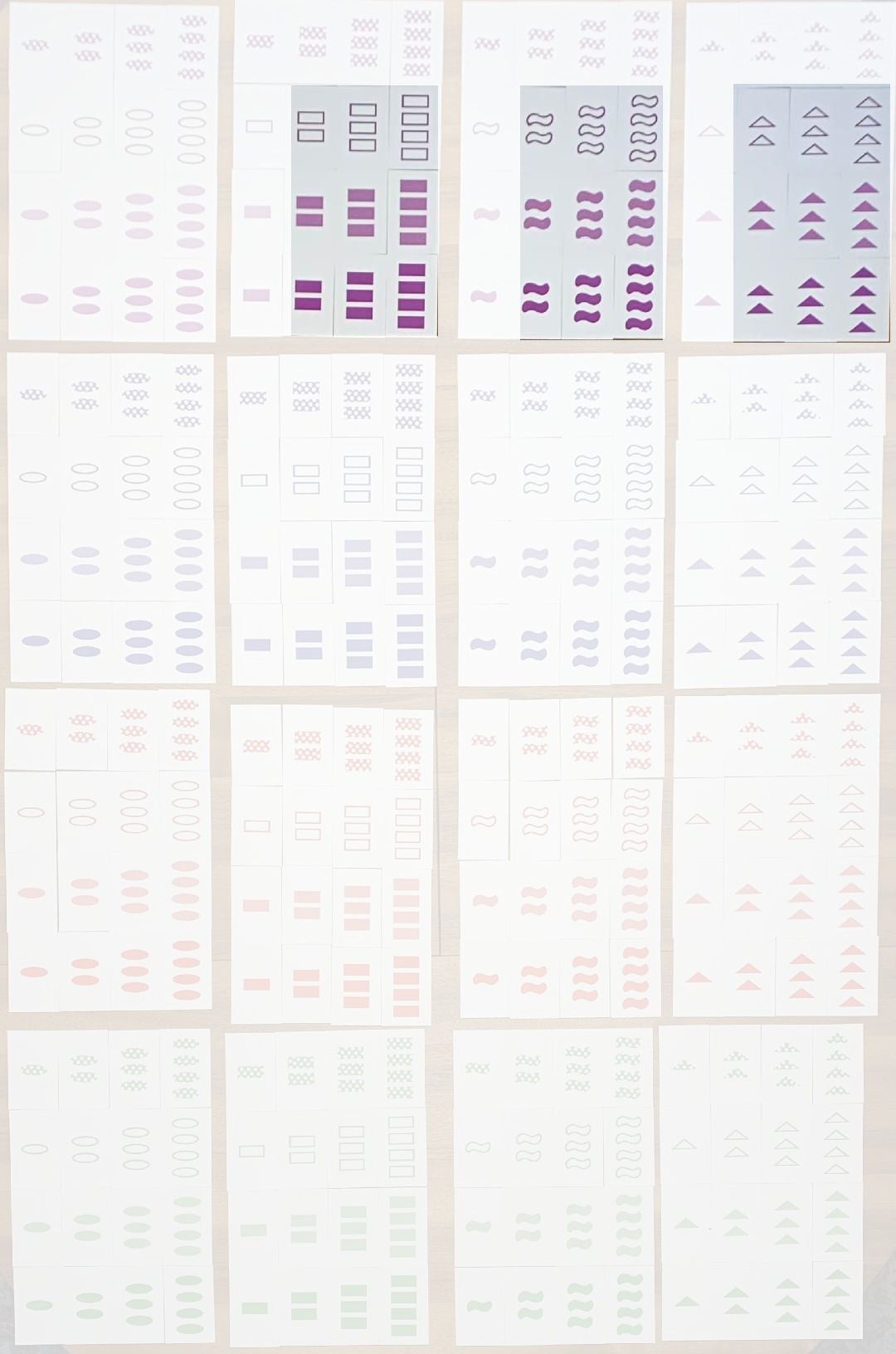
So that gives  possible cards. The third card must also be purple. The other three features must be different from those of the first two cards. For each of these three features, you now have two options. So for the third card, there are
possible cards. The third card must also be purple. The other three features must be different from those of the first two cards. For each of these three features, you now have two options. So for the third card, there are  options. For the final card, only one possibility remains.
options. For the final card, only one possibility remains.
In the example, we chose to build a set where the color stayed the same. But we could have chosen a different feature instead. Therefore, we also need to multiply by 4 to get the total number of sets. The total number of sets becomes:
\begin{equation}
4 * 256 * 27 * 8 * 1 = 221,184 \text{ sets.}
\end{equation}
Now I challenge you to verify for yourself that the number of sets where two features are the same totals 55,296 sets and the number of sets where three features are the same totals 6,144 sets.
To calculate the total number of possible sets in the collection, the four different counts must be added together. The calculation looks like this: \begin{equation} 331,776 + 221,184 + 55,296 + 6,144 = 614,400 \text{ sets.} \end{equation}
But even here, there are duplicate counts. Since a set consists of four cards, each set has been counted exactly  times. So the total of 614,400 must be divided by that number. The total number of distinct sets is: \begin{equation} 614,400 / 4! = 25,600 \text{ sets.} \end{equation}
times. So the total of 614,400 must be divided by that number. The total number of distinct sets is: \begin{equation} 614,400 / 4! = 25,600 \text{ sets.} \end{equation}
Okay, now we know how many sets exist in the game with four options, but what about more than four options? Let’s try to create a general formula that allows you to calculate the number of sets for any number of options.
For this calculation, we again divide the sets into four groups, just like in the calculation for four options. We call the number of options 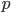 and the total number of sets
and the total number of sets 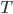 . A set then consists of
. A set then consists of 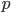 cards, just as a set with three options consisted of three cards, and a set with four options consisted of four cards.
cards, just as a set with three options consisted of three cards, and a set with four options consisted of four cards.
Sets where all features are different: For the first card, there are  possibilities (the total number of cards). Since the second card must be completely different, one option is eliminated for each feature. If you remove all these cards, you’re left with the same game but with one fewer option. So for the second card, there are
possibilities (the total number of cards). Since the second card must be completely different, one option is eliminated for each feature. If you remove all these cards, you’re left with the same game but with one fewer option. So for the second card, there are  possibilities remaining. Applying the same reasoning to the third card, you’ll find there are
possibilities remaining. Applying the same reasoning to the third card, you’ll find there are  possibilities. This pattern continues all the way to the last card. A set consists of
possibilities. This pattern continues all the way to the last card. A set consists of 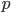 cards, so you get a product of
cards, so you get a product of 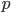 terms. The final term is
terms. The final term is  . This is written as follows: \begin{equation} p^4 * (p-1)^4 * (p-2)^4 \cdots 1^4. \end{equation}
. This is written as follows: \begin{equation} p^4 * (p-1)^4 * (p-2)^4 \cdots 1^4. \end{equation}
Since all these terms are raised to the fourth power, you can factor out the exponent, as shown below:
\begin{equation} \left( p * (p-1) * (p-2) * \cdots * 1\right)^4. \end{equation}
This may seem like a small change, but the expression inside the parentheses is the same as  . That simplifies the calculation to
. That simplifies the calculation to  .
.
Sets where one feature is the same: For the first card, there are again  possibilities. There are also four possible features that we can choose to keep the same. For the second card, three features must be different from the first card. For each of those three features, there are
possibilities. There are also four possible features that we can choose to keep the same. For the second card, three features must be different from the first card. For each of those three features, there are  options. So for the second card, there are
options. So for the second card, there are  options. For the third card, each feature has
options. For the third card, each feature has  remaining options, resulting in
remaining options, resulting in  possibilities. This pattern continues until the final card. The total number of sets in this group is therefore:
possibilities. This pattern continues until the final card. The total number of sets in this group is therefore:
\begin{equation}
4 \cdot p^4 \cdot (p-1)^3 \cdot (p-2)^3 \cdots 2^3.
\end{equation}
This can be rewritten as:
\begin{equation}
4p \cdot \left(p \cdot (p-1) \cdot (p-2) \cdots 2 \right)^3 = 4p \cdot p!^3.
\end{equation}
Now that we’ve looked at how to perform the calculation, it’s up to you to work out the calculations for sets where two and three features are the same.
If you’ve done the calculations correctly, you’ll find that the total number of sets is as follows:
\begin{equation}
1p^0 * p!^4 + 4p^1 * p!^3 + 6p^2 * p!^2 + 4p^3 * p!^1.
\end{equation}
You may be familiar with Pascal’s triangle. It’s a triangle of numbers that reveals many mathematical patterns.
The first five levels of Pascal's triangle, found on mathisfun.com
You can also use this triangle to quickly expand expressions with higher powers. For example, if you want to expand a fourth power, you get the following: \begin{equation} (a+b)^4 = 1a^4b^0 + 4a^3b^1 + 6a^2b^2 + 4a^1b^3 + 1a^0b^4 \end{equation}
This expansion looks quite similar to the formula we’ve created. That would mean:  and
and  . This is almost entirely correct, except that one term is missing:
. This is almost entirely correct, except that one term is missing:  , because there is no
, because there is no  . So if we want to rewrite the formula using parentheses, we would need to remove that term. Also, we’ve counted some sets multiple times in this formula, which means we still need to divide the total by
. So if we want to rewrite the formula using parentheses, we would need to remove that term. Also, we’ve counted some sets multiple times in this formula, which means we still need to divide the total by  . The final formula then becomes:
. The final formula then becomes:
\begin{equation} T = \frac{(p+p!)^4 - p^4}{p!}. \end{equation}
To conclude, I examined what happens when the well-known game Set is expanded from three to four options per feature. While the original game ia playable and easy to follow, the expanded version turns out to be much more complex, both in terms of practical playability and mathematical structure.
This article was translated by the Network Pages from Dutch to English, with the help of Microsoft Copilot. The original Dutch article can be found here.