
On Wednesday the 17th of March the Abel prize was awarded to mathematicians László Lovász and Avi Wigderson
"for their foundational contributions to theoretical computer science and discrete mathematics, and their leading role in shaping them into central fields of modern mathematics."
Theoretical computer science (TCS) is a discipline that focuses on the power and the limitations of computing. The two primary scopes of TCS are designing algorithms to solve problems; and investigating computational complexity, which sheds light onto the computational efficiency of algorithms and the inherent complexity of computational problems. (Photo on the right: Avi Wigderson. Taken from the Abel Prize Photo Album. Copyright Andrea Kane - Institute for Advanced Study, Princeton, NJ USA).


Discrete mathematics (DM) is a field in mathematics that studies, as the name suggests, discrete objects, like graphs for example. Discrete mathematics and theoretical computer science have been two disciplines that have received tremendous attention in the last 120 years and have evolved almost as two siblings, helping each other in solving each one's problems. In this article, I want to discuss shortly a concept in modern mathematics pioneered by László Lovász, that of graph-limits. (Photo on the left: László Lovász. Taken from the Abel Prize Photo Album. Copyright Hungarian Academy of Sciences).
I chose to restrict my article to one (of the many) mathematical breakthroughs of L. Lovász, that of graph-limits, instead of giving a general overview of their accomplishments. This choice is due to two main reasons. First of all, I am quite familiar with graph-limits from my research, on the contrary, I am not very familiar with their research as a whole. Secondly, on the website of the Abel prize, you can find wonderful articles about L. Lovász and A. Wigderson, with a short biography and an overview of their work. Trying to give my overview of their work would be at best rephrasing what is written in these articles. The famous Lovász-Lenstra-Lenstra lattice reduction algorithm, some major contributions in graph theory, and A. Wigderson's work on Zero-knowledge proofs are also discussed in a very elegant matter. The work of L. Lovász on graph-limits is mentioned but not discussed in detail in these press-releases. There is thus no better time to say something about the very elegant mathematical theory of graph-limits.
Graph-limits
Many interesting structures and phenomena of the world can be described by networks. In many cases, such networks are very large, large in the sense that they have a large number of nodes and connections. As L. Lovász writes in the introduction of his book on this topic, "developing a mathematical theory of very large networks is an important challenge". This limit theory of graphs, which relies on a mathematical construction called graph-limits and which has emerged over the last two decades, is an approach to this challenge.
The theory of graph-limits was conceived by Lovász and his colleagues around 2000 when he was working at Microsoft Research. In the preface of his book, we can read how the first ideas on this mathematical theory were conceived.
"Within a couple of months in 2003, in the Theory Group of Microsoft Research in Redmond, Washington, three questions were asked by three colleagues. Michael Freedman, who was working on some very interesting ideas to design a quantum computer based on methods of algebraic topology, wanted to know which graph parameters (functions on finite graphs) can be represented as partition functions of models from statistical physics. Jennifer Chayes, who was studying internet models, asked whether there was a notion of “limit distribution” for sequences of graphs (rather than for sequences of numbers). Vera T. Sós, a visitor from Budapest interested in the phenomenon of quasirandomness and its connections to the Regularity Lemma, suggested to generalize results about quasirandom graphs to multitype quasirandom graphs. It turned out that these questions were very closely related, and the ideas which we developed for the answers have motivated much of my research for the next years."
A beautiful and very strong contribution of this theory is that it lays a bridge between the mathematical field of graph theory and analysis. Analysis is a field of mathematics known to all of us from high-school mathematics, it studies functions and limits. I am sure you remember these concepts, which at school probably didn't seem so appealing. The theory of graph-limits lays in a very natural and elegant way a bridge between these two seemingly distinct fields of mathematics. It dictates that you can represent a graph as a function, which allows you to use all the machinery scientists have developed for the analysis of functions, to study graphs. And the most astonishing about this theory, or maybe better of this correspondence, is that it is very suitable for very large graphs. With graph theory you can study small graphs while large graphs are rather untraceable using conventional techniques, using the theory of graph-limits, or graphons, the study of very large graphs becomes possible. At the moment this theory is still being enriched and further developed by many researchers all over the world.
"Lovász is one of the founders of the theory of graphons. This theory plays a key role in analyzing limits of dense graphs, i.e. graphs where a positive fraction of all possible lines between the nodes are actually present. The theory of graphons links the combinatorics of graphs on the one hand and the functional analysis of graphons on the other, making it a powerful mathematical weapon in the study of dense complex networks." - Prof. Frank den Hollander
Let's have a look at how this works. Consider a graph 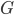 consisting of
consisting of  vertices and edges between some of the vertices. We can relate a simple function, denote it by
vertices and edges between some of the vertices. We can relate a simple function, denote it by 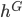 , to this graph which will take the value 1 when there will an edge between two vertices and equal to zero when there will be no edge between two vertices.
, to this graph which will take the value 1 when there will an edge between two vertices and equal to zero when there will be no edge between two vertices.
The function hence will look like this: for two vertices 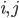
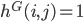 if there is an edge in
if there is an edge in 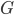 between the vertices
between the vertices  and
and 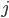 . If there is no edge between
. If there is no edge between  and
and 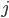 then
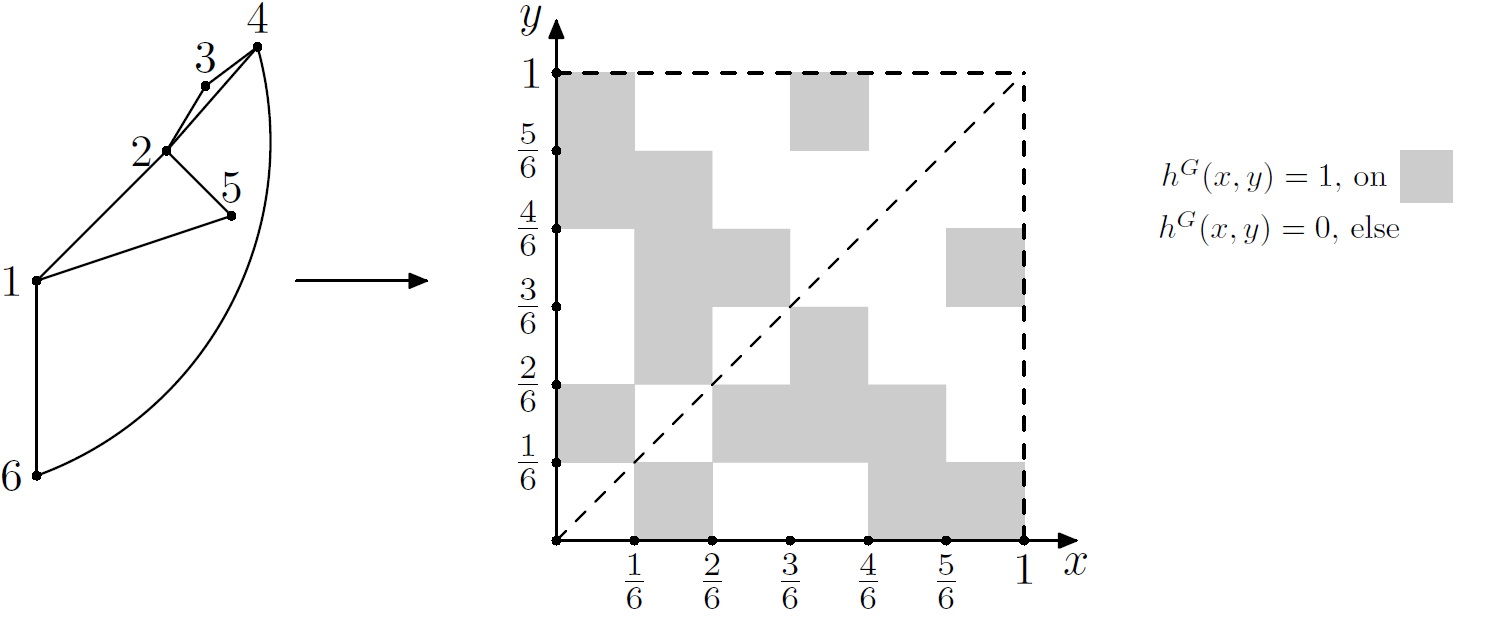
then 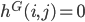 . Consider for example the graph in the picture on the right. This graph consists of 6 vertices and 8 edges. For this graph we have
. Consider for example the graph in the picture on the right. This graph consists of 6 vertices and 8 edges. For this graph we have 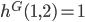 and
and 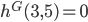 since there is no edge connecting vertices 3 and 5.
since there is no edge connecting vertices 3 and 5.
But this is not the crux of the theory of graph-limits. To understand the step connecting graph theory and analysis we need to push this function 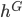 one step further. This function as defined above is a function whose argument is a pair
one step further. This function as defined above is a function whose argument is a pair 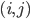 of vertices. The crux in the theory of graph-limits is to extend this function to a function
of vertices. The crux in the theory of graph-limits is to extend this function to a function 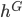 whose input is a pair of continuous variables
whose input is a pair of continuous variables 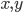 each one taking values between 0 and 1. The functions we learned at school were also functions whose argument was a continuous variable. Let's see how such a function will look like, suppose again that
each one taking values between 0 and 1. The functions we learned at school were also functions whose argument was a continuous variable. Let's see how such a function will look like, suppose again that 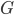 is a graph with
is a graph with  vertices. We divide the interval
vertices. We divide the interval ![[0,1]](https://www.networkpages.nl/wp-content/plugins/latex/cache/tex_ccfcd347d0bf65dc77afe01a3306a96b.gif) into
into  pieces, those are
pieces, those are ![[0, \frac{1}{n}], [\frac{1}{n}, \frac{2}{n}],...[\frac{n-1}{n}, 1]](https://www.networkpages.nl/wp-content/plugins/latex/cache/tex_bb8fc818bed9494de60169a3b5c42668.gif) . If there is an edge between vertices
. If there is an edge between vertices  and
and 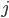 then we put
then we put 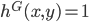 for all
for all 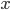 in the smaller interval
in the smaller interval ![[\frac{i-1}{n}, \frac{i}{n}]](https://www.networkpages.nl/wp-content/plugins/latex/cache/tex_32360e438e52b63b9c98d16582ac6149.gif) and for all
and for all 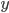 in the smaller interval
in the smaller interval ![[\frac{j-1}{n}, \frac{j}{n}]](https://www.networkpages.nl/wp-content/plugins/latex/cache/tex_8b70d83c39fcb3e48da3495f426a4e72.gif) . This function
. This function 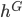 will be the graphon corresponding to the graph
will be the graphon corresponding to the graph 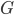 . The amazing observation is that you can do this for arbitrarily large graph sizes just by splitting the interval
. The amazing observation is that you can do this for arbitrarily large graph sizes just by splitting the interval ![[0,1]](https://www.networkpages.nl/wp-content/plugins/latex/cache/tex_ccfcd347d0bf65dc77afe01a3306a96b.gif) into smaller and smaller pieces. The following picture illustrates the graphon corresponding to the graph above.
into smaller and smaller pieces. The following picture illustrates the graphon corresponding to the graph above.
 The final touch is a rather technical one, which I don't want to discuss in detail but I think it is worth mentioning, the function
The final touch is a rather technical one, which I don't want to discuss in detail but I think it is worth mentioning, the function  is not entirely ready yet to be used, we need to apply a method from analysis so that it becomes invariant under permutations of the vertices! The idea I want to convey is that this modern theory allows machinery from analysis to be used to analyze large complex networks. The theory of graph-limits, or graphons, was firstly presented in two beautiful articles that I first read in the second year of my PhD. I still have a copy of them in my drawer in my office in Amsterdam. Lovász's work on graph-limits has received a lot of attention and has inspired a whole stream of research. To conclude, I remember reading recently, when I wrote a blog post on Ramsey numbers, that Ashwin Sah, a young mathematician who just finished his bachelor studies at MIT, used graph-limits to prove an important result concerning Ramsey numbers. Thanks to the work of these great mathematicians a lot of beautiful mathematical theories and results have been made possible.
is not entirely ready yet to be used, we need to apply a method from analysis so that it becomes invariant under permutations of the vertices! The idea I want to convey is that this modern theory allows machinery from analysis to be used to analyze large complex networks. The theory of graph-limits, or graphons, was firstly presented in two beautiful articles that I first read in the second year of my PhD. I still have a copy of them in my drawer in my office in Amsterdam. Lovász's work on graph-limits has received a lot of attention and has inspired a whole stream of research. To conclude, I remember reading recently, when I wrote a blog post on Ramsey numbers, that Ashwin Sah, a young mathematician who just finished his bachelor studies at MIT, used graph-limits to prove an important result concerning Ramsey numbers. Thanks to the work of these great mathematicians a lot of beautiful mathematical theories and results have been made possible.




