Synchronization is a phenomenon which has received a lot of attention in the last few decades. It is the mechanism by which a group of individuals that go through some periodic motion begin moving through the same parts of their cycles at the same time.
The way to model this is to have the individuals in the population interact with one another in such a way that the synchronization occurs. The art is then to come up with an interaction that most closely resembles the way in which synchronization occurs in nature. Probably the earliest writing on inanimate synchronization is due to the Dutch scientist Christiaan Huygens (1629-1695), who discovered that two pendulum clocks hanging from a common support (a wooden bar supported by two chairs, see Figure 1), kept in pace relative to each other such that the two pendulums always swung together (in opposite motion) and never varied. By Huygens this was called “sympathy of two clocks”. After some systematic experiments he found the source of the “sympathy”: the imperceptible motion of the bar to which the pendulum clocks were attached. Nowadays, the phenomenon described by Huygens (pendulums approaching and receding in opposite motions) is called anti-phase synchronization for obvious reasons.
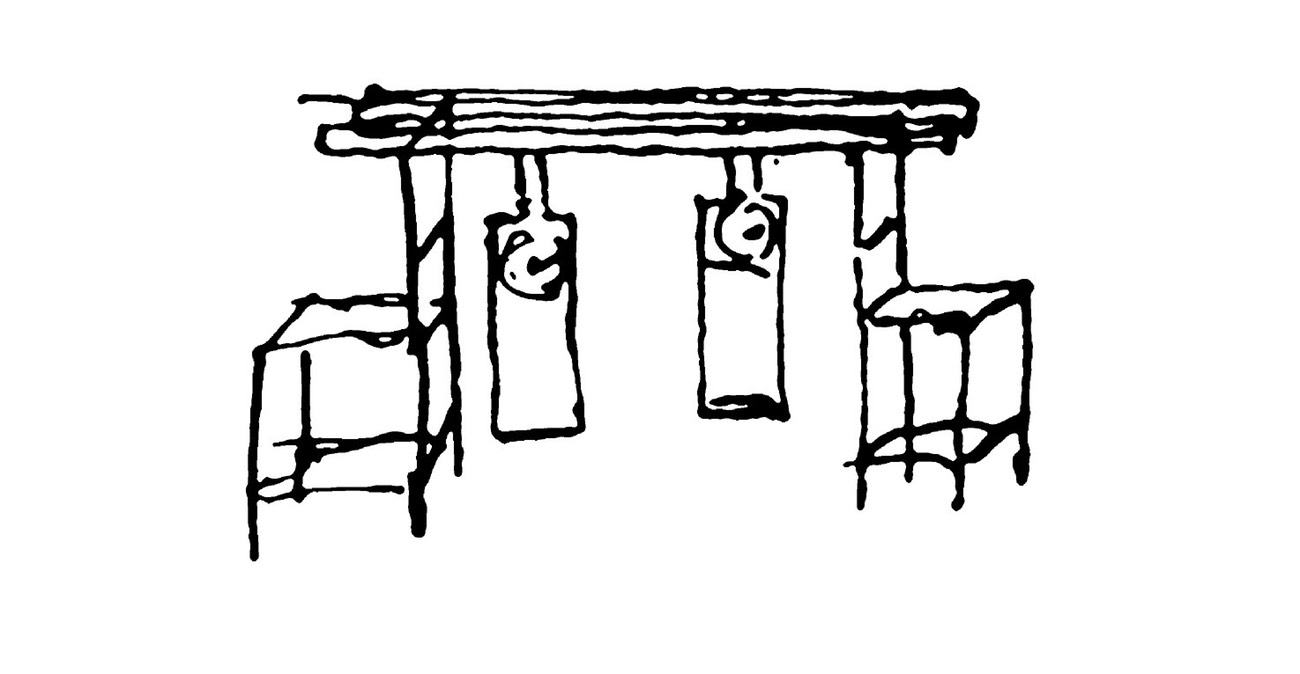
Figure 1: Sympathy of two clocks, drawing made by Huygens.
One of the simplest models conceived to date is called the Kuramoto model which models the interaction using the sine function. In the simplest case all individuals interact with all other individuals in the population. A more sophisticated model would use a network to describe which pairs of individuals interact. The occurrence of synchronization phenomena is overwhelming. To name a few examples:
Fireflies in south-east Asia or the Smoky mountains National park synchronize their flashing frequencies, which results in trees lightning up like Christmas trees.
Metronomes placed on a moving surface. No matter how you start the metronomes they will synchronize after some time
Applause: When people start clapping their hands they tend to adjust their pace of clapping to the clapping of nearby people.
Oscillations in the brain lead to certain electrical waves, such for example the -waves. Some diseases like epilepsy are thought to be related to ``over-synchronization'' of the brain. Hence synchronization is not always beneficial.
The so-called millennium bridge had to be closed shortly after being officially opened due to unexpected large sideways oscillations which were in fact due to people synchronizing their steps as a response the wobbling generated by the other people on the bridge; see also the link where Steven Strogatz nicely explains the phenomenon.
In a series of articles we will discuss how mathematicians and physicists study this wonderful phenomenon. One article concerns the standard Kuramoto model. In a follow up article we discuss the quantum version of the Kuramoto model and see a relation between quantum entaglement and synchronization. In a third article we discuss the future of the Internet, the quantum Internet, where synchronization plays an important role!
Conclusion
The body-clock is a complex network of neurons that is difficult to model mathematically, due to its many intricacies. Above we have seen that we can gain some understanding by using mathematics and simulations, but also that experiments uncovering an interesting phenomenon can play an important role in guiding mathematicians in making choices about which questions are interesting and worthwhile to study.
Specifically, we have found a possible mechanism for the different types of transitions to the phase-split state observed in experiments. Which transition occurs will depend on the interactions strengths, which may be different in different individuals. Much remains to be done in studying the two-community Kuramoto model, and even more when it comes to understanding the body-clock.
We want our guts to be filled with a diverse range of mutually beneficial and competitive interactions, a perfect blend of friends, frenemies, and enemies to keep our guts active and body on its toes. Read how networks can help understand these interactions!
Have you ever found yourself less popular when compared to your friends? Interestingly, in any group of individuals, on average, people have fewer friends than their friends do, or at the very most, an equal number. Not more!
Together with Arnaud Bom from Analytic Storytelling, we decided to promote some of the articles on the Network Pages because of the creative writing techniques the authors used. We want to share these writing tips with you so that you can apply them in your writings!
In this article, dear reader, I am going to show you in which way the development of your opinion during the last political issue, the spread of a virus among your acquaintances during the current pandemic, and the alignment of some particles lying inside the device from which you are reading this article are extremely comparable phenomena.
In this article, we will discuss a mathematical riddle that "seems impossible even if you know the answer". It is better known as the 100 prisoners problem.
-waves. Some diseases like epilepsy are thought to be related to ``over-synchronization'' of the brain. Hence synchronization is not always beneficial.
