Science in the city

Topics Art

In the city of Utrecht there are four wall paintings of Dutch physisists. Do you know which ones?

In this short blog post we want to take you on a virtual bike ride in the city of Utrecht. In various neighborhoods of the city you can find beautiful wall paintings, among which four paintings of Dutch physisists. These four paintings were created as part of the project "Mural paintings", started by Utrecht physicists Sander Kempkes and Ingmar Swart, along with the artist collective De Strakke Hand.

Caroline Bleeker produces the phase contrast microscope

On the website of Utrecht University we read:

"Caroline Bleeker developed the phase contrast microscope together with University of Groningen Professor and Nobel Prize winner Frits Zernike. They received a patent for their invention in 1947. The phase contrast microscope makes it possible to see the interior structure of living cells, allowing researchers to follow the process of cell division in living bacteria, for example."

Where to see: Strosteeg 4B.

You can read more about Caroline Bleeker's work on the website of Utrecht University.

Prof. Van ‘t Hoff studies Stereochemistry

On the website of Utrecht University we read:

"This mural depicts Jacobus Henricus (Henri) van ‘t Hoff, who started the field of Stereochemistry during his PhD research in Utrecht. Stereochemistry can be described as a kind of ‘spatial chemistry’: the phenomenon that molecules that are composed of the same atoms can be structured in different ways, for example as mirror images of one another."

Where to see: Ganzenmarkt 26.

You can read more about Jacobus H. van 't Hoff's work on the website of Utrecht University.

Professor Buys Ballot investigates the Doppler Effect

On the website of Utrecht University we read:

"This mural painting shows physicist and meteorologist Christophorus Buys Ballot (1817-1890) who proved the existence of the Doppler Effect. The Doppler Effect is a phenomenon that occurs when objects emit waves, for example light or sound. If you observe these waves while the source moves, or if you are moving while observing the waves, it looks or sounds like these waves have a different wavelength. Sound becomes more high- or low-pitched."

Where to see: Burgemeester Reigerstraat 9, you can see it clearly from the train tracks near the station Maliebaan.

You can read more about Christophorus Buys Ballot's work on the website of Utrecht University.

Leonard Ornstein investigates the random walk

On the website of Utrecht University we read:

"This mural painting shows the drunkard walk, an example of the random walk professor Leonard Ornstein (1880-1941) investigated. You can visit this mural at Oosterkade 30 in Utrecht. The random walk is a series of random consecutive steps an object can make. This theory is used to create models for predictions, like stock prices or how a floating object moves across the water."

Where to see: Oosterkade 30, you can see it clearly from the train tracks near the station Vaartse Rijn.

You can read more about Leonard Ornstein's work on the website of Utrecht University.

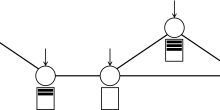
The stochastic process of professor Ornstein

This was a nice virual ride in the city of Utrecht and we hope you enjoyed it, but the actual goal of this short post was to lure you into a little bit of math. We want in the follow up to describe in more detail what the "Ornstein-Uhlenbeck stochastic process" is, named after Leonard Ornstein and George Eugene Uhlenbeck. It is a very elegant and simple mathematical construction with applications in financial mathematics and the physical sciences.

Its original application in physics was as a model for the velocity of a massive Brownian particle under the influence of friction. This is the formula depicted on the fourth wall painting. And the name "Toevalsbeweging" means in Dutch "Random Movement" (Dutch people love gluing words together). In the follow up we explain what professor's Ornstein's notorious formula

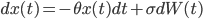
$dx(t) = -\theta x(t)dt + \sigma dW(t)$

represents. Consider a particle with radius 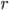$r$ (the Brownian particle) immersed in a fluid of much smaller particles (atoms). The agitated motion of the large particle is much slower than that of the atoms and is the result of random and rapid collisions due to density fluctuations in the fluid. The goal is to find a way to calculate the position 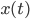$x(t)$ of the particle at time $t$ .

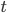Although it seems as a very complex type of system with a tremendous amount of collisions, which change the velocity and direction of the particle, we can still reason as in classical Newtonian mechanics. Newton's second law of motion states that the derivative of the velocity at time 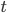$t$ , i.e. 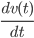$\frac{dv(t)}{dt}$ , should be equal to the force 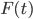$F(t)$ exercised on the particle at that time. Hence

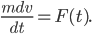
$\frac{m dv}{dt} = F(t).$

This force $F$ is due to the interaction of the Brownian particle with the surrounding medium. If the p0ssitions of the moelcules in the surrounding medium are known as a function of time, then in principle this force is a known function of time. But as you can imagine, in practise, it is unfeasible to derive an exact mathematical formula for the force $F(t)$ , for each time 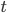$t$ . This is because of the many collusions that occur with the particles in the medium which are in some sense "random".

From experience we know that in typical cases this force is dominated by a friction force 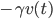$-\gamma v(t)$ , where the friction coefficient 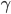$\gamma$ is in general a known quantity. Hence we obtain the equation

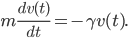
$m\frac{dv(t)}{dt} = -\gamma v(t).$

or equivalently

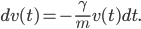
$dv(t) = -\frac{\gamma}{m} v(t)dt.$

Since the particle is moving in a fluid, we may also expect some random density fluctuations in this fluid. In many cases we describe such random density fluctuations using the Wiener process 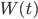$W(t)$ , where the variance of these random fluctuations is given by a coefficient 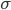$\sigma$ . Hence we obtain the formula

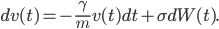
$dv(t) = -\frac{\gamma}{m} v(t)dt + \sigma dW(t).$

This looks like the formula in the wall-painting, but not entirely. In the painting the formula gives the position 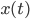$x(t)$ , our formula gives the velocity 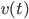$v(t)$ . After some tedious calculus you can solve the above equation and find an expression for the velocity 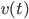$v(t)$ . Afterwards using again Newton's equation

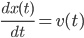
$\frac{dx(t)}{dt} = v(t)$

it can be shown that the psition 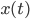$x(t)$ also satisfies an equation of the form

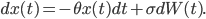
$dx(t) = -\theta x(t)dt + \sigma dW(t).$

where the exact value of 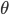$\theta$ follows from the tedious computations mentioned above.

Back to the painting

Go back for a second to the wall-painting with professor Ornstein. Do you notice at the bottom the footsteps? This illustration is another way to think about the Ornstein-Uhlenbeck process described above. Think of a drunken walker trying to follow the straight line in the middle of the street. Of course a drunken walker will definitely fail to do so, but how will the walk look like in the end? Well, it will look like the pattern in the illustration. But what does this have to do with the equation?

You can think of being drunk as a condition that affects your movement in a totally random way, the coefficient 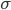$\sigma$ describes how drunk the walker is. The more drunk the walker is, the more random the movember will be and the further the walker will deviate from the white line in the middle. But the walker really wants to walk on the straight line in the middle, hence there is an intrinsic force, call it motivation, or stubbornness, pulling the walker back to the line. All these features come together in this beautiful equation

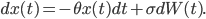
$dx(t) = -\theta x(t)dt + \sigma dW(t).$

How the walker's position changes at time 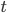$t$ (the term 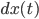$dx(t)$ ) depends on the intrinsic force pulling the walker back to the middle (the term 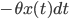$-\theta x(t)dt$ , the further the walker is from the middle the higher this intrinsic force is to return to the middle (this is why 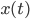$x(t)$ appears again in this term), and also on how drunk the walker is, represented by 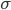$\sigma$ , which makes the walker's legs move in a random direction (i.e. 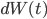$dW(t)$ ). This is some maths about drunken walks!

It seems that mathematicians are really fond of stories with drunken walkers, you may want to have a look also at this story. In any case, if you happen to be in Utrecht one day and you will want to have a nice bike ride, you can choose to ride by these wall paintings and see them in person!

Question for the readers: are you aware of similar initiatives in other places? You can leave a comment below, we will look into it and maybe come back with a story!