In February 2024, the second Volume of the Random Graphs and Complex Networks book series has appeared. While Volume 1 is aimed at master students in mathematics and related fields, Volume 2 is aimed more towards the research community. This community includes PhD students and researchers, with a mathematical background. Having worked on it for some 17 years, it is quite a relief that it has finally appeared in press!
The book covers recent developments in random graphs theory about the local and global structure of random graphs. It is the first book covering the central notion of local convergence, a method that has had profound consequences in random graph theory. Many properties of random graphs can be understood by linking them to the random graph’s local limit.
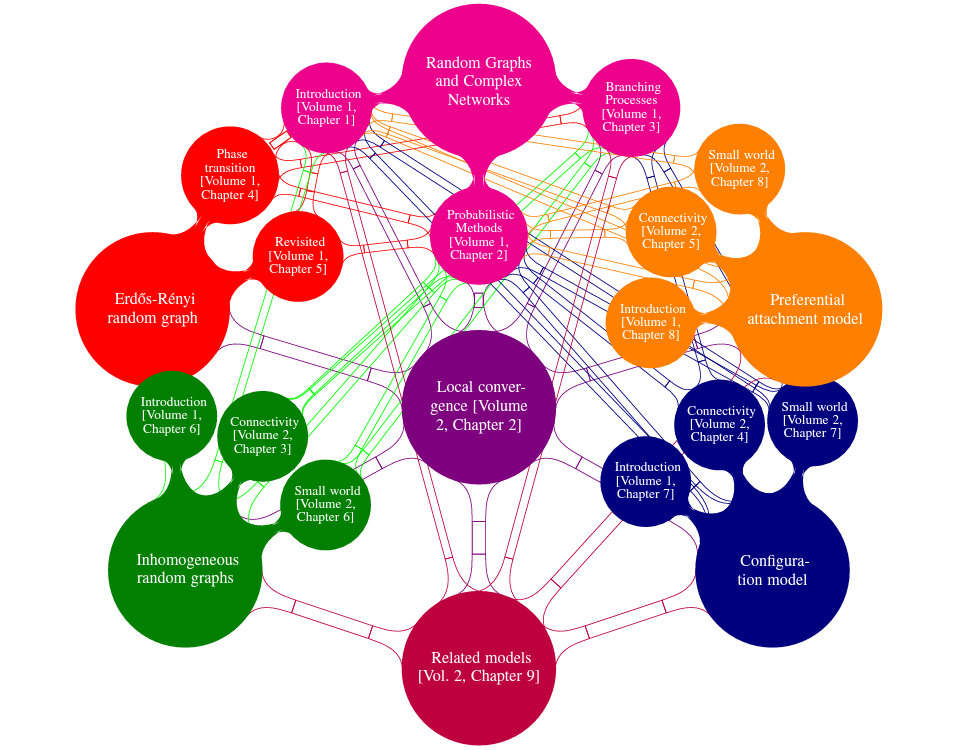
The relation between the chapters in Volumes 1 and 2.
Further, the book covers global properties, such as the existence of a giant connected component containing a positive proportion of the vertices in the graph, as well as when random graphs are fully connected. Another point of focus are the small-world properties of random graphs. The book closes with an extensive discussion on related random graphs models, discussing models that are directed, have a local or global community structure, or have a geometric structure. The book has some 300 exercises that allow readers to sharpen their familiarity with the topics that are discussed. It is online available on my personal website.
A graph consists of objects called vertices and connections between them called edges. For every vertex, we can count how many neighbors it has, which is called its degree.
How are elements in real-world networks connected? That is the question we aim to answer in this post. Most real-world networks turn out to be extremely inhomogeneous.
Social networks are remarkably small, in the sense that you can hop between any two individuals in them using only a few hops. This video explains what such small-world networks are, why social networks are so small.
