Quantum synchronization in complex networks

Synchronization is a phenomenon which has been investigated since a few decades. The phenomenon describes the locking of the frequency of coupled oscillators. The occurrence of synchronization phenomena is overwhelming, a short description of synchronization and some videos can be found here.

Quantum and Classical Synchronization

As many phenomena in the classical world have quantum counter part, it raises the question if this is also true for synchronization. As synchronization is a collective phenomenon, it may help gaining a better understanding of how collective phenomena in the classical and quantum world are connected.

Recent work by Witthaut et al. have recently established a relationship between synchronization and entanglement, and hence between classical and quantum mechanics. Entanglement has been one of the most puzzling and conspicuous phenomena in quantum mechanics. If you have two particles, say A and B, of which one has spin up and another has spin down, they are in an entangled stated when the total state of the system consisting of A and B is not a (tensor)product of the states of A and B.

This statement can be explained as follows.

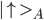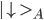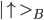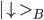Assume particle A has a magnetic moment (identified with the spin of the particle) which can point up or down. We denote the states as $|\uparrow>_A$ or $|\downarrow>_A$ . The same is true for particle B, which is in states $|\uparrow>_B$ or $|\downarrow>_B$ . Therefore the system consisting of A and B particles can be in any linear combination of products of A and B-states. One of the best known entangled states are the Bell-states of which

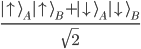
$\frac{|\uparrow\rangle_A|\uparrow\rangle_B+|\downarrow\rangle_A|\downarrow\rangle_B}{\sqrt{2}}$

is a typical example.

Similar superposition states can be made for a large collection of particles leading to so-called entangled number states; typically light is used for creating such states, but they also exist in collections of ultracold atoms. Light considered as a wave has both an amplitude and a phase. Just like the position and the speed of a particle obey the Heisenberg uncertainty relation, the phase and the amplitude of the light wave obey an equivalent uncertainty relation:

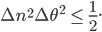
$\Delta n^2\Delta \theta^2\, {\leq}\,\frac{1}{2}.$

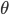Here $n$ denotes the number of excitations (photons in the case of light) in the wave, which is a measure of the wave amplitude and $\theta$ is the phase of the wave. If we can saturate the inequality and make 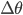$\Delta \theta$ sufficiently small we get non-classical so-called phase squeezed state. The squeezing parameter 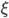$\xi$ quantifies to which extent the state is squeezed. Moreover, it can be shown that there is a direct relation between the squeezing parameter 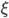$\xi$ and so-called number entanglement:

if 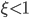$\xi<1$ the quantum system is number entangled, that is, the number fluctuations of the quantum state exceed the maximum possible for a non-entangled state, and hence the system shows quantum behavior. In the case $\xi\gg 1$, the number fluctuations do not exceed the maximum for a non-entangled state and hence we are in the classical regime.

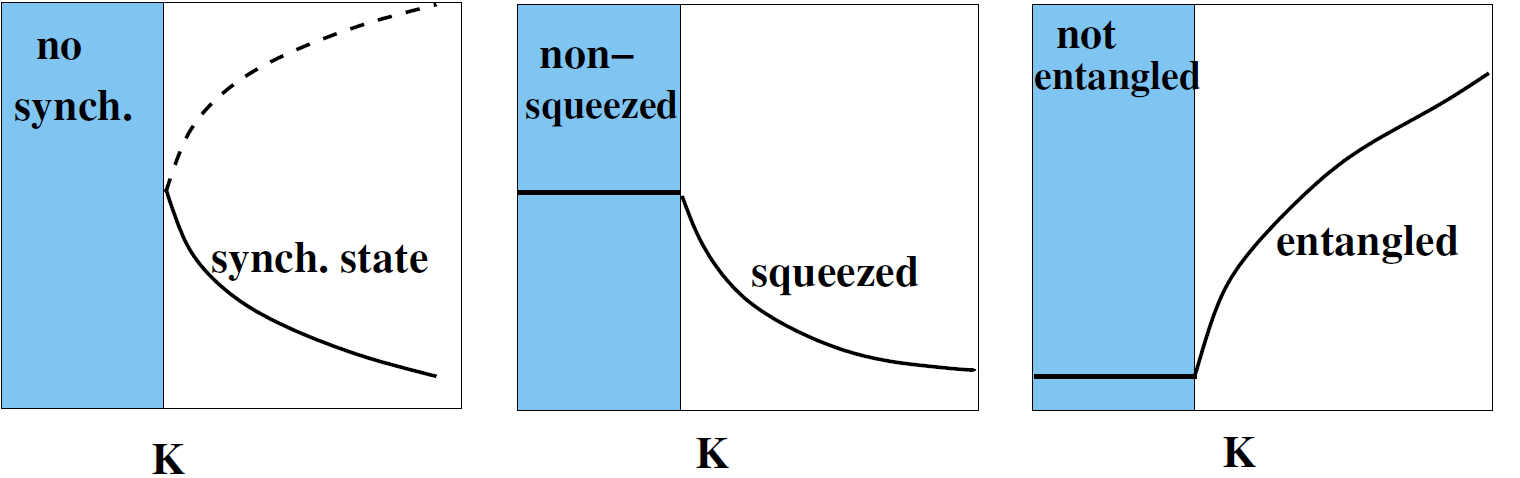
Figure 1 below shows that there are striking resemblances between the squeezing, entanglement and synchronization transition and that they occur at the same value of the coupling parameter 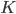$K$ .

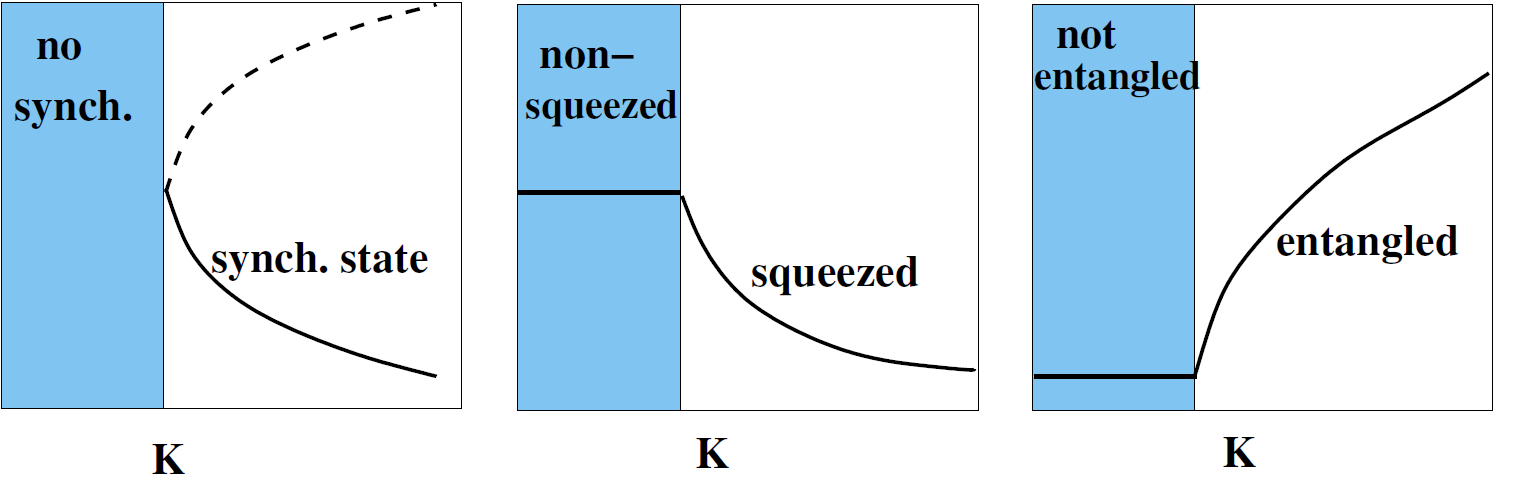
Graphics redrawn from this article in Nature.

It is even more striking that the equations for the quantum system reduce (in the mean-field limit) to the same equations that underlie the most used model of synchronization: the Kuramoto model in which many oscillators are coupled in a particular way, namely as a sinusoidal function of the phase differences:

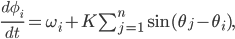
$\frac{d\phi_i}{dt}=\omega_i+K \sum_{j=1}^n\sin(\theta_j-\theta_i),$

with 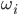$\omega_i$ the natural frequency of oscillator 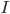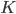$I$ , $K$ is the coupling constant and $n$ is the number of oscillators.

This model has been widely studied and it is favoured by mathematicians, see for example work by Frank den Hollander (Leiden University), and physicists as an analytical solution exists in certain cases.

The way Kuramoto solved it was by guessing the solution. Proving the stability of the stable synchronous state has kept mathematicians busy for a number of years until Steven Strogatz proved that stability can be demonstrated using Landau damping techniques.

The finding that this classical analysis applies to quantum many body systems such ultracold atoms is a surprise that forms another connection between the quantum and the classical world.

In a following article we turn to the future, when the internet will have turned quantum and see in what way synchronization is important there.

Conclusion

The body-clock is a complex network of neurons that is difficult to model mathematically, due to its many intricacies. Above we have seen that we can gain some understanding by using mathematics and simulations, but also that experiments uncovering an interesting phenomenon can play an important role in guiding mathematicians in making choices about which questions are interesting and worthwhile to study.

Specifically, we have found a possible mechanism for the different types of transitions to the phase-split state observed in experiments. Which transition occurs will depend on the interactions strengths, which may be different in different individuals. Much remains to be done in studying the two-community Kuramoto model, and even more when it comes to understanding the body-clock.

Would you like to stay up to date when a new post appears on the Network Pages?

Subscribe to our mailing list