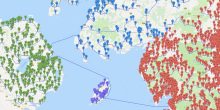
Measures to halt the spread of Covid-19 are having an enormous impact on the cultural sector. In some cases mathematics turns out to be very helpful.
Cinema’s, theatres, expositions, life-shows have been changed in an almost unimaginable way. Coping with distance rules on the one hand, and surviving commercially on the other hand is an enormous challenge for businesses in this sector.
Figure 1: Upper- and front view of chairs in the Music Building Eindhoven.
In the last half year a number of creative ideas has been developed. One basic starting point is to fill the theatre to the maximum given the existing distance rules. Mathematical models, and their solutions, can help in achieving this objective.
In this article we show how we have applied such models to the Music Building Eindhoven. Our conclusion in a nutshell is as follows: when allowing two shows per evening, it is possible to find solutions that use approximately 70% of the capacity. In these solutions, no pair of visitors from different families is seated within 1.5 meter, and no seat is used twice during a single evening.
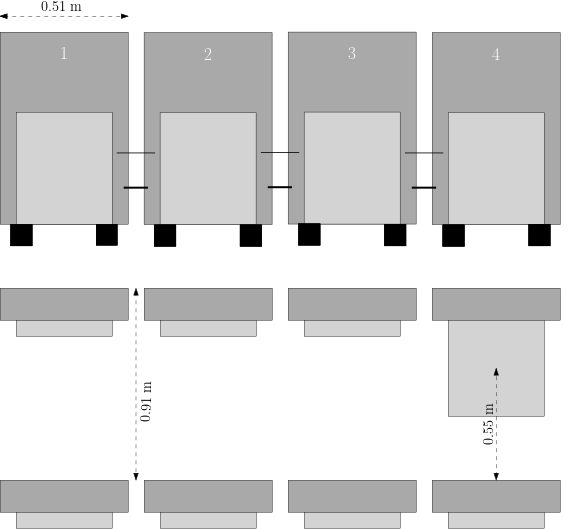
We now focus on the models and methods that are being used by the MBE (see Figure 1). MBE has two rooms: the Small Room (400 seats) and the Grand Room (1250 seats). Since members of the same family are allowed to sit next to each other, it is important how many families, of what size, intend to visit the show (the size of a family is its number of members). We can obtain this information from historical data from the MBE. So we can assume that we know, with great precision, how many families have size 1, size 2, size 3 and size 4; we call this information about the sizes of the families a profile.
Figure 2: By placing (virtually) non-overlapping trapezoids over the seats, we can guarantee that persons belonging to different families sit far enough apart. Green seats are occupied by members of a same family; red seats remain empty.
A fundamental concept in our model is a trapezoid: a quadrilateral with at least two opposite sides that are parallel. We can prove that an assignment of families to seats corresponds to placing trapezoids that are pairwise disjoint (see Figure 2). Indeed, each trapezoid allows to seat family members within the “centre” of the trapezoid; it is a consequence of a trapezoid packing that members of different families are separated by at least 1.5 meter.
Thus, the resulting optimization problem is to place as many, pairwise disjoint, trapezoids, each trapezoid being weighted by the size of the corresponding family; we model this using a mathematical technique called integer programming. The result is an integer programming problem which we can solve. Given a profile, the objective in this model corresponds to allowing as many visitors as possible, while satisfying the constraints that trapezoids are pairwise disjoint, and that each seat is used at most once in case of multiple shows per evening . If you click on the drop-down menu below you can see this integer programming problem, it may seem complicated but it is possible to solve it. For an explanation of the model, and the corresponding algorithms we use to solve it, we refer to [1].
Figure 3: The “trapezoid model” formulated as integer programming problem.
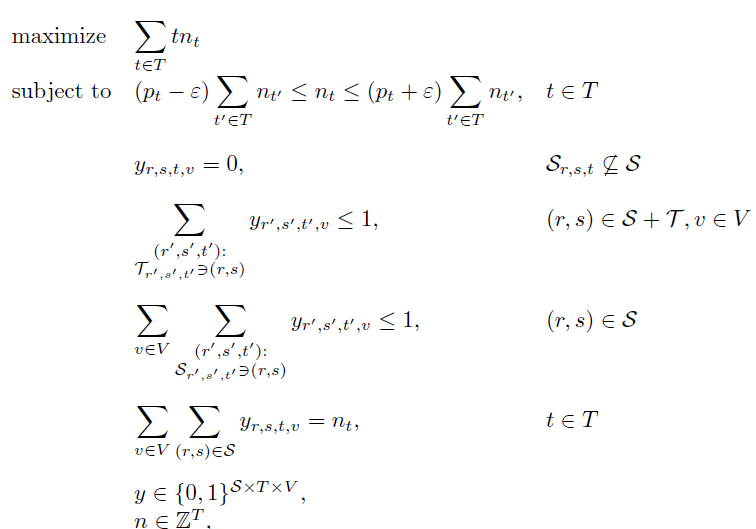
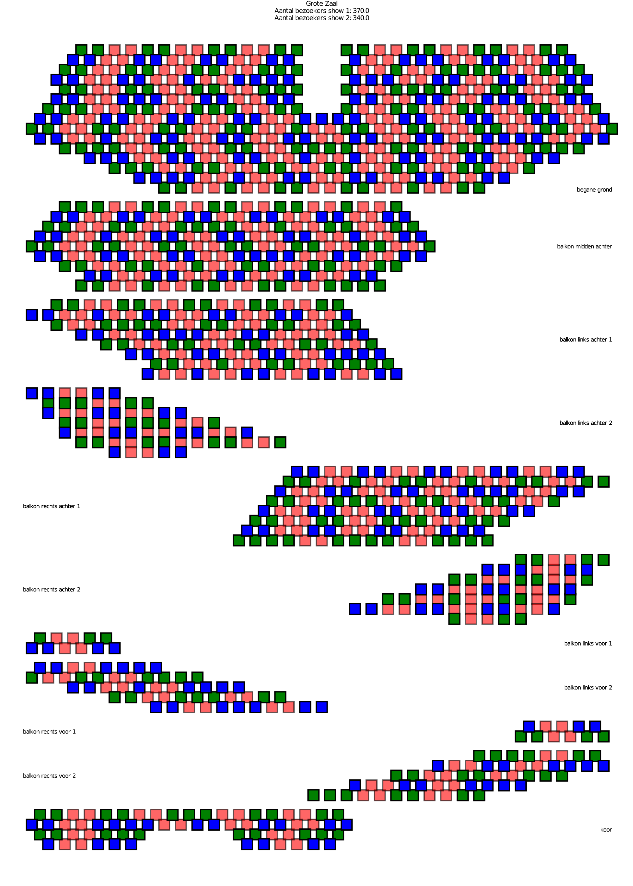
Solutions of this model reveal that when allowing only a single show per evening, the number of visitors will not exceed 1/3 of the capacity for any realistic profile. However, when two shows per evening are allowed, it is possible to reach almost 70% of the seat-capacity. Figure 4 illustrates such an optimal solution for the Grand Room based on a profile coming from historical data.
Figure 4: Illustration of seating assignments for consecutive shows. A green square corresponds to seat used in show 1, while a blue square corresponds to seat used in show 2, and a red square corresponds to a not-used seat.
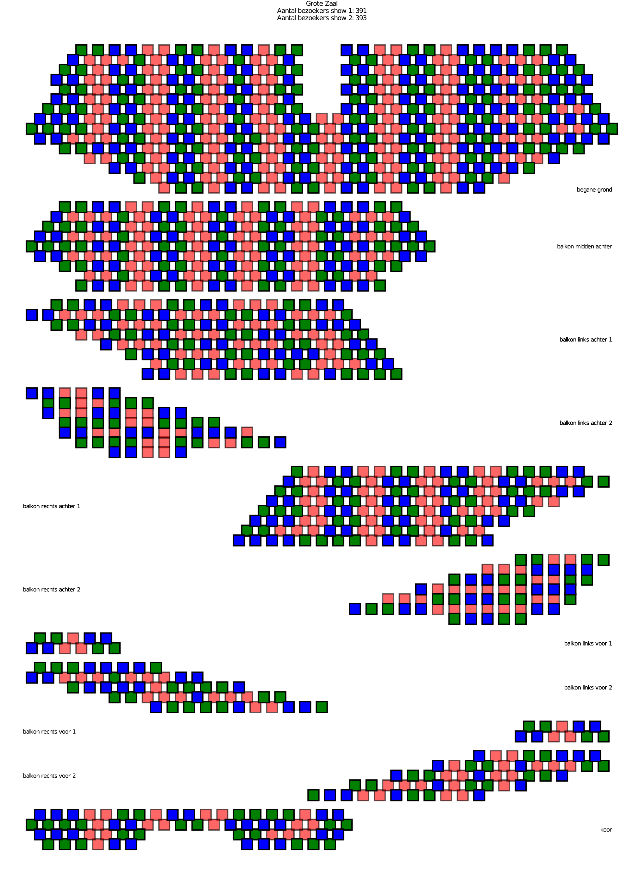
In practice, many theatres use solutions in which rows of seats are used alternately, i.e., all seats in the even rows are empty, and occupied seats are only present in the odd rows. Indeed, from a logistical point of view such a solution has advantages: it is much easier to guide visitors to their appropriate place. In order to assess the impact of having this property in a seating assignment, we solved the model with the requirement of this alternate property. It appears that this reduces the number of visitors with less than 10%, see Figure 5 for an illustration of a resulting solution.
Figure 5: Illustration of seating assignments for consecutive shows. A green square corresponds to seat used in show 1, while a blue square corresponds to seat used in show 2, and a red square corresponds to a not-used seat. If you look closely you will see that even rows have only blue seats while oneven rows only green seats.
We conclude by observing that traditional mathematical optimization techniques can help in (i) finding optimum seating assignments, and (ii) assessing the impact of particular demands on the reachable capacity.
During my studies in mathematics, I never thought about how I should practice or learn mathematics. Have you ever thought about this? I was learning formulas, theorems, proofs, and various other results by hard and applying them in new situations. Now I realize I could have approached it differently.
Recently there has been a breakthrough in the field of algorithms for geometric network problems, concerning the complexity of the Euclidean Travelling Salesman Problem.
A conjecture of Erdős and Hajnal from 1989 says that forbidding any specific substructure results in existence of a very large homogeneous one! In this article you will have a look into one of the most fascinating problems in modern graph theory.
