Creativity is intelligence – The Network Pages

While growing up, even during my studies in mathematics, I never thought about how I should practice or learn mathematics. Have you ever thought about this yourself? I was learning formulas, theorems, proofs, and various other results by hard and applying them in new situations. By spending many hours and much energy in this I managed to finish my undergraduate studies in mathematics. Maybe I should have thought of this question much earlier, it would have changed the way I see mathematics.

I started thinking about creativity in mathematics when I was reading the book "Proofs from the Book", by Martin Aigner, Günter M. Ziegler. This is one of the nicest mathematics books I have ever read. It contains mathematical problems which have a short, elegant, and surprising proof. I totally recommend it! Some of them are quite advanced, but definitely worth reading. Each chapter discusses a different mathematical problem, from geometry, combinatorics, number theory, or analysis. But the proofs given are very surprising. For example, a problem from graph theory can be proved using techniques from topology. The proofs have something magical, they create feelings of amazement but also doubt whether you would be able to ever think of something so smart on your own. When I discussed these thoughts with friends, colleagues, and students we came to two conclusions.

First of all, when you explain the solution of a problem to someone, you usually don't devote time to discuss the whole creative process of coming up with that solution. We often tend to explain a solution as a sequence of correct and logical steps. Of course after a clear explanation of these steps everyone believes the correctness of the result. In the end, the problem loses its status as a difficult problem since its solution seems rather simple. The one explaining goes home with a nice feeling of success since they offered a very clear explanation. At the same time, those in the audience go home full with confidence that they understood all the steps. They sit down to solve another problem, and rather quickly realize that doing it yourself is a totally different story than listeting to someone explain it.

It is the same with many things right? You watch the world rowing championship on tv and you think

"Well, she makes it look very easy to row in the single sculls!"

Then you go and you try to row in the single yourself, and you flip over in the water! Same with mathematics. The difference with math is that when we can't solve a problem ourselves, we also have to deal with the societal image of mathematics, summarized as "I can't do it, I don't like mathematics, I am not smart enough". I hope you see the sad difference in approaching these two rather similar phenomena.

To go back to that discussion I had with my colleagues and students. We also reached a second conclusion. We should always keep in mind that a surprising solution to a mathematical problem, that often feels like magic, was probably the result of months of hard work and experimenting with various mathematical techniques, until the author finally came up with one proof that does the job.

Like a nice of piece of music, the composer didn't come up with it at once in one day. There are months of trying and failing behind it. When explaining mathematics I try my best to also show how I do mathematics. Sometimes we just apply definitions to develop some skills, other times we need to sit down a couple of hours and try out various things until we find a clue. But staring at a piece of paper until our neurons pop up a solution, is not how mathematicians work.

About creative proofs

Mathematics is a science relying on creativity. Let me give an example showcasing this. The book I talked about before (Proofs from the Book) has a chapter that talks about Kneser's conjecture, which was an open problem related to sets. László Lovász, an Abel prize laureate, came up with a proof by solving a similar problem about graphs. It is fascinating that his proof is not complicated and lengthy, filled with technical language that only experts can understand. Rather, he presented an elegant proof by using a theorem from topology, called the Borsuk-Ulam theorem. I recommend reading an article about this theorem written by Yilin Li, as it showcases another impressive and creative application of it.

The Borsuk-Ulam theorem

The Borsuk-Ulam theorem says that if $f : \mathbb{S}^n \rightarrow \mathbb{R}^n$ is continuous, then there exists a point $x\in \mathbb{S}^n$ such that $f(-x) = f(x)$ .

Don't feel intimidated by the formal statement. When we write $\mathbb{R}^n$ we mean the set of $n$ -dimensional vectors of real numbers, i.e.

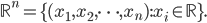
$\mathbb{R}^n = \{(x_1,x_2,\dots,x_n): x_i \in \mathbb{R}\}.$

With $\mathbb{S}^n$ we mean a sphere as you know it, but in $n$ dimensions, $\mathbb{S}^1$ is just the circle, $\mathbb{S}^2$ is the "ordinary" sphere. The formal definition is

$\mathbb{S}^n = \{ x \in \mathbb{R}^n \text{ such that } x_1^2+x_2^2+\dots+x_n^2 =1\}.$

In other words, every continuous function from an $n$ -dimensional sphere to the real vectors always maps some pair of antipodal points to the same number. Antipodal points are in exactly opposite directions form the sphere’s center.

Such proofs show clearly that mathematics is a science where creativity is the main ingrediend. Of course, it needs work and time to develop the necessary tools to solve problems, but in the end, the most interesting process is that of experimenting with various concrete examples to gain an understanding of the concepts or problems at hand. This leads the way to a solution. And in most cases creativity is necessary.

To summarize, my view on how to practice mathematics has switched drastically in the last years. Thinking about a problem is more a question of understanding and creativity. Experimenting with mathematics is where the fun is, figuring out the solution is the reward for all the hard work trying to understand what is going on. I think that mathematicians should and could show more how it is to do mathematics, than just explaining the results they prove!

The featured image was taken from this amazing video from Numberphile. You can also watch this very nice video from 3blue1brown on the necklace splitting problem and the Borsuk-Ulam theorem.

Would you like to stay up to date when a new post appears on the Network Pages?

Subscribe to our mailing list