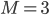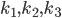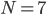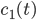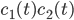Chemical reactions evolve in the same way as water flows through a network of rivers. When describing a chemical reaction you can imagine that the concentrations of the reactants are flowing through the reaction network in the same way as water flows through the network of rivers. Kinetic models describe how the concentrations flow through the states of the molecular species in the network.
In the preceding article we discussed how one can construct a reaction network describing the reactions occurring in a chemical system. Reaction networks are a useful tool when we want to describe complex reaction mechanisms. Such reaction mechanisms often involve numerous intermediate and product molecular species. The molecular graph of a reactant is gradually transformed into the graph of a product by following some predefined reaction steps. The reaction network allows experts to explore various reaction pathways in great detail. In this article we will focus on how to reconstruct a kinetic model from the reaction network.
To start with, suppose we have a reaction mechanism that involves several steps and consider the corresponding reaction network. Such a mechanism is illustrated in Figure 1 below.
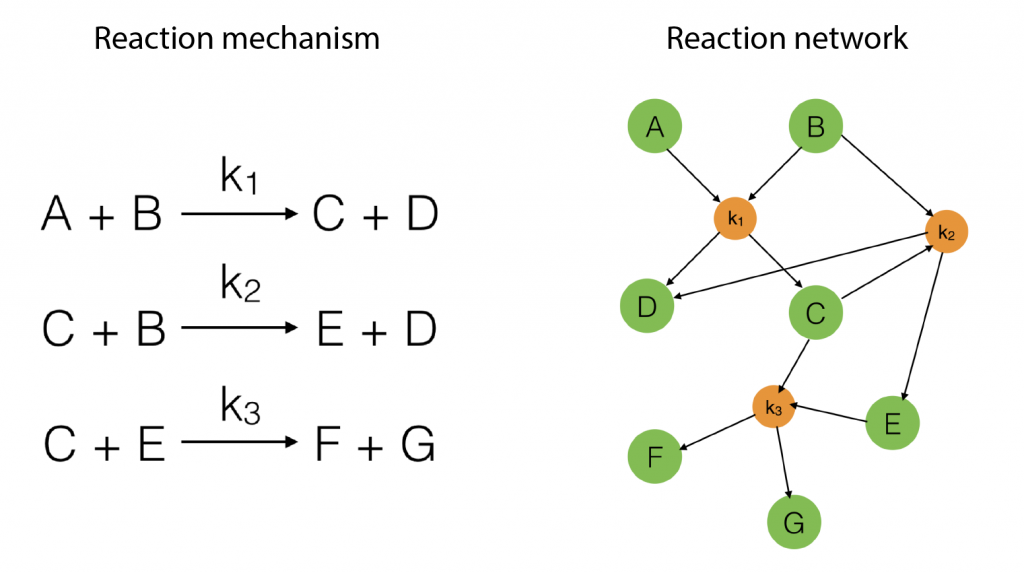
Figure 1: An example of a simple reaction mechanism
Kinetic Model
A kinetic model is a system of ordinary differential equations that describes how the concentrations of molecular species taking part in the reaction mechanism are changing in time. The equations in the kinetic model are constructed in terms of reaction rates. Intuitively, the reaction rate describes how often the reaction happens and which molecular species are the reactants. Reaction rates depend in general on the concentration of the reactant species and on the conditions in which the reaction happens (temperature, pressure, volume).
With no doubles, the kinetic model is the central idea in the studies of co-occurring chemical reactions, it is basically a dynamical system that tells us how the concentrations of chemical species evolve in time. This dynamical system may involve many equations, but it is typically very ‘sparse': only few variables per one equation. Chemists like represent this sparse structure by a network. The properties of the dynamical system can then be mapped to the topological peculiarities of this reaction network.
says dr. Ivan Kryven, from the van 't Hoff Institute for Molecular Sciences, University of Amsterdam.
Lets see an example, suppose we have two reactants, denoted by 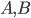 and that
and that 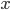 molecules of
molecules of 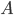 react with
react with 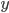 molecules of
molecules of 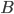 to yield the two products
to yield the two products 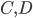 . Schematically this is depicted as follows:
. Schematically this is depicted as follows:
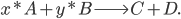
Then the rate of this reaction is
![Rate = k*[A]^x*[B]^y,](https://www.networkpages.nl/wp-content/plugins/latex/cache/tex_a662c31683bfebe73e9609c673fb0d2d.gif)
where  is some coefficient. In this equation,
is some coefficient. In this equation, ![[A], [B]](https://www.networkpages.nl/wp-content/plugins/latex/cache/tex_03447f154f66f43e99444bfe4717ea76.gif) are the concentrations of the corresponding molecular species and their product determines the probability that they find each other and react. The higher the concentrations, the easier for the molecules to collide. The exponents
are the concentrations of the corresponding molecular species and their product determines the probability that they find each other and react. The higher the concentrations, the easier for the molecules to collide. The exponents  specify how many molecules of each reactant are needed for the reaction to happen. The example above requires
specify how many molecules of each reactant are needed for the reaction to happen. The example above requires 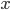 molecules of
molecules of 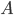 and
and 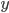 molecules of
molecules of 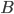 . The value of
. The value of  gives an overall order of a reaction: the total number of reactant molecules. The most common reactions are of the first and the second order: they happen with one or two molecules. The first or the second order reactions are also called unimolecular or bimolecular, respectively. The coefficient
gives an overall order of a reaction: the total number of reactant molecules. The most common reactions are of the first and the second order: they happen with one or two molecules. The first or the second order reactions are also called unimolecular or bimolecular, respectively. The coefficient  , called the rate coefficient, includes the information about the conditions in which reaction happens (temperature, pressure, etc). Rate coefficients are usually obtained from the experiments or from quantum chemical calculations, these details are omitted from the article and we suppose that the values of
, called the rate coefficient, includes the information about the conditions in which reaction happens (temperature, pressure, etc). Rate coefficients are usually obtained from the experiments or from quantum chemical calculations, these details are omitted from the article and we suppose that the values of  are known for the considered reactions.
are known for the considered reactions.
The main motivating question leading to kinetic models rises. How do the concentrations of the various molecular species change given the rates of the reactions? Suppose we have a reaction mechanism where 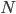 molecular species take part. Then we would like to know what the concentration of each one of them is at a given time
molecular species take part. Then we would like to know what the concentration of each one of them is at a given time 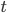 , these concentrations will be denoted by
, these concentrations will be denoted by 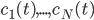 . The left hand side of each equation in the kinetic model is the partial derivative of a concentration of a particular molecular species with respect to time,
. The left hand side of each equation in the kinetic model is the partial derivative of a concentration of a particular molecular species with respect to time, 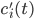 ,
, 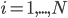 . This describes the speed at which the concentrations change in time. On the right hand side we relate the changes in the concentrations to the rates of the various reactions. This leads to equations of the following form:
. This describes the speed at which the concentrations change in time. On the right hand side we relate the changes in the concentrations to the rates of the various reactions. This leads to equations of the following form:
\begin{equation}\label{eqn:concentrations}c_i'(t) = \sum _{j} P_j - \sum_{m} R_m. \end{equation}
In order to understand these equations we note that, when measuring the concentration of a given molecular species during a chemical reaction, there are reactions that will increase its concentration (produce this species) and reactions that will decrease its concentration (consume this species).
The positive contributions 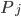 come from rates of reactions that include
come from rates of reactions that include 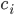 as a product (the reactions that produce this species). The negative term includes all the rates of reactions
as a product (the reactions that produce this species). The negative term includes all the rates of reactions 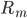 where the
where the 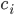 plays a role of a reactant (it undergoes a transformation and its concentration decreases)!
plays a role of a reactant (it undergoes a transformation and its concentration decreases)!
Usually kinetic models are constructed manually. The problem comes when the reaction mechanism is too big and constructing a kinetic model requires a lot of effort and attention. Then, the question is: how to transform the information from the reaction network to the kinetic model?
The reaction network can be described by the adjacency matrix 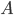 of size
of size 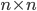 , where
, where 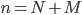 . Here
. Here 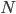 represents the number of molecular species and
represents the number of molecular species and 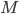 the number of reactions.
the number of reactions. 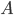 has two types of nodes, nodes corresponding to:
has two types of nodes, nodes corresponding to:
- molecular species
- and reactions.
Nodes corresponding to molecular species have a weight corresponding to their initial concentration, denoted by 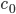 . The weight of a node corresponding to a reaction denotes the rate coefficient
. The weight of a node corresponding to a reaction denotes the rate coefficient  of the corresponding reaction.
of the corresponding reaction.
The rate equation for each state of the molecule is reconstructed by exploring its neighborhood in the reaction network. The incoming edges denote the reaction pathways that contribute to the concentration of the species considered while the outgoing edges denote the reaction pathways that lead to a decrease in the concentration of the species considered.
In what follows we are going to describe the formal transition from the reaction network to the reaction rate equations. We will only consider reactions of first and second order, and their mixtures, as most of the reaction mechanisms involve mixtures of the first and second order reactions. For this purpose, we will use three main components:
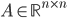 - adjacency matrix of the reaction network,
- adjacency matrix of the reaction network,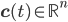 - vector of concentrations of each molecular species and
- vector of concentrations of each molecular species and - vector of rate coefficients for each reaction from the reaction network.
- vector of rate coefficients for each reaction from the reaction network.
The entries of 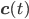 that correspond to the reaction nodes in the adjacency matrix and the entries of
that correspond to the reaction nodes in the adjacency matrix and the entries of 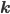 that correspond to the species nodes in the adjacency matrix are zero. The shape of all these quantities is illustrated in Figure 2 below.
that correspond to the species nodes in the adjacency matrix are zero. The shape of all these quantities is illustrated in Figure 2 below.

Figure 2: An adjacency matrix, concentration vector and coefficient vector of a simple second order reaction networks introduced in Figure 1
First order reactions
We consider first the case of a reaction mechanism that consists of only first order reactions. For a state node 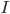 , the differential equation describing the distribution of species concentration
, the differential equation describing the distribution of species concentration 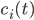 is written in terms of the adjacency matrix of the reaction network
is written in terms of the adjacency matrix of the reaction network 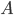 and coefficient vector
and coefficient vector 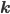 ,
,
\begin{equation}\label{eqn:secondform1}c_i'(t)=\sum_{j=1}^{n}k_{j}(A_{j,i} -A_{i,j})\sum_{l=1}^n A_{l,j} c_l(t).\end{equation}
The difference 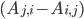 determines the sign of the term: a positive sign means that the concentration of the molecular species increases, a negative sign that it decreases! The equation in \eqref{eqn:secondform1} conveys exactly the same information as equation \eqref{eqn:concentrations}, it is just written in terms of the reaction network!
determines the sign of the term: a positive sign means that the concentration of the molecular species increases, a negative sign that it decreases! The equation in \eqref{eqn:secondform1} conveys exactly the same information as equation \eqref{eqn:concentrations}, it is just written in terms of the reaction network!
Second order reactions
The differential equation given above for 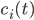 can be extended to cover reactions of the second order, then it takes the form
can be extended to cover reactions of the second order, then it takes the form
\begin{equation}\label{eqn:secondorder}c_i'(t) = \sum_{j=1}^{n} k_j(A_{j,i} -A_{i,j})\prod_{l=1}^{n} c_l(t)^{A_{l,j}}.\end{equation}
The product sign in the last part of the equation accounts for the number of reactants in the reaction.
Exercise: Write the equations in \eqref{eqn:secondorder} explicitly for the reaction described in Figure 1 (use the matrix representation in Figure 2). Interpret these equations!
Mix of first and second order reactions
Let us split the vector of rate coefficients 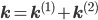 , where
, where 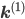 is non-zero for first order reactions and
is non-zero for first order reactions and 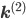 is non-zero for second order reactions.
is non-zero for second order reactions.
A combination of equations \eqref{eqn:secondform1} and \eqref{eqn:secondorder}, together with the corresponding rate vectors 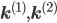 yields the differential equation for a mixed reaction network,
yields the differential equation for a mixed reaction network,
\begin{equation}\label{eq:mixed}c_i'(t) = \sum_{j=1}^{n} k_j^{(1)}(A_{j,i} -A_{i,j})\sum_{l=1}^{n} A_{l,j} c_l + \sum_{j=1}^{n} k_j^{(2)}(A_{j,i} -A_{i,j})\prod_{l=1}^{n} c_l^{A_{l,j}}. \end{equation}
We can solve the system of equations in \eqref{eq:mixed} numerically, this provides us the information about the distribution of the concentrations of all species present in the resulting reaction network. In the end, one might be interested in tracking the cumulative amount of concentration of various functional groups rather than specific molecular structures. This can be done by lumping the concentrations of all the species according to the functional groups they contain. As it was discussed in the preceding article, functional groups are defined as patterns on molecules. By doing so, one can observe the global picture of the chemical process and compare the results to the experimental data, that are usually reported in terms of distributions of various functional groups.
To summarize, in this article we have introduced the systematic way of reconstructing the reaction network into the kinetic model of the chemical process. The kinetic model describes how the concentrations of molecular species travel in time from one state of the reaction network to another. Solving the kinetic model allows to validate the result by comparing the distribution of various functional groups in time with the kinetic data from the experiments. This way of dealing with the complex chemical systems is quite generic and allows to explore them in a great detail.