Have you ever thought about a relation between chemistry and networks? Already from school courses we get the feeling that there is some interplay between mathematics and chemistry. For example, looking at the structural formula of a molecule one immediately observes it is nothing more than a graph! In this article we will see how graph theory can help us understand the way chemical reactions occur.
Figure 1: Molecule of hexanal.
Atoms are connected with bonds in a molecule as nodes are connected with edges in a graph. So it feels very natural to investigate whether the very rich field of graph theory can be used in this context. In a more formal language, we represent molecules using molecular graphs. This mathematical formalism helps scientists understand how chemical reactions evolve. Lets see step by step how this works.
First we need to define a molecular graph. A molecular graph is a graph with labeled nodes and edges. The nodes represent atoms and their labels correspond to the names of chemical compounds. The edges represent bonds between atoms and their labels define a bond order (single bond, double bond, etc.). Furthermore, we use the notation of a self-loop to indicate a radical atom: an atom with unpaired valence electrons. Thus, a molecule is defined by its list of atoms and an adjacency matrix that captures the connectivity between atoms. Unlike a chemical formula, the molecular graph contains explicit structural information of a molecule and can be analysed by a computer just as any other mathematical object. In some sense we can now "program chemistry". For example, the molecular graph representation of an isobutylene structural formula is illustrated in the figure below.
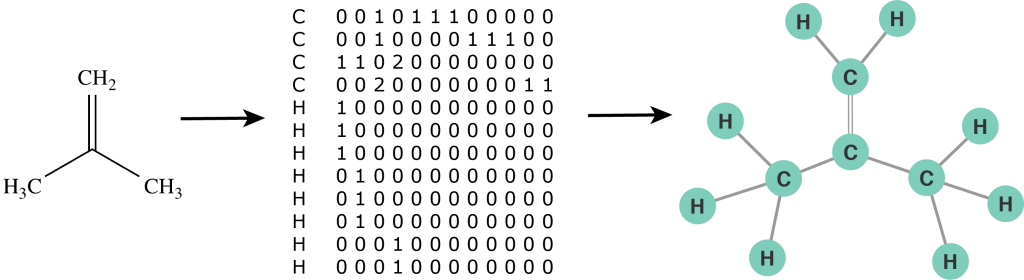
Figure 2: The molecular graph of an isobutylene molecule.
The second step is to consider a chemical reaction. Roughly speaking, in a chemical reaction a reactant undergoes a transformation leading to a product. When a reaction happens the structure of the reactant molecule changes into the structure of the product molecule. Usually a reaction mechanism consists of several intermediate steps, before the final product is obtained. A crucial observation is that an elementary reaction step does not influence the whole molecule, it is applied only to a specific reactive site of it. This fact plays an important role when a molecule is big in size. Only one reactive site of the molecule, that consists of several atoms, takes part in a reaction and undergoes changes, while the rest of the molecule remains unchanged or follows another reaction pathway. From now on, we characterize molecules by their reactive sites and let all of them undergo transformations independently from each other. Using molecular graphs we can fully characterize all the intermediate reaction steps taking place while following a reaction mechanism. A reactive site of a molecule is represented by a subgraph of the corresponding molecular graph, we call it a pattern. In this way, a chemical reaction can be seen as a rule that transforms a pattern of a reactant molecule into a pattern of a product molecule. A reaction rule defined in terms of patterns is illustrated in Figure 3.
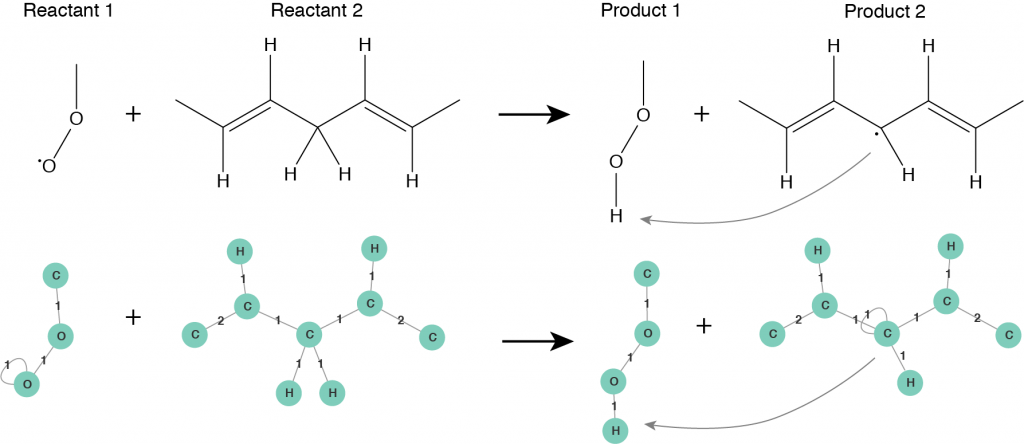
Figure 3: Reaction rule for hydrogen abstraction reaction defined in terms of patterns: Reactant 1 and Reactant 2 are the reactive patterns that will be recognized in molecular graphs and substituted by corresponding Product 1 and Product 2 patterns.
To apply a certain transformation, a pattern of a reactant has to be identified in the molecular graph of a candidate molecule by solving a subgraph isomorphism problem. Then, the list of atoms and the adjacency matrix that correspond to the pattern of a reactant, are substituted by the corresponding list of atoms and the adjacency matrix of a pattern of the product. In this way we reconstruct a new molecular structure, and a new molecular graph accordingly, that correspond to the product of the reaction. Pattern notation is very helpful and efficient when the molecule is quite big in size. Defining the patterns and the reaction rules is done manually and requires chemical expertize. In other words, it is one of the ways to program chemical reactions.
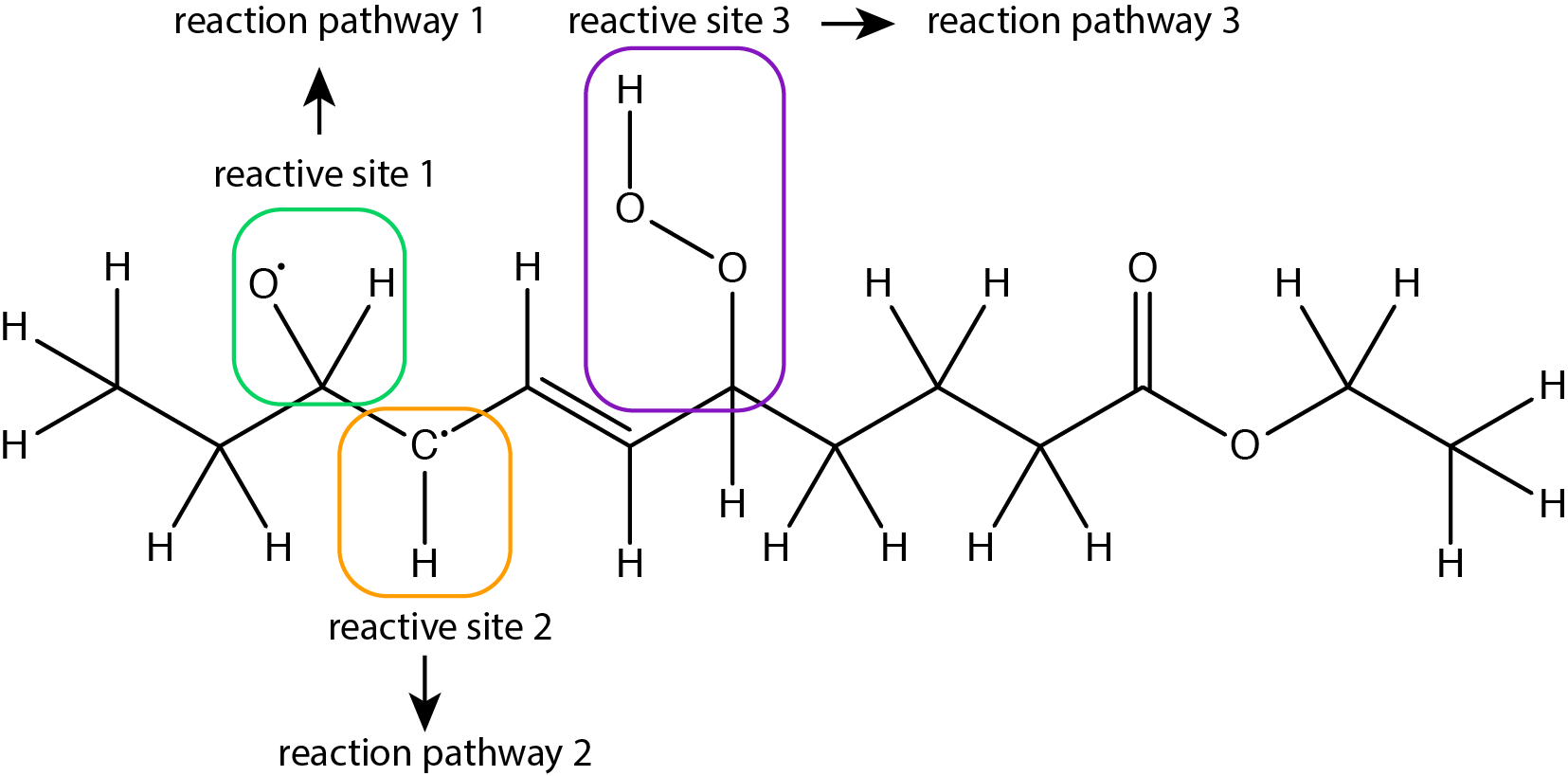
Figure 4: Example of a molecule with several reactive sites that can independently undergo different reaction pathways.
Let's take a breath to summarise the main ideas until this point, we defined molecular graphs and patterns, which correspond to reactive sites in a molecule. These reactive sites undergo transformations during the various steps of a chemical reaction and in the end we obtain a final product. Understanding the individual transformations happening at each reaction step boils down to solving a subgraph isomorphism problem. The pattern in the reactant molecule has to be isomorphically transformed to a pattern in the product molecule.
It is natural to ask whether it is possible to keep track of all the intermediate steps in a chemical reaction mechanism using the ideas presented until now. This is exactly what we describe in the remaining of this article!
We start with the initial configuration of the molecule of interest, represented as a molecular graph, and let it undergo changes following the reaction rules. Every time a molecule undergoes a transformation, the new structure is saved as an intermediate product of the reaction mechanism. As the reaction goes on, the intermediate products can also undergo transformations following the reaction rules till the final product is obtained. In this way, we are able to automatically recover all possible intermediate and product molecular states from a predefined reaction mechanism.
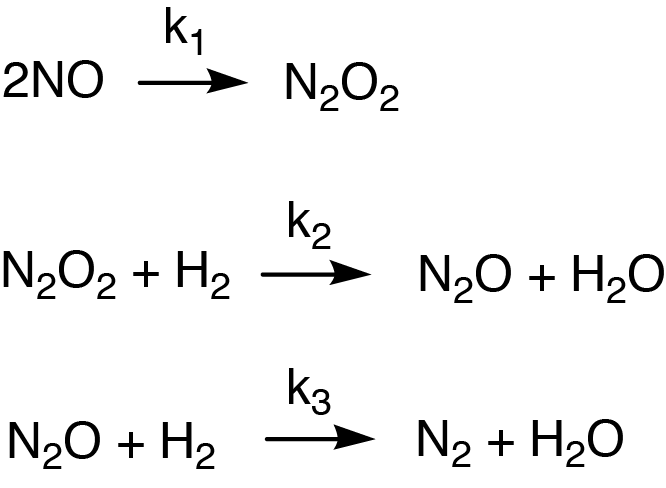
Figure 5: Example of a reaction mechanism that happens in 3 steps and involves intermediate products
We immediately observe that in order to keep track of all the reaction steps we first need an efficient representation of the whole reaction mechanism. To achieve this, chemists defined reaction networks. Roughly speaking, a reaction network describes how a molecule transforms in the various reaction steps until the final product is obtained. It's a systematic way to represent complex interaction mechanisms.
We now have a look at the formal and more general mathematical definition: a reaction network is a bipartite labeled directed graph with two types of nodes: molecular states (reactant or product) and reactions. Molecular states are connected to each other through reactions. An edge coming from a reactant state points towards a reaction node. An edge from a reaction node points towards a product state. Molecular state nodes usually have weights corresponding to their concentration. Crucial in understanding these intermediate steps of a reaction are the rates (or the frequencies) at which they occur. These rates are measured experimentally or come from quantum calculations of energy barriers of a reaction, but this topic is above the scope of this article. For this reason reaction nodes have weights corresponding to the rate coefficient of the reaction. This description is illustrated with a simple reaction in Figure 6 below.
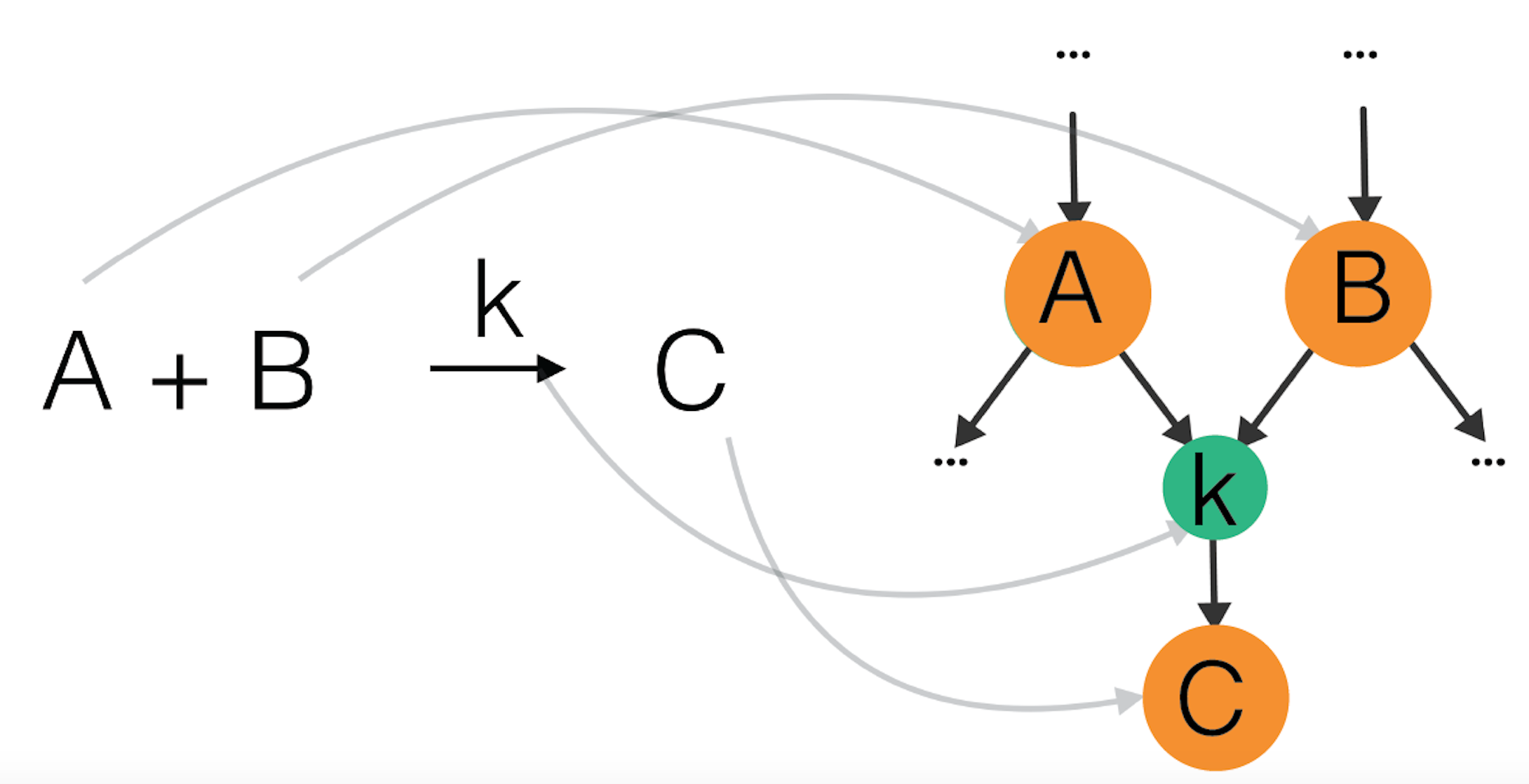
Figure 6: Example of a reaction A+B -> C as part of a reaction network: A and B are reactants, they point to a node corresponding to a reaction with rate coefficient k, which points to a product C.
To conclude, we have defined molecular graphs as a means to represent molecules. Molecular graphs allow us to "program chemistry", in the sense that we can keep track of all the intermediate products that are produced during a chemical reaction. In every step the pattern in the reactant molecule has to be isomorphically transformed to the pattern in the product molecule. Finally, the complicated reaction mechanisms, involving all the intermediate steps and products, can be represented and studied using reaction networks.
These methods make it possible for experts to deal with large chemical systems, such as metabolic processes, protein-protein interactions, pyrolysis, lipid oxidation or any other reaction mechanisms that involve big numbers of molecular species and is challenging to handle in a manual manner.
Yuliia Orlova is a PhD student at the Computational Chemistry Group of the Van 't Hoff Institute for Molecular Sciences in the University of Amsterdam.
The featured image used for this article is from:
H. Jeong, S. P. Mason, A.-L. Barabási, Z. N. Oltvai, Lethality and centrality in protein networks, Nature 411, 41-42 (2001).
Since 2016 the world has been witnessing the Rohingya genocide in Myanmar, in 2021 we all saw the Capitol riots on tv. What do networks have to do with these events?
At this very moment, the emergent science of DNA self-assembly is giving birth to a new field of mathematics that might be called DNA-mathematics. Cleverly constructed DNA molecules will self-assemble into pre-determined complex structures when placed in solution together.
In times of war, secure communication can be the difference between life and death, or even winning or losing a war. The first to patent a rotor machine in Europe was Arthur Scherbius in 1918. Scherbius’ version of the rotor machine became a commercial success, unlike the other patented machines. Scherbius named his machine Enigma.
Percolation theory is a branch of mathematics at the interface between probability theory and graph theory. The term 'percolation' originates from materials science. A representative question is as follows. Suppose some liquid is poured over a porous material. Will the liquid be able to make its way from hole to hole and reach the bottom?
A mathematician once told me that problems that are very simple to state can be very deceiving, and sometimes turn out to be extremely difficult to solve. One such problem was the Four Color Problem.
