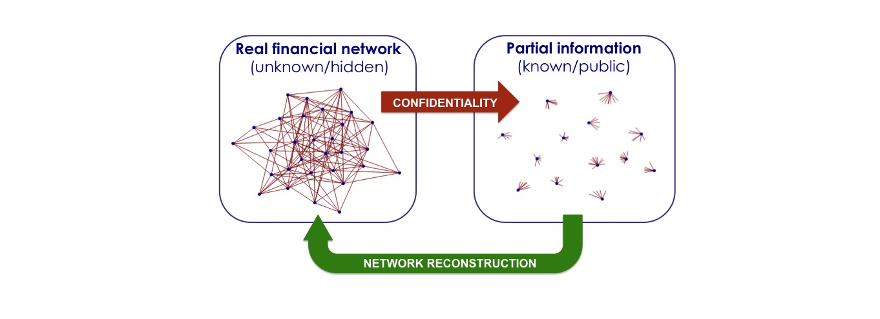
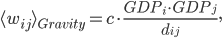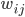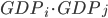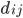A complete overview of interbank exchanges would help prevent a new financial collapse. However, banks do not provide this information: this is why a “network reconstruction” methodology to infer the unobserved connections is needed.
Over the last 20 years, the popularity of the so-called theory of complex networks has been steadily rising. Initially started by a small but fast-growing community of (mainly) statistical physicists, network theory has rapidly extended across several scientific disciplines. The success of the theory lies in the ability of defining, measuring and modelling a number of properties that characterize several real-world networks. An area where the theory of complex networks has proven to be very successful concerns the analysis of financial relations between banks.
A strong impulse for looking at this kind of financial relations through the lens of the theory of complex networks came from the financial crisis of 2008. That event dramatically illustrated that banks are intertwined in a complex, global web of loans and other exposures. In this network, a bank is represented as a node and a loan received by bank A from bank B is represented as a directed link pointing from A to B (see figure). Besides the mere existence of a link, the intensity or weight of that link (quantifying how big the loan is) is clearly important. The web of all financial exposures among banks is the crucial means of propagation of instabilities: if a bank defaults, in general it will not be able to repay its debt towards the banks it borrowed money from, thereby triggering a potential secondary wave of defaults involving those banks (a mechanism known as financial contagion). In simple words, if an unstable bank A has borrowed money from bank B, which in turn has borrowed money from bank C, then bank C can potentially become unstable as well, due to the (indirect) effect of bank B inheriting bank A’s instability and propagating it to bank C.

In an interbank network, the nodes represent all banks in a given portion of the banking system. These nodes are connected by directed links, i.e. links that have a specific orientation, which can be represented by an arrow. Conventionally, an arrow from bank A to bank B means that bank A has borrowed money from bank B. In this situation, bank B is exposed to the potential default of bank A. If such a default happened, a shock would propagate from A to B. Each link can be assigned a weight representing how big the exposure is, i.e. how much money has been lent.
Ideally, in order to quantify the risk and expected impact of financial contagion, one should map out the detailed structure of the interbank network and use it to stress-test the banking system, i.e. consider potential shock scenarios and work out the consequences via mathematical models and numerical algorithms.
However, a detailed map of the interbank network is empirically inaccessible. Indeed, according to the current banking regulations, financial institutions are not required to publicly disclose information on whom they lend to and borrow from, but only on their aggregate debt (the so-called total liabilities) and credit (the total assets). As we will discuss below, the knowledge of total assets and total liabilities is not enough in order to correctly figure out the link density and other topological properties of the network, which are however essential in order to reliably estimate the risk of financial contagion and, ultimately, the stability of the system.
Link Density
The link density in a network is defined as the total number of links within the network, divided by the maximum possible number of links. It gives an indication of how likely it is that two banks of the network are connected, through loans, to each other.
Low link density
There are not so many connections in the network which means that banks don't have transactions with many other banks.
High link density
There are many connections in the network which means that many banks have transactions with many other banks.
This circumstance prevents us from figuring out how vulnerable our banking system actually is and from characterizing the likelihood of events like the propagation of shocks and the onset of cascading failures. Quantitave research on financial networks helps thus in the investigation of possible effective revisions of present-day disclosure rules.
Reconstruction of the interbank network
A potential solution to the problem of data inaccessibility comes from the possibility of statistically reconstructing the interbank network from the available pieces of empirical information. Several network reconstruction techniques have been developed with the aim of inferring the unknown structure of a network (along with its link weights), given only partial knowledge. The closer the output of a reconstruction method is to the actual interbank network, the more effective the banking regulatory and supervisory measures exploiting that method can be made.
The picture is taken from a press release of Leiden University
Research in network reconstruction found that the knowledge of the aggregate information disclosed by banks is not, by itself, enough to guarantee a reliable reconstruction of the whole network. For instance, the link density (i.e. the total number of links within the network, divided by the maximum possible number) cannot be directly retrieved only from this piece of information. Still, as recent research has pointed out, the reconstruction algorithms that come closer to the actual density provide a much more accurate estimate of the systemic resilience to financial shocks than the algorithms that systematically over- or under-estimate it.
In the second part of this article the most successful reconstruction method that exists today, the entropy-based reconstruction method, is discussed in detail. In an investigation carried out by several central banks it was judged that this model is the best probabilistic model for reconstructing the interbank network.
PART II - Details on the reconstruction method
The maximum-entropy principle
Currently, the most successful reconstruction method is based on the principle of maximum entropy and can be illustrated as follows. If we represent the unobservable (weighted, directed) interbank network as an  asymmetric square matrix
asymmetric square matrix 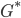 with non-negative real entries, then the empirically accessible information (the total assets and total liabilities mentioned above) is represented by the margins, i.e. the sums over the rows and columns, of the matrix itself. Let us explicitly stress that, while the available information is encoded into the knowledge of these
with non-negative real entries, then the empirically accessible information (the total assets and total liabilities mentioned above) is represented by the margins, i.e. the sums over the rows and columns, of the matrix itself. Let us explicitly stress that, while the available information is encoded into the knowledge of these 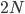 numbers, the number of entries of
numbers, the number of entries of 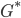 to be estimated is of order
to be estimated is of order 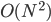 . Strictly speaking, this operation is technically impossible. However, from an inferential point of view, one may look for a probabilistic recipe that is optimal, i.e. that leads to the most reliable estimate of the original network. Put simply, the probabilistic problem is the following: given the margins, how can we best reconstruct the whole network? What should we select as the best probability distribution over the space of candidate networks?
. Strictly speaking, this operation is technically impossible. However, from an inferential point of view, one may look for a probabilistic recipe that is optimal, i.e. that leads to the most reliable estimate of the original network. Put simply, the probabilistic problem is the following: given the margins, how can we best reconstruct the whole network? What should we select as the best probability distribution over the space of candidate networks?
Statistical physics has a long tradition in solving problems of this kind. When describing systems with a large number of constituents for which there is no complete microscopic information available, statistical physics looks for a probabilistic description that only requires the knowledge of certain macroscopic “constraints” (typically, the conserved physical quantities in the system, such as total energy and total number of particles). This description is achieved by looking for the probability distribution (over the unobserved microscopic states) that maximizes the so-called Shannon entropy. In simple words, maximizing the entropy corresponds to honestly stating that we should minimize our certainty (i.e. maximize our uncertainty) about the unobservable properties of the system: except for the information we do have about the observable macroscopic constraints, we should be maximally agnostic about the system’s properties. The constrained maximization of the entropy leads to the most unbiased probability distribution over the possible states of the system.
Shannon entropy
It is defined as 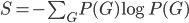 where
where 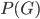 is a probability distribution over a set of states and the sum runs over all such states. It was first proposed by Gibbs who put it at the foundation of his theory of ensembles . Later, it was axiomatically derived by Shannon who looked for a quantity able to quantify the uncertainty associated with a probability distribution . Shannon entropy attains its maximum for a uniform distribution, a result indicating that the maximally uncertain situation is the one where no state is more probable than any other. On the other hand, when we know that there is a number W of equally viable states, while all other states are impossible, Shannon entropy reduces to Boltzmann entropy, defined as
is a probability distribution over a set of states and the sum runs over all such states. It was first proposed by Gibbs who put it at the foundation of his theory of ensembles . Later, it was axiomatically derived by Shannon who looked for a quantity able to quantify the uncertainty associated with a probability distribution . Shannon entropy attains its maximum for a uniform distribution, a result indicating that the maximally uncertain situation is the one where no state is more probable than any other. On the other hand, when we know that there is a number W of equally viable states, while all other states are impossible, Shannon entropy reduces to Boltzmann entropy, defined as 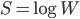 .
.
In our network reconstruction problem, the unobservable microscopic state is the set of all links (along with their weights) of the financial network (i.e. the full matrix 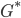 ), the macroscopic constraints are the observed margins of the matrix, and the entropy maximization procedure leads to our best guess for the probability
), the macroscopic constraints are the observed margins of the matrix, and the entropy maximization procedure leads to our best guess for the probability 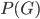 that a candidate network
that a candidate network 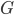 is the correct network
is the correct network 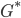 .
.
A quick look at the old model
Before discussing the output of the maximum-entropy reconstruction method, we note that its probabilistic nature is one of the key differences with respect to most alternative “greedy” algorithms, which are intrinsically deterministic.
For instance, one of the frequently used traditional methods, based on the so-called Capital-Asset Pricing Model (CAPM), estimates the weight of the link from, say, Rabobank to ING by multiplying Rabobank’s total liabilities by ING’s total assets and dividing by the total money in circulation in the system. For a generic pair of banks  and
and 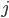 , the CAPM predicts that the weight of the link from bank
, the CAPM predicts that the weight of the link from bank  to bank
to bank 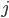 is
is
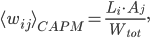
where 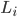 denotes the total liabilities of bank
denotes the total liabilities of bank  and
and 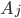 denotes the total assets of bank
denotes the total assets of bank 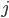 .
. 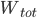 represents the total amount of money within the system and can be calculated as the sum of the total assets or total liabilities of all banks in the network, i.e.
represents the total amount of money within the system and can be calculated as the sum of the total assets or total liabilities of all banks in the network, i.e.
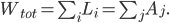
The chosen expression for 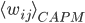 ensures that the empirical margins are correctly replicated: after summing over
ensures that the empirical margins are correctly replicated: after summing over 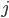 , one retrieves a value of the reconstructed total liabilities of bank
, one retrieves a value of the reconstructed total liabilities of bank  that equals the empirical value
that equals the empirical value 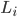 . Similarly, summing over
. Similarly, summing over  yields a value for the reconstructed total assets of bank
yields a value for the reconstructed total assets of bank 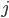 that is equal to the empirical value
that is equal to the empirical value 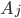 .
.
However, this procedure creates a network where all banks are connected with each other, in contradiction with the empirical fact that the majority of relations are non-existent, i.e. that the link density is very low. As a consequence, the few actual connections are much heavier than predicted by the old model, which therefore necessarily underestimates the chance of financial contagion through those links.
The estimation of weights based upon the CAPM can be regarded as a version of the well-known gravity model prescription (see box below). The gravity model works remarkably well when estimating the intensity of the realized (i.e. positive-weight) links of several economic, financial, and even social networks. For this reason, it is well established in economics. However, just like the CAPM, it has the main limitation of predicting a fully connected network, in contrast with the nontrivial properites of real networks highlighted by more recent research.
The entropy-based reconstruction model
We can now briefly explain the outcome of the maximum-entropy network reconstruction method. Just like the CAPM, the accessible empirical information is assumed to be the total assets 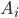 , and total liabilities
, and total liabilities 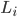 of each bank
of each bank  in the system. In principle, one could therefore use those
in the system. In principle, one could therefore use those 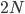 quantities as constraints and directly maximize the entropy. However, it turns out that this procedure would result in a probability
quantities as constraints and directly maximize the entropy. However, it turns out that this procedure would result in a probability 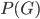 that is mostly peaked over very dense, almost fully connected networks. Therefore, although this outcome is probabilistic, it suffers from the same limitation of that of the CAPM.
that is mostly peaked over very dense, almost fully connected networks. Therefore, although this outcome is probabilistic, it suffers from the same limitation of that of the CAPM.
A crucial improvement comes from realizing that, if one had access to the numbers of incoming and outgoing links (the so-called in-degree and out-degree) of each bank, then one could use those as constraints in the entropy maximization phase. By construction, this procedure would produce networks with the same (expected) in- and out-degrees as the real network. As a result, the link density would be correctly replicated, along with several higher-order properties that turn out to be well reproduced in that case. Unfortunately, the in- and out-degrees are in fact not empirically accessible, due to the confidentiality issues mentioned above. However, it has been found that, empirically, the total assets and total liabilities of each bank can be used to preliminarily estimate the in- and out-degrees, using precisely the mathematical expression that the maximum-entropy method predicts when ideally using the degrees themselves as constraints. The final result is rather simple and consists of two steps, the first one establishing the probability of existence of each link and the second one establishing the weight of the realized links.
In the first step, a directed link from node  to node
to node 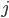 is placed with a connection probability given by
is placed with a connection probability given by
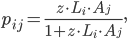
where the free parameter  can be tuned to reproduce the desired link density. This is done by choosing the unique value of
can be tuned to reproduce the desired link density. This is done by choosing the unique value of  such that the average of the connection probability over all pairs of nodes equals the empirical link density. Although the latter may not be known for the specific network under investigation, it turns out that several interbank networks have link densities of comparable value, thereby allowing
such that the average of the connection probability over all pairs of nodes equals the empirical link density. Although the latter may not be known for the specific network under investigation, it turns out that several interbank networks have link densities of comparable value, thereby allowing  to be tuned in order to replicate such empirical value.
to be tuned in order to replicate such empirical value.
In the second step, the weight of a link that is successfully established from node  to node
to node 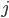 is set equal to
is set equal to
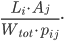
This choice ensures that the expected link weight is the same as in the CAPM, and consequently the expected total assets and total liabilities of each node are still equal to the corresponding empirical values. Crucially, while the expected link weight is the same as in the CAPM, the typical realizations of the network are much sparser, due to the realistic expected link density.
In extreme summary, the probabilistic recipe is:
“any two banks establish a connection whose weight is 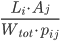 with probability
with probability 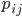 and no connection with probability
and no connection with probability  ”
”
It has been shown that the above model replicates a number of network properties satisfactorily and consequently allows for a reliable estimate of systemic risk from the observed partial information. In the figure below we show an application of this reconstruction method to a snapshot of the Italian electronic market for interbank deposits eMID, i.e. the network whose nodes are banks and whose generic link  represents the loan granted from bank
represents the loan granted from bank  to bank
to bank  .
.
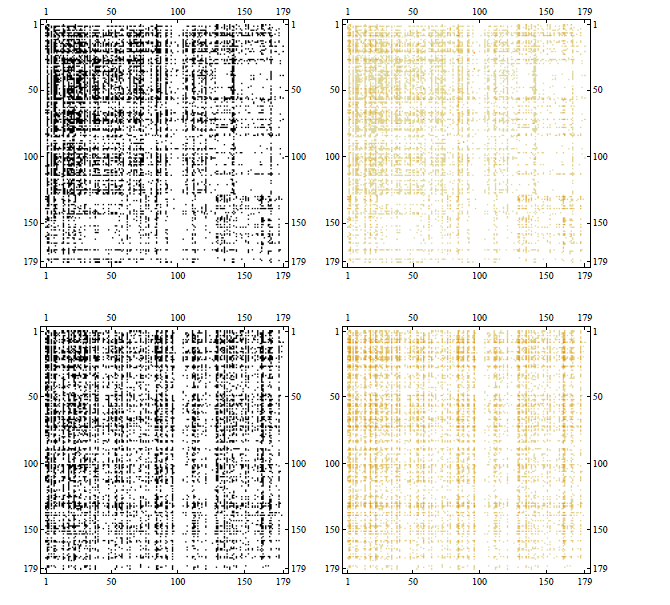
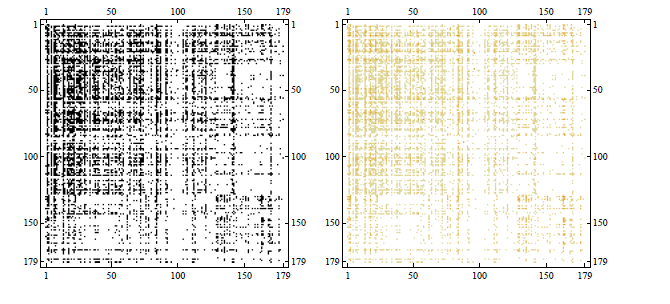
Comparison between the observed adjacency matrix of the eMID network in 2003 (top panels) and its reconstructed version (bottom panels). Left panels represent binary adjacency matrices with black/white denoting the presence/absence of connections, whereas, right panels represent weighted adjacency matrices with color intensity denoting the weight of connections.
A refined implementation of the method, further improving the probabilistic structure of the reconstructed link weights and enhancing the fit to real networks, has been published very recently.
The quest for the “best” reconstruction model
Recently, several “horse races”, i.e. studies aimed at comparing the performance of alternative methods in reconstructing real interbank networks, have been run independently by research groups who had special access to different “entire” networks. The entropy-based model described here has been found to systematically outperform competing methods.
We finally note that, also in the current Corona crisis, reliably estimating the economic effects of the lockdown and of the possible recovery interventions would require the knowledge of the entire network of business relationships (supply chains) among firms. Unfortunately, similar to the interbank case, the structure of this network is privacy-protected. Therefore there is an increasing need for network reconstruction techniques that give reliable outputs in absence of complete information, not only for the benefit of financial regulation but also to improve economic forecasting and policy making.