Evolutionary algorithms help physicians in the Amsterdam UMC to make treatment plans for prostate cancer patients.
Cancer is a disease in which cells grow and divide abnormally and form a tumor. Cancer cells can invade or spread out to other parts of the body, and when they do so, they interfere with body functions that are necessary to live. A common form of cancer among elderly men is prostate cancer. The prostate is a walnut-sized gland located close to the bladder and the rectum, and is part of the male reproductive system. There are different effective treatments for prostate cancer. Which treatment is best depends on the stage of the disease, but also on the preferences of the patient, as each treatment has potentially different undesired side effects.
A commonly applied treatment against cancer is radiation therapy. In radiation therapy, or radiotherapy, ionizing radiation dose is delivered to the cancer cells. One form of radiotherapy that is applied in the treatment of prostate cancer is brachytherapy. In brachytherapy, about ten to twenty catheters (hollow tubes) are surgically implanted into the tumor. A machine can then guide a small radioactive source through the catheters. This radioactive source is about the size of a rice grain, and is made of iridium. The source is stopped at different positions into the catheters and emits radiation there. The radiation causes damage that kills tumor cells or slows their growth. Prostate cancer cells, like many other cancerous cell types, are more sensitive to radiation than healthy cells. This yields the possibility to kill cancerous cells, without killing surrounding healthy cells. However, radiation from the source spreads out in all directions , which makes it impossible to maximally irradiate the tumor (which is called tumor coverage) while fully preventing radiation dose to surrounding healthy organs (which is called organ sparing).
To effectively treat a patient with brachytherapy, a good trade-off between these two conflicting objectives needs to be found.
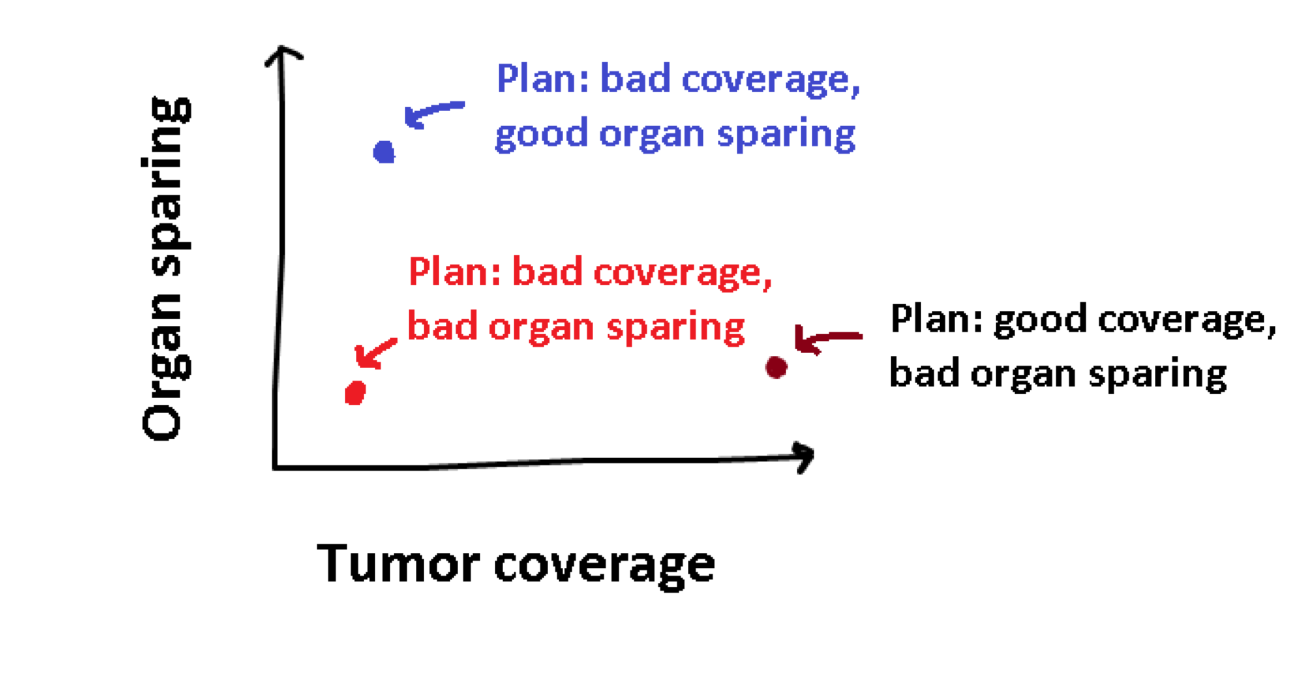
Treatment planning is the process of determining how the patient should be treated, by adapting the time that the radioactive source stops at each position in the implanted catheters. For each treatment plan, we can calculate how good it is at tumor coverage, and how good it is at organ sparing. We can visualize this as follows:
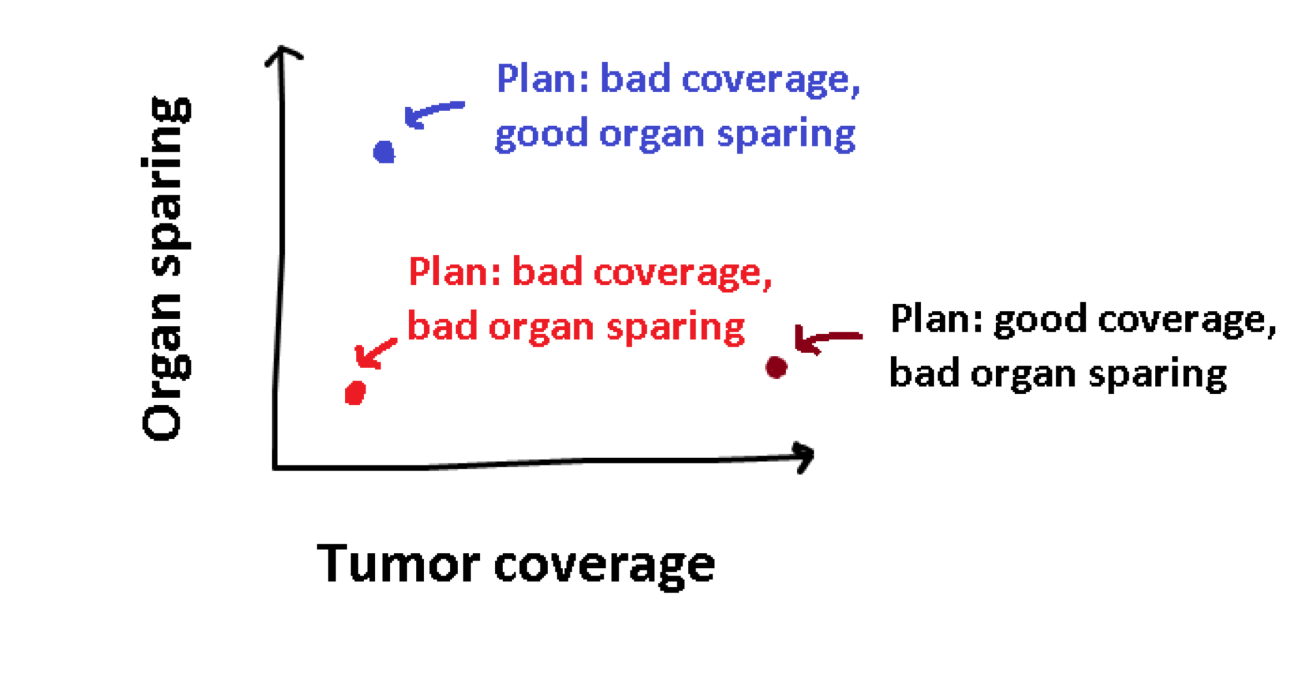
The plan in red is rather obviously a bad plan, as the other plans have better values for both objectives. However, the plan in blue is not better than the black one, or vice-verse, they are just different. This concept of superiority or optimality with multiple objectives is called Pareto optimality. Multi-objective optimization problems do not have a single optimum, but a set of Pareto optimal solutions. When there are two objectives, as in the case of treatment planning, we can visualize this set as a trade-off curve:
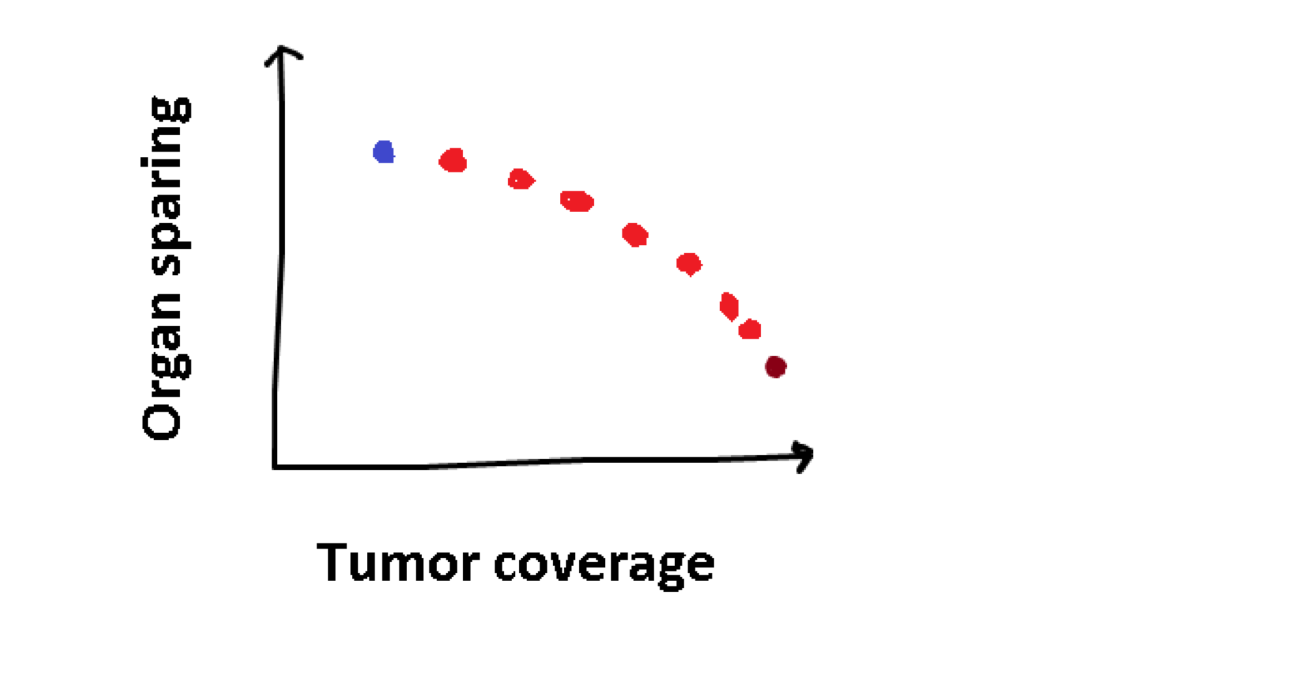
This trade-off curve shows different possible treatment plans, and how they trade-off the two objectives, which is different for every patient. Using this visualization, the best treatment plan can be selected for the patient. However, a question we did not cover yet is how can we obtain these treatment plans that make up the trade-off curve?
Evolutionary algorithms
Practical optimization problems are often difficult to analyze, for example because they rely on data, simulations, or proprietary software. This makes it hard to gain a sufficient understanding of the internal structure of the problem that is required to apply mathematical optimization algorithms. To still be able to solve the problem, a metaheuristic can be employed. Metaheuristics are search algorithms that can be applied without assuming any problem-specific knowledge, that is, they assume the problem to be a black box. They are however, as the name implies, heuristics, meaning that there are typically no guarantees of finding the optimal solution. Metaheuristics are interesting when a good solution is needed rather fast, and when it is not that important that this solution is (provably) optimal, which is often the case in practice.
Evolutionary Algorithms (EAs) are black-box optimization algorithms that are particularly well-suited for multi-objective optimization. EAs can be roughly described as inspired by Darwin's theory of evolution, and borrow a lot of terminology from the field of biology. EAs maintain a population of solutions that is simultaneously improved over the course of multiple generations. The best solutions in the population are selected, to produce an offspring. Just like survival of the fittest.
A commonly used approach to generate an offspring in numerical optimization, where the to-be optimized variables are real-valued, is via sampling. A probability distribution models high-fitness regions in some decision space, which is adapted over time by combining information from high-quality solutions, and is used to sample new solutions from. A method that equips such a probability model is also known as Estimation of Distribution Algorithm (EDA) or Model-Based EA (MBEA). An illustration of how such an algorithm works, in this case a Gaussian-based EA, is given below:
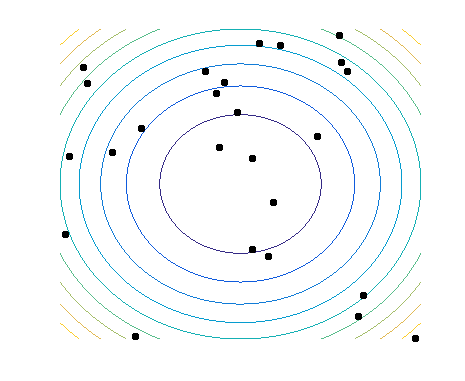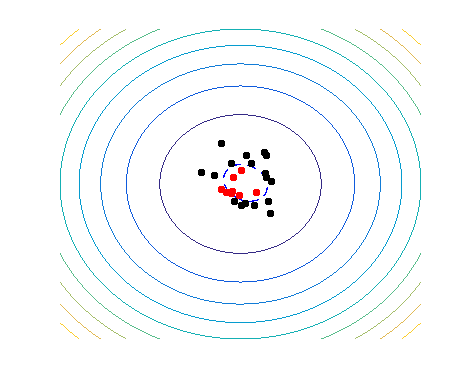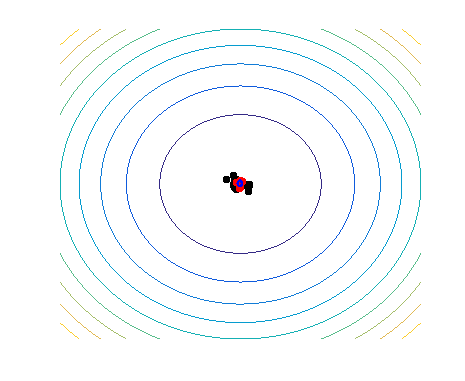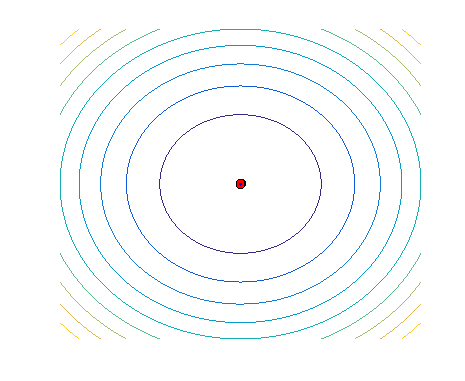
This animations shows a simple single-objective optimization problem known as the sphere problem, in which the optimum is in the middle of the contour lines. Each generation of an MBEA consists of three steps:
select the best solutions in the population (i.e. points closest to the center);
fit a probability distribution to the selected solutions;
sample a new population of solutions from the probability distribution.
If you would like to read more on (the mathematics behind) MBEAs can have a look at the Covariance Matrix Adaptation Evolution Strategies (CMA-ES) and the Adapted Maximum-Likelihood Gaussian Model EA (AMaLGaM).
Evolutionary algorithms are naturally well-suited for multi-objective optimization, as they already maintain a population of multiple solutions to guide the search. What remains is to promote some form of diversity upon this population in order to obtain solutions with different trade-offs.
Back to the patient…
While EAs can be applied to problems out of the box, there can be great benefit from adapting the algorithm to the problem at hand, for example to speed up the process. This is known to as grey-box optimization, in which some details about the problem are known, but not enough to be able to apply mathematical optimization algorithms. By exploiting problem-specific knowledge of the brachytherapy problem, the MO-GOMEA (for further reading)algorithm can obtain high-quality trade-off curves within a minute, for a deeper look into this topic you can have a look in this article or this one.
When MO-GOMEA was applied on data of patients previously treated in the Amsterdam UMC, location AMC, in Amsterdam, the Netherlands, it became clear different patients can have very different trade-off curves (for more details we refer to this article), this can be seen on the figure on the right. The two axis here still represent tumor coverage and organ sparing, which are quantified using the Least Coverage Index (LCI) and Least Sparing Index (for details, see). Each dot represents a treatment plan with a different trade-off, and different colors represent different patients.
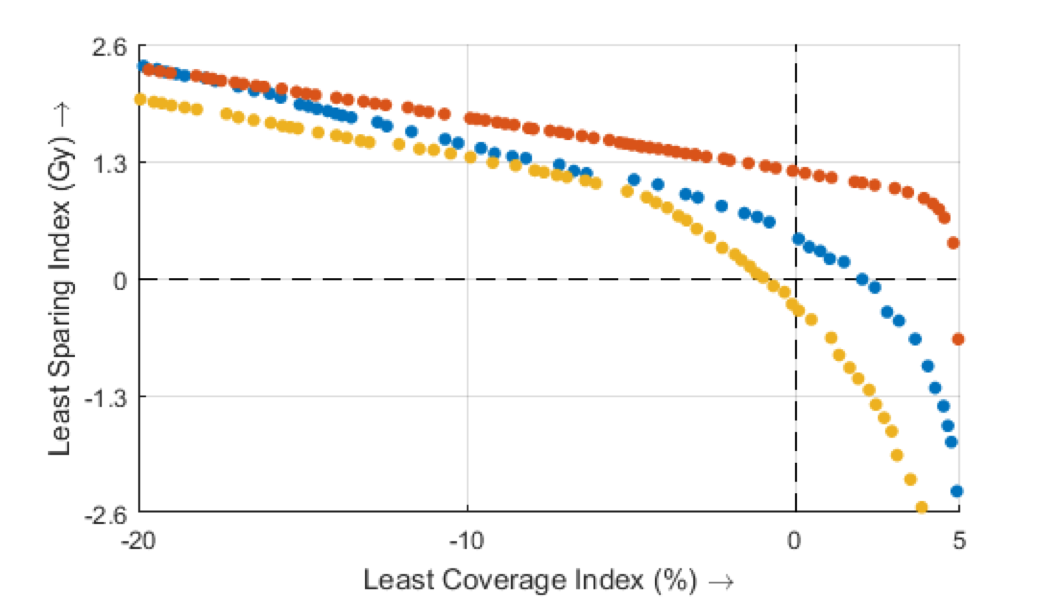
The ideal treatment plan would be in the upper right corner. This figure shows that the patient in red clearly has a more favorable anatomy or tumor position, as it is possible to obtain at the same time a better (higher) coverage and better (higher) sparing, compared to the other two patients. Using visualizations like these, the physician gains insight in the patient-specific trade-offs, which can then be used to select the best plan for the patient. This insight in the possible trade-offs is the big advantage of multi-objective optimization.
The quality of the treatment plans as obtained with MO-GOMEA was compared to the plans that were actually used to treat the patient with (see here for more details). These clinical plans were manually constructed by a physician or clinician. Graphical tools are available to aid in this process, but these tools work on a trial-and error basis. The planner makes an adaptation to the plan, and inspects whether the result is as desired. By making many small adaptations, the treatment plan is adapted to the anatomy of the patient, which takes up to 30 minutes or more. This manual optimization process was recorded, and after each adaptation, the quality of the plan was recomputed. The process can be visualized in the same trade-off figures as we saw before:
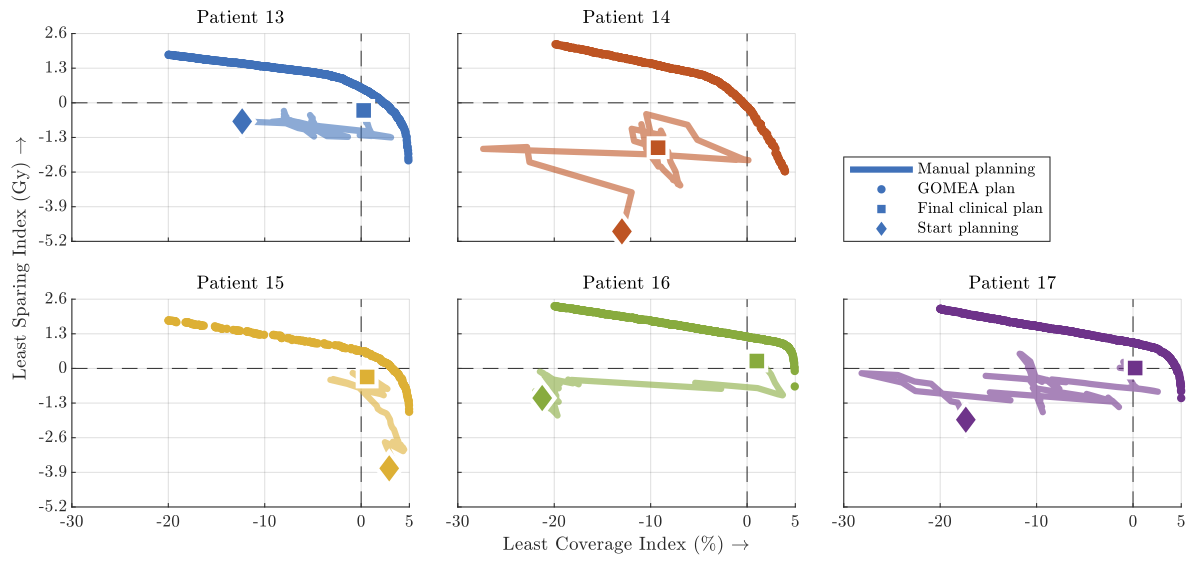
The zig-zag line you see here shows the quality of the treatment plan as it was made by the physician. It starts with the diamond-shaped marker, and as changes are made, the plan quality changes, until all the way in the end, which is indicated by the square. For patient 17 for example, you clearly see that the final plan (square) is better than the initial pan (diamond), so the physician did a good job. But what you also see is that the process took many steps. The zig-zags in the line also showed that sometimes bad changes where made as well. The tick curved-line is actually a lot of single dots, which are the plans that are obtained automatically using our evolutionary algorithm. These are much better that the manually obtained plans, and do not require any manual effort at all. When we asked physicians to choose between their manually constructed plan and automatically generated plans, without telling them which is which, they chose for the automatically generated plans in 98% of the cases!
This research showed that multi-objective optimization is a very effective approach to treatment planning of brachytherapy for prostate cancer and gives physicians new insights on how to better treat prostate cancer patients. As a result, as of spring 2020, it is used in the Amsterdam UMC to generate treatment plans for prostate cancer patients.
Acknowledgements
This article is based on research performed at the Amsterdam UMC, location AMC, and the Centrum Wiskunde & Informatica (CWI), and was funded by the Dutch research council (NWO) and Elekta Brachytherapy, Veenendaal. This article is based on Stef’s PhD thesis titled “Model-based evolutionary algorithms for finding diverse high-quality solutions”.
It is quite difficult to extract information from your body. Your body is so vast that millions upon millions of messages get sent and deleted every second. It is impossible to know exactly who said something. The doctor’s main challenge is finding a way to reconstruct the network of interacting cells given the limited information she can measure.
How can one hope to understand the precise structure of a virus if it is able to become unrecognizable within weeks? The mathematics behind this questions didn't let go of my mind for extensive periods of time during my PhD studies in Belgium.
On a quiet afternoon, professor Meth is working in her office in Leiden on some tantalizing mathematics problems. Suddenly, someone knocking on her door nervously disrupts the silence.
After having a near-fatal accident falling off his horse, Prussian footman Hans Berger (1873—1941) was surprised to learn that his sister had—being kilometers away—him a telegram to let him know that she sensed he was in grave danger.
