Congested road networks are a big problem in many countries. Building more roads is not always the best solution to solve this issue. One of the reasons for this is that drivers behave selfishly (trying to have the shortest possible travel time to get from work to home), which leads to inefficient usage of the road network as many drivers want to use the same parts of the network.
An example of this phenomenon, called Pigou's network, is given in this article. Tolling schemes are a way to enforce selfish drivers (equilibrium flow) adopt a driving behavior which decreases the average travel time of all drivers (social optimal flow)!
In the preceding article we showed how tolls (or taxes) can be used to mitigate the effects of selfish routing in Pigou's network. In particular, we computed tolls with the property that if players minimize a combined cost of latency and toll, the resulting equilibrium flow is precisely the socially optimal flow. This means that the network is being used efficiently. Do such tolls always exist? We only showed this for one pair of latency functions, but what about arbitrary latency functions? This question has been answered affirmative by Beckmann, McGuire and Winston ![[1]](https://www.networkpages.nl/wp-content/plugins/latex/cache/tex_35dba5d75538a9bbe0b4da4422759a0e.gif) already back in 1956. This was a couple of years after the introduction of Wardrop's routing model
already back in 1956. This was a couple of years after the introduction of Wardrop's routing model ![[2]](https://www.networkpages.nl/wp-content/plugins/latex/cache/tex_beb4dbf9af069aa2df7b147229965085.gif) in 1952, which is a general description of the model we consider here. They showed that optimal tolls, to induce the socially optimal flow as equilibrium flow, always exist (under some mild assumptions on the latency functions)!
in 1952, which is a general description of the model we consider here. They showed that optimal tolls, to induce the socially optimal flow as equilibrium flow, always exist (under some mild assumptions on the latency functions)!
Figure 1: Toll maps in Ireland (Left panel) and France (Right panel, Photo from AboutFrance.com)
In this article we will describe how to set tolls in such a way that the socially optimal flow becomes an equilibrium flow. We do this for arbitrary latency functions that satisfy some basic assumptions. For simplicity, we focus on Pigou's network. Our goal is to give an intuitive argument for what these tolls should look like. The general result uses techniques from convex programming ![[1]](https://www.networkpages.nl/wp-content/plugins/latex/cache/tex_35dba5d75538a9bbe0b4da4422759a0e.gif) .
.
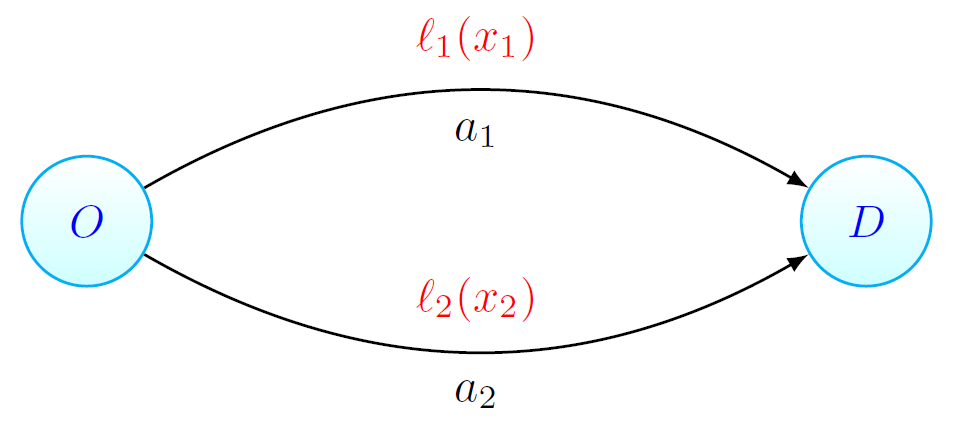
We first make some mild assumptions concerning the properties the latency functions 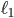 and
and 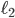 should have. As before, we assume that they are non-negative and increasing (to mimic the effect of congestion). Moreover, we also assume that both functions are differentiable.
should have. As before, we assume that they are non-negative and increasing (to mimic the effect of congestion). Moreover, we also assume that both functions are differentiable.
Remember that the social cost of a flow 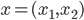 is given by the average travel time in the network, which is
is given by the average travel time in the network, which is 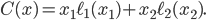 We will call
We will call 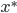 the social optimum as before. Suppose that there is a positive amount of flow on the upper road:
the social optimum as before. Suppose that there is a positive amount of flow on the upper road: 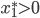 . Since the flow
. Since the flow 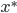 is optimal, this means that if we would shift some small amount of flow
is optimal, this means that if we would shift some small amount of flow 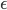 from the upper to the lower road, then the social cost of the resulting flow can't be better than the cost of flow
from the upper to the lower road, then the social cost of the resulting flow can't be better than the cost of flow 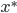 . An important concept here is the rate of change in social cost on a road, which is precisely the derivative of the term
. An important concept here is the rate of change in social cost on a road, which is precisely the derivative of the term 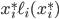 . Using the chain rule, we get that
. Using the chain rule, we get that
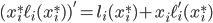
where 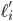 is the derivative of the function
is the derivative of the function 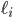 .
.
If we shift an amount of  from the upper to the lower road, then the social cost decreases by approximately
from the upper to the lower road, then the social cost decreases by approximately 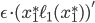 on the upper road, and increases by approximately
on the upper road, and increases by approximately 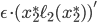 on the lower road. This approximation is valid, since
on the lower road. This approximation is valid, since 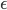 is very small. Because
is very small. Because 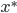 is a socially optimal flow, the increase of social cost on the lower road cannot be higher than the decrease of social cost on the upper road. Said differently, we must have
is a socially optimal flow, the increase of social cost on the lower road cannot be higher than the decrease of social cost on the upper road. Said differently, we must have 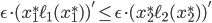 . Using the expression for the derivative given above, this is the same as saying that
. Using the expression for the derivative given above, this is the same as saying that
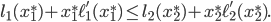
Now, let us think back of what it means to be an equilibrium flow under a tolling scheme. If we have tolls 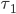 and
and 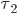 on the roads, and there is a positive amount of flow on the upper road, then the equilibrium conditions tell us that the combined cost of latency and toll on the upper road must be smaller or equal than that of the lower road. Otherwise some small fraction of flow could switch to the lower road to get a better combined cost. Stated mathematically, if
on the roads, and there is a positive amount of flow on the upper road, then the equilibrium conditions tell us that the combined cost of latency and toll on the upper road must be smaller or equal than that of the lower road. Otherwise some small fraction of flow could switch to the lower road to get a better combined cost. Stated mathematically, if 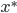 is an equilibrium for the tolls
is an equilibrium for the tolls 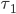 and
and 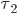 , then we must have
, then we must have
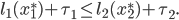
Comparing the last two inequalities, it follows that if we set
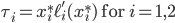
then indeed the flow on the upper road cannot get a better combined cost by switching to the lower road. We can of course use completely analogue arguments if we would use the lower road as a starting point. This shows that the tolls 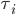 given above indeed give the social optimum as equilibrium flow for the combined cost of latency and toll!
given above indeed give the social optimum as equilibrium flow for the combined cost of latency and toll!
References
- Beckmann, M., McGuire, C.B., Winston, C.B.,: Studies in the economics of transportation. Yale University Press, New Haven (1956)
- J. G. Wardrop. Some theoretical aspects of road traffic research. Proceedings of the Institution of Civil Engineers, 1:325–378, 1952.