It is Thursday 25 of July, the clock shows 22:00, my flight with KLM lands at the international airport of Accra, the capital of Ghana. I exit from the arrivals hall of the airport and I start looking around, I see a board with my name on it, it is Francis, the director of AMI Ghana and one of the organizers of the Allotey mathematics summer school. This is how a wonderful adventure started.
We are sitting in Francis’s car driving to the hostel I am staying for a couple of nights, it is about midnight and everything is quite on the street, there is no traffic. Francis starts telling me about the summer school, how it started and the vision of the organizers. Every year math summer schools are organized in various African countries under the auspices of AMI.
African Maths Initiative (AMI) is a Kenyan NGO formed by mathematicians and mathematics educators who are working to create a stronger mathematical community and culture of mathematics across Africa in all academic levels. The inspiration to organize math camps came from Kenya, where AMI organized the first summer math camp in 2010. Nowadays various branches of AMI have been responsible for organizing such summer camps in other African countries as well. For the past nine year math camps have been organized in Kenya, Ghana, Togo (first time last summer), Rwanda (first time last summer), Ethiopia, Cameroon and Tanzania.
Since 2010 AMI has founded numerous initiatives, working closely with schools and universities. It has also inspired the creation of the UK-based charity SAMI, which continues to support and lend international expertise to projects in these countries.
That is how I got involved into this initiative, through SAMI and by two colleagues who have been participating to the program for the last three years. These math camps are organized and carried out by volunteers who all share the same passion for education and mathematics. The math we were supposed to teach doesn't need to be advanced, the basic principles of the (S)AMI math camp are that lectures should be interactive and that the whole program should be inclusive. Teachers are not supposed to lecture during a session but develop the session in such a way, using assignments, constructions, games and computer activities, such that the students find their way to the answer and explore as much as possible on their own some topic. You can think of it as some form of the Socratic method.
Discovering Euler
Participating in the Allotey Math Camp in Ghana was extremely interesting from a didactic perspective, having to prepare a mathematics session without lecturing, where the students should have the leading role, was very challenging and took much more time and energy than expected. But I must admit that the pleasure gained from the interaction and the discussions with the students during the sessions proved it was worth the effort. I had prepared two sessions and both were about geometry, about polyhedra to be specific.
The main objective of these two sessions was to present Euler’s formula for polyhedra and to prove that there exist precisely five regular solids (Platonic solids). Both sessions were developed in an interactive manner and relying on Polydron, which is a collection of plastic triangles, squares, pentagons, hexagons, octagons and decagons whose edges can be connected with each other. Using actual geometrical objects made the sessions much more interactive and the student could build objects as they pleased.
The assignment I gave was very simple, use all these polygons to construct a three-dimensional object, whichever you like the most, with the only condition that it should have no holes in it. There were various advantages using Polydron, the first was that I spared myself the difficult task of drawing three-dimensional objects on the blackboard, a task that demands quite some drawing skills.
But the most important advantage was that the students were involved in the activity. After some time they had all constructed something, a house, a tower, a football, a castle e.t.c. The next step was to count the number of points (P), the number of edges (E) and the number of faces (F) in the constructions they had made. And to compute 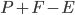of course. You wonder what the result was? For all of the constructions the formula was equal to 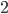! And then the important question followed, why does this happen? The complete answer to this question is not so simple and I discuss it in my other blog post found here. There are also some intuitive explanations why this formula holds but I won't spoil the fun by giving them, the time in Ghana proved that doing math is much more fun than reading the solution!
What if I tell you that long queues in airports are also caused by the impatient passengers that arrive too far in advance at the airport? Today, we will analyze how the organization of the security check queue affects the waiting time of passengers.
We might not be fully aware of it, but we all use wireless communication everyday in many familiar situations, such as when we connect our laptop to the local Wi-Fi network, when we use navigation apps to orientate ourselves while driving, or when we send a message to a friend using our smartphones. It has become so natural for the world we live in, that we often take it for granted and have no idea of how it works.
of course. You wonder what the result was? For all of the constructions the formula was equal to 
! And then the important question followed, why does this happen? The complete answer to this question is not so simple and I discuss it in my other blog post found here. There are also some intuitive explanations why this formula holds but I won't spoil the fun by giving them, the time in Ghana proved that doing math is much more fun than reading the solution!
