Have you ever wondered if you can visualise your Facebook network? And what do these networks have to do with mathematics?
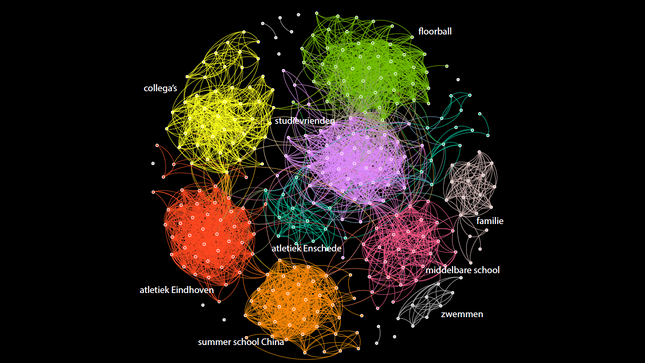
The following image shows my Facebook profile as a network: a collection of points connected with lines between them. The points are my facebook friends. Two of my facebook friends are connected with a line if they are also friends with each other.
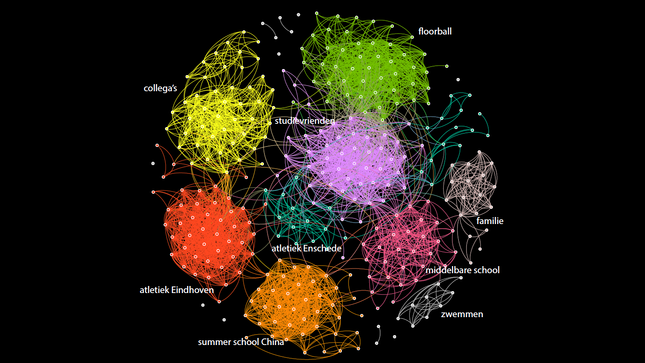
Clara's Facebook network. Made by Clara Stegehuis voor NEMO Kennislink.
Unexpected connections
It is quite nice to recollect where I met all my friends. So you can see that I have tried various sports, and that I have moved to a different city a couple of times. The people I met in a certain city often also know each other! This results into formation of groups in my network, in a specific group of people there are many connections!
But at the same time I was surprised to see that there are also quite a lot of connections between people from different groups. For example, one of my cousins knows someone from Enschede who I met at my sports club. And more surprising, someone that I met once in China knows someone from my school class!
Mathematics in huge networks
In my research I study networks, those are points which are connected with lines. The points and the lines can represent people that know each other through social media, like in the previous picture. There are many cases where the networks we study are unbelievably huge! The network consisting of my Facebook friends is rather small, "only" 317 points. But if you consider the network of all Facebook users worldwide, then you obtain a network with more that two billion points!
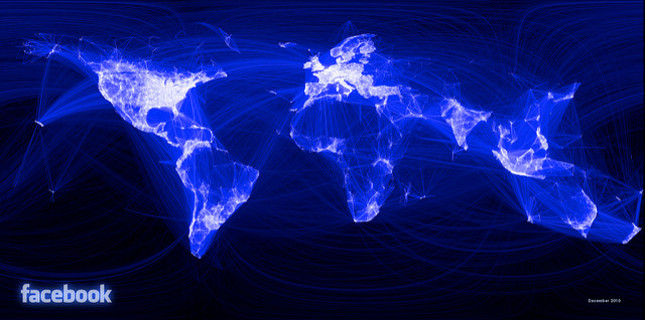
Network of all Facebook users! Made by John Haydon via Flickr CC BY-NC-SA 2.0.
Exactly because these networks are so amazingly large, it is difficult to extract useful information from them. That is why we rely on mathematics! With powerful algorithms and mathematical equations we can describe the structure and study the behavior of the network. What is surprising is that in many cases the fact that the network is so large simplifies the mathematics! With mathematical computations we aspire to learn more about large networks. For example, can we understand how a Facebook post goes viral using mathematics? And how can we identify the various groups in a network? Such questions lie at the heart of my research!
This short article is a translation of this article from my blog on NEMO Kennislink!
There are various parameters that determine whether a video will go viral or not. The content plays a role of course but who uploads the video is also important. What do networks have to do with a video going viral?
In this article Maya continues her journey from Rotterdam to Brussels. She starts thinking about a puzzle from her childhood, the three utilities problem. At the end of the jouney she has reached a very important theorem from graph theory!
A conjecture of Erdős and Hajnal from 1989 says that forbidding any specific substructure results in existence of a very large homogeneous one! In this article you will have a look into one of the most fascinating problems in modern graph theory.
